Лінійні операції над векторами
Елементи векторної алгебри
Векторні і скалярні величини
Означення 1. Величини, які цілком характеризуються їхніми числовими значеннями, називають скалярними величинами (температура, густина , об’єм та ін.).
Означення 2. Величини, які характеризуються не тільки їхніми числовими значеннями, а і напрямом, називають векторними величинами(переміщення, швидкість, прискорення, сила та ін).
Скалярні величини задаються за допомогою дійсних чисел або зображаються у вигляді точок числової осі.
Для зображення векторних величин застосовують вектори.
Означення 3. Вектором називають відрізок, що сполучає дві задані точки простору, причому зазначається, яка з них є початком, а яка кінцем. За напрям вектора вибирають напрям від його початку до кінця. Напрям вектора, як правило, позначають стрілкою, яка ставиться в кінці вектора (рис.1).
A B 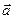
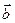
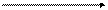 | 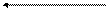 | ||||
 |
Рис. 1
Позначають вектор або однією півжирною буквою, або однією чи двома світлими буквами із стрілочкою над ними: a, 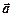 ,
, 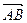 . Якщо вектор позначений двома буквами, то перша позначає його початок, а друга – його кінець.
. Якщо вектор позначений двома буквами, то перша позначає його початок, а друга – його кінець.
Означення 4. Довжину відрізка, який зображує вектор, називають модулемвектора. Модуль вектора позначають так 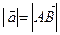 .
.
Якщо довжина вектора дорівнює одиниці, то вектор називають одиничним вектором і його часто позначають через 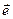 .
.
Означення 5. Вектор, початок і кінець якого збігаються, називаютьнуль-векторомі позначають 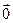 .
.
Модуль цього вектора дорівнює нулю, а його напрям невизначений.
Означення 6.Вектори, які лежать на одній прямій або паралельних прямих, називаютьколінеарними(рис. 2).


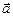
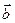
Рис. 2
Означення 7. Вектори називаються рівними, якщо вони мають рівні модулі, а напрями співпадають.
Це записують так: 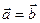 .
.
Означення 8. Два вектори називають протилежними, якщо вони протилежно направлені і мають одинакові модулі.
Це записують так: 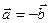 або
або 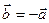 .
.
Означення 9. Вектори, які лежать в одній площині або в паралельних площинах, називають компланарними (рис. 3).
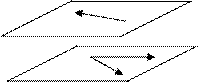 |
Рис.3
Лінійні операції над векторами
Додавання векторів.Сумою двох векторів 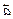 і
і 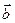 називають такий третій вектор
називають такий третій вектор 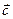 , який сполучає початок вектора
, який сполучає початок вектора 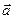 і кінець вектора
і кінець вектора 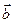 при умові суміщення кінця вектора
при умові суміщення кінця вектора 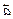 і початку вектора
і початку вектора 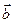 .
.
Коротко записують 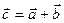 .
.
За означенням суми двох векторів випливає, що вектор 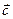 можна знайти як діагональ паралелограма, побудованого на векторах
можна знайти як діагональ паралелограма, побудованого на векторах 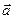 і
і 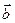 , як на сторонах (рис 4). Таке правило додавання двох неколіне арних векторів називають правилом паралелограма.
, як на сторонах (рис 4). Таке правило додавання двох неколіне арних векторів називають правилом паралелограма.



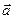
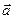
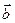




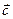 =
= 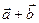
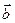
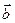
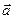
Рис. 4
Віднімання векторів. Різницею 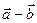 двох векторів називають такий третій вектор
двох векторів називають такий третій вектор 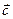 , який треба додати до вектора
, який треба додати до вектора 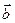 , щоб дістати вектор
, щоб дістати вектор 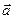 , тобто
, тобто 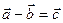 , якщо
, якщо 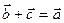 (рис. 5).
(рис. 5).




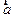

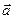
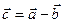
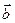
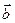
Рис. 5
Множення вектора на число.Добутком m 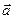 або
або 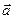 m вектора
m вектора 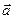 на числоm називається новий вектор, довжина якого дорівнює
на числоm називається новий вектор, довжина якого дорівнює 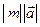 , а напрямок співпадає з напрямком
, а напрямок співпадає з напрямком 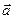 при m>0 и протилежно
при m>0 и протилежно 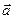 ,якщо m<0.
,якщо m<0.
Означення 10. Одиничним вектором вектора, або його ортом, називають вектор, довжина якого дорівнює одиниці і який має той самий напрям, що і даний вектор.
Довільний вектор 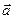 може бути представлений у вигляді добутку двох співмножників – його довжини
може бути представлений у вигляді добутку двох співмножників – його довжини 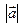 і одиничного вектора
і одиничного вектора 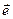 , тобто
, тобто 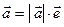 .
.
Означення 11.Два вектори, зв’язані співвідношенням 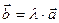 , де l деяке число, називаються колінеарними або паралельними (рис. 6).
, де l деяке число, називаються колінеарними або паралельними (рис. 6).
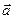
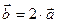
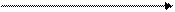 | |||
 | |||
Рис. 6
Приклад 1. Дано 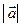 =4;
=4; 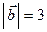 ;
; 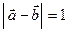 . Знайти
. Знайти 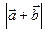 .
.

 Розв’язання. Побудуємо за правилом паралелограма
Розв’язання. Побудуємо за правилом паралелограма 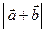 та
та 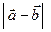 (рис.7).
(рис.7).



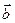
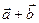
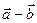
 |
Рис. 7
Використовуючи властивості діагоналей та сторін паралелограма, отримаємо: 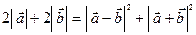 ;
; 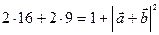 ;
; 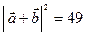 ;
; 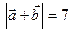 .
.
Проекція вектора на вісь
Нехай в декартовій системі координат Oxy вектор 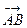 заданий двома точками A(xa; ya; za) і B(xb; yb; zb).
заданий двома точками A(xa; ya; za) і B(xb; yb; zb).
Означення 12.Проекцією вектора 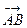 на вісь Ox називається різниця між абсцисами кінця і початку вектора
на вісь Ox називається різниця між абсцисами кінця і початку вектора 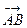 .
.
 Проекцію вектора на вісь Ox позначають прOx
Проекцію вектора на вісь Ox позначають прOx 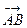 . Аналогічно визначають проекції вектора на осі Oy і Oz (рис. 8).
. Аналогічно визначають проекції вектора на осі Oy і Oz (рис. 8).






 Z
Z 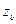


 В
В



 А
А








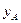
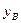 Y
Y
A’
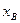 B’
B’
X
Рис. 8
Таким чином, ПРOХ 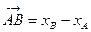 , ПРOY
, ПРOY 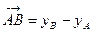 , ПРOZ
, ПРOZ 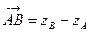 .
.
Скориставшись теоремою Піфагора можна знайти проекції вектора на площину. Наприклад, проекція вектора 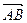 на площину XOY можна знайти за формулою
на площину XOY можна знайти за формулою
ПРXOY 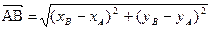 .
.
