Задания для самостоятельного решения. 1. Один из углов параллелограмма на 12°больше другого угла

1. Один из углов параллелограмма на 12°больше другого угла. Найти углы параллелограмма

2. Одна из сторон параллелограмма равна 21, а периметр равен 123. Найти стороны параллелограмма.

3. Одна из сторон параллелограмма на 7 больше другой, а его периметр равен 54. Найти стороны параллелограмма.

4. Диагональ ромба, лежащая против угла в 60°, равна 15. Найти периметр ромба.

5. Периметр ромба на 36 см больше его стороны. Найти сторону ромба.

6. Найти периметр ромба, если его диагонали равны 24 и 32.

7. В прямоугольнике меньшая сторона равна и вдвое меньше диагонали. Найти большую сторону прямоугольника.

8. Найти периметр квадрата, если его диагональ равна .

9. Стороны параллелограмма равны 10 и 15, а одна из диагоналей равна 23. Найти длину второй диагонали.

10.Периметр ромба равен 40, а одна из диагоналей равна 16. Найти длину второй диагонали.

11.Биссектрисы углов A и D параллелограмма пересекаются в точке, лежащей на стороне ВС. Найдите сторону АВ, если ВС = 44см.

12.В выпуклом четырехугольнике два угла прямые, а разность двух других равна 10°. Найти меньший угол.

13.Сколько сторон имеет выпуклый многоугольник, если сумма его внутренних углов равна 4320º.

14.В выпуклом четырехугольнике сумма двух углов равна 110º, а разность двух других равна 20°. Найти больший угол.

15.Две стороны параллелограмма относятся как 3 : 4, а периметр его равен 70. Найдите большую сторону параллелограмма.

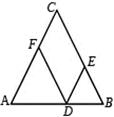
16.Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.

17.

18.Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении
3 : 4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

19.

20.Две стороны параллелограмма относятся как 3 : 4, а периметр его равен 28. Найдите большую сторону параллелограмма.

21.Найдите диагональ прямоугольника, если его периметр равен 28, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 24.

22.Середины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

23.

24.В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на
1 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 28. Найдите меньшую сторону прямоугольника.

25.

26.Найдите высоту параллелограмма ABCD, опущенную на сторону AB, если стороны квадратных клеток равны 1.

27.

Занятие 5

Трапеция. Основные понятия и свойства. Средняя линия трапеции.

Трапеция – четырехугольник, у которого две стороны параллельны, а две другие – нет. Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.

Если боковые стороны равны, трапеция называется равнобедренной. Отрезок, соединяющий середины оснований трапеции, называется средней линией трапеции.

ТЕОРЕМА .Если в трапеции углы при основании равны, то трапеция равнобедренная

ТЕОРЕМА .Если в трапеции диагонали равны, то трапеция равнобедренная

ТЕОРЕМА. Средняя линия трапеции параллельна основаниям и равна их полусумме.

ТЕОРЕМА. В равнобедренной трапеции углы при основании равны, диагонали равны.

ТЕОРЕМА В трапеции отрезок, соединяющий середины диагоналей , равен полуразности оснований

Задания с решениями:

1. Основания трапеции относятся как 2 : 3, а средняя линия равна 5. Найдите меньшее основание.

Решение:

DC : AB=2:3.Тогда DC = 2x, a AB = 3x. Средняя линия EF, . Тогда получим уравнение 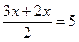, откуда 5х=10, х=2.

Тогда DC = 4, AB = 6. Меньшее основание равно 4.

Ответ: 4

2. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Решение:

EDCB – параллелограмм. Следовательно, по свойствам параллелограмма CB=DE и DC=EB=4. Периметр треугольника равен сумме его сторон, то есть AD+DE+AE =15
Периметр трапеции равен AD+DC+CB+AB=AD+4+EB+AE+4=15+8=23.

Ответ: 23

3. Найдите высоту трапеции АВСD, опущенную из вершины B, если стороны квадратных клеток равны .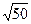

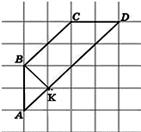
Высота трапеции – это отрезок, перпендикулярный ее основаниям. Проведем отрезок ВК. Из рисунка видно, что ВК перпендикуляр к AD и как диагональ квадратной клетки ВК=

Ответ: 10

4. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Решение:

Построим СМ АМ и СК||DВ. Тогда получим, что BDCK – параллелограмм. Угол ACK прямой, так как он равен углу между диагоналями. Получаем по свойству параллелограмма, что CK = DB, но так как трапеция равнобедренная, то AС=DB=CK, то есть треугольник АСК – равнобедренный, прямоугольный, а значит углы при основании по 45º. Тогда АМ=МК=СМ=12. АК=24. Но АК=АВ+ВК=АВ+DC. Средняя линия равна

Ответ: 12

5. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.

Решение:

Пусть СЕ – высота и АЕ = 10, а ЕВ = 4. Проведем вторую высоту:
DK АВ. Так как трапеция равнобедренная, то треугольники ADK и CBE равны по гипотенузе и катету. Тогда АК = 4, КЕ = 10 – 4 = 6. DCEK – прямоугольник, и значит DC = KE = 6. АВ = 10 + 4 = 14. Средняя линия равна .

Ответ: 10