Задания для самостоятельного решения. 1. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?

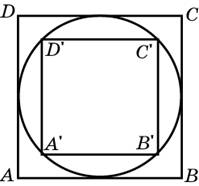
1. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?

2. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен .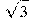

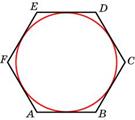
3. Сторона правильного треугольника равна 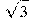. Найдите радиус окружности, вписанной в этот треугольник.

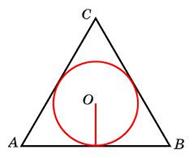
4. Радиус окружности, вписанной в правильный треугольник, равен 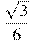. Найдите сторону этого треугольника.

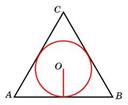
5. Найдите радиус окружности, вписанной в квадрат со стороной 4.

6. Найдите сторону квадрата, описанного около окружности радиуса 4.

7. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .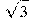

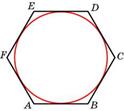
8. Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.

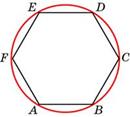
9. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 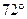. Найдите n.

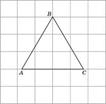
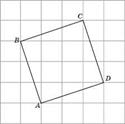
10. Найдите радиус окружности, описанной около правильного треугольника ABC, считая стороны квадратных клеток равными 1.

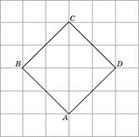
11. Найдите радиус окружности, вписанной в четырехугольник ABCD. В ответе укажите .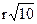

12. Около окружности, радиус которой равен 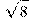, описан квадрат. Найдите радиус окружности, описанной около этого квадрата.

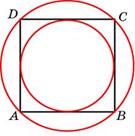
13. Около окружности, радиус которой равен 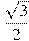, описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.

14. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .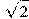

15. В окружность вписаны правильный треугольник и правильный шестиугольник. Найти площадь треугольника, если периметр шестиугольника равен 36.

16. В окружность вписаны квадрат и правильный шестиугольник. Найти площадь квадрата, если периметр шестиугольника равен 24.

17. В окружность вписаны правильный треугольник и квадрат. Найти площадь квадрата , если площадь треугольника равна 9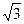

18. В круг вписан правильный треугольник. Найти площадь треугольника и площадь круга, если длина окружности данного круга равна 20 .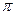

19. В квадрат, площадь которого равна 16 вписан круг. Найти его площадь и длину окружности

20. В круг, площадь которого равна 100 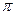, вписан правильный шестиугольник. Найти его площадь..

21. В правильный треугольник, периметр которого равен 6, вписан круг. Найти его площадь и длину окружности

22. В круг, у которого длина окружности равна 10 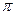, вписан правильный шестиугольник. Найти его площадь.

23. Найти площадь круга, описанного около правильного треугольника со стороной 8.

24. Найти радиус круга, описанного около правильного треугольника, высота которого равна 18.

25. Медиана правильного треугольника равна 24.Найти площадь круга, вписанного в этот треугольник.

26. Меньшая диагональ правильного шестиугольника равна 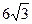.Найти длину окружности, описанной около этого шестиугольника.

27. Сторона правильного шестиугольника равна 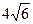.Найти сторону правильного треугольника, равновеликого данному шестиугольнику.

28. Радиус окружности, описанной около правильного шестиугольника равна12.Найти длину меньшей диагонали шестиугольника

29. Точка О является центром правильного девятиугольника ABCDEFGHK. Площадь треугольника OAD равна 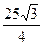. Найти длину перпендикуляра ОМ, опущенного на диагональ AD.

30. В круге радиусом 12 проведены по одну сторону от центра две параллельные хорды, из которых одна стягивает дугу в 120º, а другая в 60º. Найти площадь части круга, заключенную между хордами.

31. Из точки, лежащей на окружности проведены две хорды, длина каждой из которых равна радиусу. Найти угол между этими хордами.

32. Площадь квадрата, описанного около окружности , равна 16.Найти площадь правильного треугольника, вписанного в ту же окружность.

33. Сумма площадей правильного четырехугольника, описанного около окружности и правильного треугольника , вписанного в эту окружность, равна 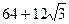Найти длину окружности

34. Сторона правильного восьмиугольника ABCDEFGH равна 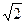. Найти радиус окружности, вписанной в четырёхугольник MNPK, если точки M, N, P, K - середины сторон AB, CD, EF и GH соответственно