Метод исследования рассуждений посредством таблично построенной логики высказываний.

Логикавысказываний, построеннаятабличным способом, даетэффективнуюпроцедурудлявыявления законовлогики, атакжеметодпроверкиправильности рассуждении. Рассуждениесчитаетсяправильным, если междуегопосылкамиизаключениемимеетместо отношениелогическогоследования. Определяемпоследнее:

из посылокГследует заключениеВ, если импликация, имеющая антецедентом конъюнкцию формул, соответствующих посылкам, а консеквентом — формулу, соответствующую заключению, является тождественноистинной.

Пустьданорассуждение: “ЕслиИвановявляется участникомэтогопреступления, тоонзналпотерпевшего.

Ивановнезналпотерпевшего, нозналегожену. ПотерпевшийзналИванова. Следовательно, Иванов являетсяучастникомэтогопреступления”. Дляопределения правильностирассуждениятребуется: во-первых, обозначитьразличнымисимволами

различныепростыевысказывания, входящиеврассуждение. Вприведенномрассуждениивстречаютсяследующие простыевысказывания: “Ивановявляетсяучастникомэтого преступления”, “Ивановзналпотерпевшего”, “Ивановзнал женупотерпевшего”. “ПотерпевшийзналИванова”.

Обозначимихсоответственносимволамиp,q, r, s; во-вторых, перевестинаязыклогикивысказываний

посылкиизаключение. Переводомпосылокявляются формулырÉq,Øq Ù r, s, апереводомзаключения — формулар (союз “но” соответствуетвданномслучаесоюзу

“и”); в-третьих, формулы, являющиесяпереводомпосылок,

последовательносоединитьзнакомконъюнкции. Получаем формулу:

((p Éq)Ù (ØqÙr )) Ùs;

в-четвертых, кполученнойформулеприсоединить

справазнакомимпликацииформулу, являющуюся переводомзаключения. Получаемформулу:

((рÉq)Ù (ØqÙr))ÙsÉр;

в-пятых, дляполученнойформулыпостроитьтаблицу

истинности.

Еслиформула, являющаясяпереводомрассужденияна языксимволов, оказываетсятождественно-истинной, то можносделатьвыводотом, чторассуждениеправильное, еслитождественно-ложной, торассуждениенеправильное. Можетоказаться, чтоформулаявляетсявыполнимой, ноне тождественно-истинной. Втомслучаенетоснований считать рассуждение правильным. Необходимопродолжить анализрассуждения, ноужесредствамиболеебогатого разделалогики — средствамилогики предикатов.

Вернемсякрассматриваемомурассуждению. Построим таблицуистинностидляформулы, являющейсяпереводом этогорассуждениянаязыксимволов: ((рÉq)Ù (ØqÙ r))ÙsÉр и и и л л и л и л и и и и и и л л и л и л л и и и и и л л и л л л и и и и и и л л и л л л л и и и л л л и л и и л и и и и л л л и л и и л л и и и л л л и л л л л и и и и л л л и л л л л л и и л и и л л и л и л и и л л и и л л и л и л л и л л и и л л и л л л и и л л и и л л и л л л л и л л и л и и л и и и и л л л и л и и л и и л л и л л и л л и л л л л и и л л и л л и л л л л л и л .

Формулаявляетсявыполнимой, нонеобщезначимой. Следовательно, нетоснованийсчитатьрассматриваемое рассуждениеправильным.

Еслиформуласодержитмногопеременных, тов некоторыхслучаяхможнонестроитьтаблицу, апутем особых “сокращающих” рассужденийустановить,является лионаобщезначимой, противоречивойилижевыполнимой, нонеобщезначимой.

Рассмотримпроанализированнуювышеформулу. Предположим, чтопринекоторомнаборезначений переменныхонапринимаетзначение “л”:

((p Éq)Ù(Øq Ù r))Ùs Ép

Этовозможно, еслизначениеконсеквента — “л”, а антецедента — “и”,аследовательно, каждогочлена конъюнкции — “и”:

((p Éq)Ù(Øq Ù r))Ùs Ép и и и л л

Посколькупеременнойружеприписанозначение “л”, пишем “л” подпервымвхождениемрвформулу:

((p Éq)Ù(Øq Ù r))Ùs Ép л и и и л л

ПодформулаØqÙ rимеетзначение “и”, если, итолько если, Øqиrимеютзначение “и”:

((p Éq)Ù(Øq Ù r))Ùs Ép л и и и и и л л

ПосколькуподформулаØqимеетзначение “и”, подq пишем “л”:

((p Éq)Ù(Øq Ù r))Ùs Ép л и и л и и и л л

Тогда

((p Éq)Ù(Øq Ù r))Ùs Ép л и л и и л и и и и л л

Формулапринимаетзначения “л” призначениях “л”, “л”, “и”, “и” соответственнопеременныхр, q, r и s.

Очевидно, чтопризначении “и” переменнойэта формулапринимаетзначение “и”. Формулапринимаеткак значение “л”, такизначение “и”, аследовательно, является выполнимой, нонеобщезначимой.

Рассмотримформулу:

((p Éq)Ù(q É r))Ùp Ér

Чтобыдоказать, чтоформулаявляетсяобщезначимой, будемрассуждатьотпротивного. Предположим, чтоонане общезначима, т.е. принекоторомнаборезначений переменныхпринимаетзначение “л”. Этовозможно, еслиее антецедент, аследовательно, каждыйчленконъюнкции принимаетзначение “и”:

((p Éq)Ù(q É r))Ùp Ér и и и и и л л

((p Éq)Ù(q É r))Ùp Ér и и и и л и л и и л л

Приходимкпротиворечию, таккаквэтомслучае, чтобыантецедентимпликацииоставалсяистинным, первомувхождению переменнойqследуетприписать значение “и”, авторому — “л”. Следовательно, формула являетсяобщезначимой.

Ещеодинспособустановленияотношениялогического следованиямеждусуждениями, атакжеидругих отношений, заключаетсявследующем: сужденияпереводятсянаязыклогикивысказываний; дляформул, соответствующихсуждениям, строятся

сравнимыетаблицыистинности; устанавливаютсявидыотношениймеждусуждениями

наосновеследующихопределений:

1) суждениясовместимыпоистинности, еслиитолько есливсравнимыхтаблицахестьстрока, вкоторойвсе формулыимеютзначение “истина”;

2) суждениясовместимыположности, еслиитолько есливсравнимыхтаблицахестьстрока, вкоторойвсе формулыимеютзначение “ложь”;

3) изсужденийА₁, А₂ , ..., A_nследуетсуждениеВ,еслии толькоесливсравнимыхтаблицахнетстроки, вкоторойвсе формулы, соответствующиесуждениямА₁, А₂ , ..., A_n, имеют значение “истина”, аформула, соответствующаясуждению В, имеетзначение “ложь”.

Остальныеотношенияявляютсяпроизводнымипоотношениюкназванным.

Пример: Пустьпереводамитрехсужденийявляются, соответственно, формулыØr Ùр, p É q Úr, q.Построим дляэтихформултаблицыистинноститакимобразом, чтобы этитаблицыможнобылосравнивать. Дляэтоговыпишем вначалевсепеременные, входящиевкакие-либоизэтих формул. Этопеременныер, q, r . Числостроктаблиц = 2³ = 8. Строимтаблицы:

Междупервымидвумясуждениямиипоследнимимеет местоотношениелогическогоследования. Этисуждения (всетри) совместимыпоистинности (см. строку 5) ине совместимыположности.

15.Фигуры силлогизмов.

Фигураминазываютсятипысиллогизмов, выделяемые наосновеспособоврасположениятерминоввпосылках:

I фигура II фигура III фигура IV фигура

Сначаланужновыделитьменьшийибольшийтерминыв заключении. Меньшийтермин(s), большийтермин(F). Посылка, вкоторуювходитменьшийтермин, называется меньшей. Посылка, вкоторуювходитбольшийтермин, называетсябольшей. Имеетсясреднийтермин. Правилатрехпервыхфигур.

Правила I фигуры:

1) большаяпосылкадолжнабытьобщимсуждением

(единичноесуждениеобычноотождествляетсясобщим);

2) меньшаяпосылкадолжнабытьутвердительным суждением.

Правила II фигуры:

1) большаяпосылкадолжнабытьобщимсуждением;

2) однаизпосылокдолжнабытьотрицательным суждением

Правила III фигуры: 1) меньшаяпосылкадолжнабытьутвердительным суждением;

2) заключениедолжнобытьчастнымсуждением.

Приисследованиисиллогизмовтакжеможно использоватькруговыесхемы. Графическийметод заключаетсявследующем. Выявляютсяипредставляются посредствомкруговыхсхемвсевозможныеотношения междутерминамиоднойпосылки, затем — второй, при которыхпосылкиистинны. Послеэтогосоответствующие схемысовмещаются ипроверяется, истиннолизаключение прикаждомсовмещениивыделенныхсхем. Еслида, то силлогизмправильный.

Дляустановлениянеправильностисиллогизма достаточнообнаружитьхотябыодноотношениемежду терминамисиллогизма, прикоторомпосылкиистинны, а заключениеложно.

Рассмотримсиллогизм:

Вседельфины — киты.

____Ниоднарыбанеявляетсякитом.

Ниоднарыбанеявляетсядельфином.

Егоструктура:

ВсеР сутъМ.

НиодинSнесутьМ.

НиодинSнесутьР.

Возможныеотношениямеждутерминамибольшей посылки, прикоторыхонаистинна:

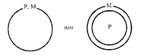
Меньшаяпосылкаистинналишьприодномотношении междуеетерминами:

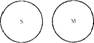
Возможныследующиесовмещениясхем:

P.M. S

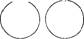
М S

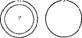
Силлогизмправильный.

Ещепример:

Всемарксисты — диалектики. Всеавторыэтойкниги — диалектики. Следовательно, всеавторыэтойкниги — марксисты.

ВсеРсутьМ.

Структура:ВсеSсутьМ.

ВсеSсуть Р.

Круговаясхема:

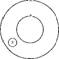
Умозаключениенеправильное.

Силлогизмыневсегдавысказываютсяполностью. Частооднаизпосылокилизаключениеопускаются. Такие рассужденияназываютсяэнтимемами.

Дляпроверкиправильностиэнтимемынужно попытатьсявосстановитьпропущеннуючастьтаким образом, чтобыполучилсяправильныйсиллогизм. Если этогосделатьнельзя, тоэнтимемаявляетсянеправильной, еслиудается, топравильной.

Приисследованииэнтимемывпроцессеаргументации целесообразнопопытатьсяустановить, являетсяли восстановленнаяпосылкасиллогизмаистиннойили ложной. Еслионаоказываетсяистинной, тоаргументация корректная, впротивномслучае — некорректная.