Явление состязания элементов памяти рассматривалось в работе асинхронного автомата. Устранение данного явления в синхронном автомате можно сделать следующими двумя способами:
1. за счет выбора минимально необходимой длительности сигнала синхронизации;
2. использованием структуры автомата с двойной памятью.
Первый способ был рассмотрен ранее в примере структурного этапа канонического метода синтеза синхронного автомата, но обычно на практике этот способ не используется, так как сложно построить генератор сигнала синхронизации с такими жесткими требованиями к его длительности.
Обычно используется структура автомата с двойной памятью. Структурная схема такого автомата представлена на рис. 6.54. Блок памяти состоит из двух ступеней памяти, каждая из которых тактируется своим сигналом синхронизации: первая (входная) – сигналом C1, вторая (выходная) - сигналом C2.
Входная ступень блока памяти служит для запоминания нового состояния автомата, в то время, когда выходная ступень; определяющая состояние автомата, сохраняет код старого состояния.
Рис. 6.54
На рис. 6.55 приведена временная диаграмма работы автомата с двойной памятью:
Рис. 6.55
К начальному моменту времени t0 обе ступени блока памяти должны быть установлены в начальное состояние и на входы автомата поданы нужное значения входных сигналов xi.
В интервале времени t0 – t1 в комбинационной схеме автомата происходит формирование значений функций возбуждения и выхода автомата.
К моменту t1 эти значения должны быть сформированы и по фронту сигнала синхронизации С1 = 1 в течение интервала t1 – t2 происходит запись нового значения кода состояния в первую (входную) ступень блока памяти, при этом в это время может возникнуть состязание элементов памяти первой ступени, но это состязание не будет влиять на работу автомата, так как запись во вторую ступень запрещена, потому что C2 = 0 и на выходах блока памяти сохраняется код старого состояния. Таким образом, состязание элементов памяти первой ступени является не критическим. Длительность сигнала С1 должна быть достаточна для записи кода нового состояния во все триггеры первой ступени.
К моменту t3 состязание элементов памяти первой ступени должны быть закончены и на входах второй ступени блока памяти должны быть установлены значения кода нового состояния. По фронту сигнала синхронизации С2 = 1 в течение интервала t3 – t4 происходит перезапись значения кода нового состояния из первой (входной) ступени во вторую (выходную) ступень блока памяти. При этом могут возникнуть состязание элементов памяти второй ступени, но это состязание не будет влиять на работу автомата, так как запись возникших неправильных значений функций возбуждения в первую (входную) ступень запрещена, потому что C1 = 0. Таким образом, состязание элементов памяти второй ступени блока памяти, также будет не критическим. Длительность сигнала С2 должна быть достаточна для записи кода нового состояния во все триггеры второй ступени блока памяти.
В интервале t3 – t4, при С2 = 1 меняется значения на выходах элементов блока памяти yj, которые поступают на входы комбинационной схемы и следовательно, целесообразно в это же время менять и входные сигналы xi.
В интервал t4 – t5 в комбинационной схеме автомата формируются функции выхода и функции возбуждения. Длительность этого интервала выбирается минимально необходимой для формирования функции возбуждения и функции выхода и определяется глубиной комбинационной схемы.
К моменту времени t5 при С1 = 1 значения на выходах комбинационной схемы уже стабильны, и при С1 = 1 можно считывать значения функций выхода zj.
Структурная схема автомата с двойной памятью и двумя сериями сигналов синхронизации используется в управляющих устройствах, которые эксплуатируются в неблагоприятных условиях при больших колебаниях температуры внешней среды.
В нормальных условиях обычно вместо двух серий сигналов синхронизации используют прямое и инверсное значение одного сигнала синхронизации. При С = 1 срабатывает первая (входная) ступень, а при С = 0 вторая (выходная) ступень блока памяти.
При синхронизации двойной памяти одной серией сигналов синхронизации, в качестве элементов памяти используются синхронные триггеры с логической задержкой, т.е. двухступенчатые триггеры, построенные по схеме Master-Slave.
Пример реализации синхронного автомата структурой с двойной памятью и одной серией сигнала синхронизации:
Пусть задан граф автомата Мили рассмотренный ранее в каноническом методе синтеза и реализованный ранее структурой с одной ступенью памяти (рис. 6.56).
Рис. 6.56
Таблица 6.19
| x y1y2 | | |
| 0 1 | 11 /0 | 11 /0 |
| 1 1 | 10 /0 | 10 /0 |
| 1 0 | 01 /1 | 01 /0 |
После произвольного кодирования трех состояний автомата следующим образом: s0 = 01, s1 = 11, s2 = 10, была получена кодированная таблица переходов и выходов (табл. 6.19) и по этой таблице была построена следующая система булевых функций возбуждения элементов памяти и выхода автомата:
z =  2;
2;
y’S1 =  1, y’R1 =
1, y’R1 =  2;
2;
y’S2 =  2, y’R2 = y1 y2.
2, y’R2 = y1 y2.
Структурная схема синтезируемого автомата с двойной памятью представлена на рис. 6.54, только в качестве элемента памяти используется RS-триггер. Комбинационная схема реализует систему следующих пяти булевых функций: z – функция выхода, y’S1, y’R1 - функции возбуждения триггера первой ступени T11, y’S2, y’R2 - функции возбуждения триггера первой ступени T12, зависящих от трех переменных: х, у1, у2.
 1 q1 1 q1 |
 2 2 |
 1 1 |
 2 2 |
 2 2 |
 1 1 |
 2 2 |
 2 2 |
Рис. 6.57
К выходам логических схем, реализующих функции возбуждения, подключаются элементы памяти, образующие двойную память автомата.
В результате получается следующая функциональная схема автомата с двойной памятью (рис. 6.57). Для проверки правильности ее построения необходимо протестировать его работу на конкретном входном слове. На рис. 6.58 представлена временная диаграмма работа автомата по переработке входного слова 1 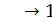 0. Это слово перерабатывается в выходное слово 0
0. Это слово перерабатывается в выходное слово 0  0
0  1.
1.
По сигналу P = 1 к моменту времени t0 обе ступени блока памяти должны быть установлены в начальное состояние s0 = 01 и на входы автомата поданы нужное значения входного сигнала x.
В интервале времени t0 – t1 в комбинационной схеме автомата происходит формирование значений функций возбуждения и выхода автомата.
К моменту t1 эти значения должны быть сформированы и по фронту сигнала синхронизации С = 1 в течение интервала t1 – t2 происходит запись нового значения кода состояния в первую (входную) ступень блока памяти, при этом в это время может возникнуть состязание элементов памяти первой ступени, но это состязание не будет влиять на работу автомата, так как запись во вторую ступень запрещена, потому что C = 0 и на выходах блока памяти сохраняется код старого состояния. Таким образом, состязание элементов памяти первой ступени является не критическим. Длительность сигнала С = 1 должна быть достаточна для записи кода нового состояния во все триггеры первой ступени.
К моменту t2 состязание элементов памяти первой ступени должны быть закончены и на входах второй ступени блока памяти должны быть установлены значения кода нового состояния. По спаду сигнала синхронизации С = 1 в течение интервала t2 – t3 происходит перезапись значения кода нового состояния из первой (входной) ступени во вторую (выходную) ступень блока памяти. При этом могут возникнуть состязание элементов памяти второй ступени, но это состязание не будет влиять на работу автомата, так как запись возникших неправильных значений функций возбуждения в первую (входную) ступень запрещена, потому что C = 0. Таким образом, состязание элементов памяти второй ступени блока памяти, также будет не критическим. Длительность сигнала С должна быть достаточна для записи кода нового состояния во все триггеры второй ступени блока памяти.
В интервале t2 – t3, при С = 0 меняется значения на выходах элементов блока памяти y1 и y2, которые поступают на входы комбинационной схемы и следовательно, целесообразно в это же время менять и входной сигнал x. Далее в этом же интервале t2 – t3 в комбинационной схеме автомата формируются значения функции выхода и функции возбуждения. Длительность этого интервала выбирается минимально необходимой для формирования функции возбуждения и функции выхода, после изменения значений входных сигналов, и определяется глубиной комбинационной схемы.
К моменту времени t3 при С = 1 значения на выходах комбинационной схемы уже стабильны, и по фронту С = 1 можно считывать значения функции выхода z и значения функции возбуждения элементов памяти. Далее этот процесс повторяется до переработки всего входного слова и возврата автомата в начальное состояние.
Расчет параметров сигнала синхронизации
Длительность сигнала синхронизации выбирается следующим образом: вначале определяются логические элементы, которые меняют свое состояние при этом значении синхросигнала и определяется их число в самой длиной цепочке из этих элементов. Длительность определяется из условия, что все элементы, которые должны изменить свое состояние успели это сделать.
Тогда t1 - длительность сигнала синхронизации С = 1 определяется временем срабатывания триггеров первой ступени t1 = ∆τ + 2 ∆τ = 3 ∆τ, где 2 ∆τ время срабатывания базового RS-триггера. Длительность t0 - сигнала синхронизации С = 0 определяется суммой времён срабатывания триггеров второй ступени: 2 ∆τ + 2 ∆τ = 4 ∆τ и времени формирования в комбинационной схеме значений функций - ∆τ, так как длина цепочки в комбинационной схеме равна единице, итого: t0 = 4 ∆τ + ∆τ = 5 ∆τ.
T = t1 + t0 = 3 ∆τ +5 ∆τ = 8 ∆τ
Рис. 6.58
6.6. Построение комбинационной схемы асинхронного автомата
Существенным отличием структурного синтеза асинхронного автомата от синтеза синхронного автомата является необходимость построениякомбинационной схемы без, так называемого, “явления риска”. Причина этого явления состоит в том, что реальные логические элементы обладают определенной задержкой во времени срабатывания, причем величина задержки заранее не известна и зависит от технологии изготовления и от внешних факторов в процессе эксплуатации, поэтому определить соотношение задержек различных логических элементов заранее не возможно.
Для анализа этого явления используется следующая модель реального логического элемента, которая состоит из идеального логического элемента (ИЛЭ) и элемента задержки ∆τ (рис.6.59). Задержкой обладают также линии связи, но эти задержки относят к задержкам логических элементов.
Рис.6.59
Величина задержки ∆τ зависит от температуры, от расположения в схеме, нагрузки, влажности и других факторов. Величина задержки по техническому паспорту может меняться в следующих пределах:
∆τ min < ∆τ < ∆τ max
Из-за разброса значений ∆τ разных логических элементов в схеме из этих элементов возникает так называемое явление риска (далее просто риск). Риск возникают при смене одного набора значений входных переменных на другой набор значений и проявляется в появлении на выходе схемы кратковременного неправильного значения реализуемой функции.
На рис. 6.60 приведена логическая схема, реализующая функцию трех переменных: f (x1x2x3) =  1 x3 V x2
1 x3 V x2  3 :
3 :
 1 1 |
 3 3 |
Рис. 6.60
Пусть существует два набора значений входных переменных x1x2x3: σ1 = 010 и σ2 = 011, таких что f (σ1 ) = f (σ2 ) =1. Пусть задержка первого элемента ∆1 больше задержки второго элемента ∆2 т.е. ∆1 > ∆2 и пусть для простоты ∆3 = 0.
Временная диаграмма работы схемы при смене набора σ1 на набор σ2 приведена на рис. 6.61.
Рис. 6.61
На рис. 6.61 видно, что на выходе схемы ненадолго появляется 0 - это называется явлением риска.
Статический риск.
Определение: пусть существует функция f(  ) и существуют два набора значений входных переменных σ1 и σ2, таких что f (σ1 ) = f (σ2 ), тогда если при смене набора σ 1 на σ 2 на выходе схемы появляется значение, отличное от f (δ1 ) , то говорят что в схеме имеет место статический риск.
) и существуют два набора значений входных переменных σ1 и σ2, таких что f (σ1 ) = f (σ2 ), тогда если при смене набора σ 1 на σ 2 на выходе схемы появляется значение, отличное от f (δ1 ) , то говорят что в схеме имеет место статический риск.
Статические риски бывают:
a) статический риск в «1» (рис. 6.62).
Рис. 6.62
b) статический риск в «0» (рис. 6.63).
Рис. 6.63
Следует отметить, что если ∆1 < ∆2, то статический риск в «1» в схеме (рис. 6.61) отсутствует.
Динамический риск.
Определение: пусть существует функция f(  ) и существуют два набора значений входных переменных σ1 и σ2, таких что f (σ1 ) ≠ f (σ2 ), тогда если при смене набора σ 1 на σ 2 на выходе схемы появляется следующая последовательность значений: f (σ1 ) →f (σ2 ) →f (σ1 ) →f (σ2 ) , то говорят, что в схеме имеет место динамический риск.
) и существуют два набора значений входных переменных σ1 и σ2, таких что f (σ1 ) ≠ f (σ2 ), тогда если при смене набора σ 1 на σ 2 на выходе схемы появляется следующая последовательность значений: f (σ1 ) →f (σ2 ) →f (σ1 ) →f (σ2 ) , то говорят, что в схеме имеет место динамический риск.
На рис. 6.64 приведена логическая схема, реализующая функцию пяти переменных: f (  ) = (
) = (  1x2 v x1x3 ) (
1x2 v x1x3 ) (  1x4 v x5 ):
1x4 v x5 ):
 1 1 |
 1 1 |
Рис. 6.64
Пусть существует два набора значений переменных x1x2x3x4x5:
σ1 = 01110 и σ2 = 11110, таких что f (σ1 ) = 1, f (σ2 ) =0. Пусть между задержками первых трех элементов существует следующие соотношения: ∆1 < ∆2 < ∆3 и пусть для простоты ∆4 = ∆5 = ∆6 = 0.
Временная диаграмма работы схемы при смене набора σ1 на набор σ2 приведена на рис. 6.65.
Рис. 6.65
Из временной диаграммы видно, что при таком соотношении между задержками логических элементов, в схеме имеет место динамический риск.
Существует динамический риск при переключении 0 → 1 и динамический риск 1 → 0 (рис. 6.66).
Рис. 6.66
Наличие риска в комбинационной схеме автомата приводит к его неправильной работе.
В синхронном автомате явление риска исключается за счет выбора периода и длительности сигнала синхронизации. Длительность синхросигнала должен быть больше времени срабатывания самой длинной цепочки элементов в схеме. За это время все процессы по формированию значений функций должны быть завершены.
Для построения асинхронного автомата необходимо использовать комбинационные схемы без риска.
Построение схем без риска.
В рассматриваемом способе исключения явления риска на комбинационные схемы накладывают следующие ограничения:
1. при смене набора значений входных переменных не может одновременно меняться значение более чем одной переменной;
2. глубина комбинационной схемы не должна быть более двух, т.е. схема должна иметь не более двух ярусов.
Наличие этих двух ограничений означает, что использование этого способа позволяет устранить только статический риск.
В двухъярусной схеме возможно два варианта схем:
1. cхема построенная по дизъюнктивной нормальной форме (ДНФ).
f ДНФ = k1 ˅ k2 ˅ … ˅ km, где: ki – конъюнкция (рис. 6.67);
2. схема построенная по конъюнктивной нормальной форме (КНФ).
f KНФ = d1 ˄ d2 ˄ … ˄ dn, где: di – дизъюнкция (рис. 6.68).
Рис. 6.67
Рис. 6.68
Из анализа этих схем можно сделать следующие утверждения:
1. в двухъярусной схеме, построенной по ДНФ, статический риск в «0» отсутствует.
2. в двухъярусной схеме, построенной по КНФ статический риск в «1» отсутствует.
3. пусть есть схема, построенная по ДНФ и пусть переменная xi входит в эту ДНФ только в прямом или только инверсном виде, тогда при изменении значения этой переменной статический риск в схеме отсутствует.
4. если есть схема, построенная по КНФ и если переменная xi входит в эту КНФ только в прямом или только инверсном виде, тогда при изменении значения этой переменной статический риск в схеме отсутствует.
5. если есть схема, построенная по ДНФ, и если переменная xi входит в эту ДНФ, как в прямом, так и в инверсном виде, тогда в схеме может возникнуть статический риск в «1» при изменении значения этой переменной.
Для доказательства исходная ДНФ представляется в виде:
fДНФ = A ˅ B(xi) ˅ C(  i), где: A – группа конъюнкций не содержащих xi; B(xi) - группа конъюнкций содержащих xi в прямом виде; C(
i), где: A – группа конъюнкций не содержащих xi; B(xi) - группа конъюнкций содержащих xi в прямом виде; C(  i) - группа конъюнкций содержащих xi в инверсном виде (рис. 6.69).
i) - группа конъюнкций содержащих xi в инверсном виде (рис. 6.69).
 i i |
Рис. 6.69
Пусть σ1 и σ2 два набора значений переменных отличающихся значением только по переменной xi, причем f(σ1) = f(σ2) = 1.
Возможны различные ситуации:
I. Если A(σ1) = A(σ2) = 1, то в этом случае риска нет, так как единица на выходе группы A обеспечит значение единица на выходе всей схемы;
II. A(σ1) = A(σ2) = 0, то в этом случае значение единица на выходе всей схемы обеспечивается конъюнкциями группы B или конъюнкциями группы C, т.е. возможны два варианта:
1. B(σ1) = 1 C(σ1) = 0;
B(σ2) = 0, C(σ2) = 1.
При этом возможны следующие три ситуации:
a. ∆B = ∆C - риска нет, но это нереальная ситуация;
b. ∆B < ∆C – риск есть (рис. 6.70);
Рис. 6.70
c. ∆B > ∆C - риска нет (рис. 6.71)
Рис. 6.71
2. B(σ1) = 0 C(σ1) = 1;
B(σ2) = 1, C(σ2) = 0.
При этом возможны следующие три ситуации:
a. ∆B = ∆C - риска нет, но это нереальная ситуация;
b. ∆B < ∆C – риска нет (рис. 6.72);
Рис. 6.72
c. ∆B > ∆C - риск есть (рис. 6.73).
Рис. 6.73
6. если есть схема, построенная по КНФ, и если переменная xi входит в эту КНФ, как в прямом, так и в инверсном виде, тогда в схеме может возникнуть статический риск в «0» при изменении значения этой переменной.
Для доказательства исходная КНФ представляется в виде:
f КНФ = A ˄ B(xi) ˄ C(  i), где: A – группа дизъюнкций не содержащих xi; B(xi) - группа дизъюнкций содержащих xi в прямом виде; C(
i), где: A – группа дизъюнкций не содержащих xi; B(xi) - группа дизъюнкций содержащих xi в прямом виде; C(  i) - группа дизъюнкций содержащих xi в инверсном виде (рис. 6.74).
i) - группа дизъюнкций содержащих xi в инверсном виде (рис. 6.74).
 i i |
Рис. 6.74
Пусть σ1 и σ2 два набора значений переменных отличающихся значением только по переменной xi, причем f(σ1) = f(σ2) = 0.
Возможны различные ситуации:
I. A(σ1) = A(σ2) = 0 – то в этом случае риска нет, так как ноль на выходе группы A обеспечит значение ноль на выходе всей схемы;
II. A(σ1) = A(σ2) = 1 – то в этом случае значение ноль на выходе всей схемы обеспечивается дизъюнкциями группы B или дизъюнкциями группы C, т.е. возможны два варианта:
1. B(σi) = 0 C(σi) = 1;
B(σi) = 1 C(σi) = 0.
При этом возможны следующие три ситуации:
a. ∆B = ∆C - риска нет, но это нереальная ситуация;
b. ∆B < ∆C – риск есть (рис. 6.75);
Рис. 6.75
c. ∆B > ∆C - риска нет (рис. 6.76).
Рис. 6.76
2. B(σi) = 1 C(σi) = 0;
B(σi) = 0 C(σi) = 1.
a. ∆B = ∆C - риска нет, но это нереальная ситуация;
b. ∆B < ∆C – риска нет (рис. 6.77);
Рис. 6.77
c. ∆B > ∆C - риск есть (рис. 6.78).
Рис. 6.78
Из рассмотрения приведенных утверждений видно, что в некоторых случаях риск, который может возникнуть из за наличия разных значений на выходах элементов группы B и C, “шунтируется” наличием нужного значения на выходах элементов группы A. Поэтому идея построения схемы без риска заключается в выявлении наборов значений переменных σ1 и σ2, при смене которых может возникнуть риск, и добавлении к схеме элемента группы A, который обеспечит отсутствие риска в схеме для этой конкретной пары наборов σ1 и σ2.
Алгоритм построения схемы без риска по ДНФ.
Пусть задана в ДНФ функция f(x1x2…xn) от n переменных.
1. задается i := 1 - индекс переменной xi;
2. относительно текущей переменной xi исходная ДНФ представляется в виде: fДНФ = A v B (xi) v C  i) ;
i) ;
3. для xi определяются пары наборов σ1 и σ2, соседних по переменной xi и для которых f(σ1) = f(σ2) = 1;
4. для каждой такой пары σ1 и σ2 определяются значения конъюнкций группы A;
Если A(σ1) = A(σ2) = 0, то риск возможен, и для выявленной пары σ1 и σ2 образуется конъюнкция, которая сохраняет значение 1 на обоих наборах σ1 и σ2 и не содержит xi. Полученная конъюнкция добавляется к ДНФ, а в схему включается конъюнктор реализующий эту конъюнкцию;
5. индекс переменной увеличивается i:= i + 1 и, если i ≤ n, то переход к п.2, иначе конец работы алгоритма.
Пример построения схемы без риска по ДНФ:
Пусть fДНФ(x1x2x3) =  1
1  3 v x2x3.
3 v x2x3.
Риск возможен по переменной x3, так как только она входит в ДНФ как в прямом, так и в
 2;
2; 1, y’R1 =
1, y’R1 =  2;
2; 2, y’R2 = y1 y2.
2, y’R2 = y1 y2. 1 q1
1 q1  2
2  1
1  2
2  2
2  1
1  2
2  2
2 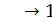 0. Это слово перерабатывается в выходное слово 0
0. Это слово перерабатывается в выходное слово 0  0
0  1.
1. 1 x3 V x2
1 x3 V x2  3 :
3 : 1
1  3
3  ) и существуют два набора значений входных переменных σ1 и σ2, таких что f (σ1 ) = f (σ2 ), тогда если при смене набора σ 1 на σ 2 на выходе схемы появляется значение, отличное от f (δ1 ) , то говорят что в схеме имеет место статический риск.
) и существуют два набора значений входных переменных σ1 и σ2, таких что f (σ1 ) = f (σ2 ), тогда если при смене набора σ 1 на σ 2 на выходе схемы появляется значение, отличное от f (δ1 ) , то говорят что в схеме имеет место статический риск. ) и существуют два набора значений входных переменных σ1 и σ2, таких что f (σ1 ) ≠ f (σ2 ), тогда если при смене набора σ 1 на σ 2 на выходе схемы появляется следующая последовательность значений: f (σ1 ) →f (σ2 ) →f (σ1 ) →f (σ2 ) , то говорят, что в схеме имеет место динамический риск.
) и существуют два набора значений входных переменных σ1 и σ2, таких что f (σ1 ) ≠ f (σ2 ), тогда если при смене набора σ 1 на σ 2 на выходе схемы появляется следующая последовательность значений: f (σ1 ) →f (σ2 ) →f (σ1 ) →f (σ2 ) , то говорят, что в схеме имеет место динамический риск. ) = (
) = (  1x2 v x1x3 ) (
1x2 v x1x3 ) (  1x4 v x5 ):
1x4 v x5 ): 1
1  1
1  i), где: A – группа конъюнкций не содержащих xi; B(xi) - группа конъюнкций содержащих xi в прямом виде; C(
i), где: A – группа конъюнкций не содержащих xi; B(xi) - группа конъюнкций содержащих xi в прямом виде; C(  i) - группа конъюнкций содержащих xi в инверсном виде (рис. 6.69).
i) - группа конъюнкций содержащих xi в инверсном виде (рис. 6.69). i
i  i), где: A – группа дизъюнкций не содержащих xi; B(xi) - группа дизъюнкций содержащих xi в прямом виде; C(
i), где: A – группа дизъюнкций не содержащих xi; B(xi) - группа дизъюнкций содержащих xi в прямом виде; C(  i) - группа дизъюнкций содержащих xi в инверсном виде (рис. 6.74).
i) - группа дизъюнкций содержащих xi в инверсном виде (рис. 6.74). i
i  i) ;
i) ; 1
1  3 v x2x3.
3 v x2x3.