Минимизация числа состояний частичного автомата
Два частичных автомата называются совместимыми (слабо эквивалентными), если
1. они имеют одинаковое множество допустимых входных слов;
2. любое допустимое входное слово оба автомата перерабатывают в непротиворечивые выходные слова, при условии, что перед началом работы оба автомата находились в начальном состоянии.
Два выходных слова двух частичных автоматов A и A* называются непротиворечивыми, если все символы, которые определены в выходном слове автомата A совпадают со всеми соответствующими символами, которые определены в выходном слове автомата A*.
На рис. 3.16 приведен пример непротиворечивых выходных слов.
| p2 p3 p1 p2 |
| w2 w2 * w1 |
| A |
| p2 p3 p1 p2 |
| w2 * w1 w1 |
| A* |
Рис. 3.16
Два состояния s’ и s”частичного автомата называются совместимыми, если любое допустимое входное слово автомат перерабатывает в непротиворечивые выходные слова независимо от того какое из этих двух состояний было выбрано в качестве начального (s’ ~ s”).
Отношение совместимости обладает следующими свойствами:
1. рефлексивность, т.е. s’ ~ s’;
2. симметричность, т.е. если s’~ s”, то из этого следует: s”~ s’;
3. отсутствие транзитивности, т.е. если s’~ sk и s”~ sk, то из этого не следует, что: s’ ~ s”.
Отношение совместимости разбивает все множество состояний S на классы совместимости: S = Q1 U Q2 U Q3 U…U Qq.
Класс совместимости Qi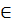 
S - это подмножество состояний попарно совместимых между собой, причем . Qi ∩ Qj ≠ Ø, если i ≠ j, т.е. пересечение любых двух классов совместимости не обязательно является пустым множеством и следовательно одно и то же состояние может входить в разные классы совместимости.
В общем случае число классов совместимости больше чем число классов эквивалентности и даже может и превышать исходных число состояний. Классы совместимости бывают простые и максимальные.
Простым классом совместимости называют подмножество состояний попарно совместимых между собой.
Максимальным классом совместимости называют класс, который не является подмножеством какого – либо другого класса совместимости.
Два необходимых условия совместимости состояний автомата Мили.
Два состояния s’ и s”являются совместимыми, если:
1. при переходе из этих состояний под воздействием любого одинакового входного символа pk функции выхода, если они определены должны совпадать, т.е: ψ’(s’,pk) = ψ”(s”,pk);
2. при переходе из этих состояний под воздействием любого одинакового входного символа pk переход, если он определен должен осуществляется в одно и то же или в совместимые состояния, т.е. если
si = φ’(s’,pk) и sj = φ”(s”,pk), то следует, что si ~ sj.
На рис. 3.17 приведен тривиальный пример совместимых состояний и их объединения. Состояния s’ ~ s”, так как из s’не определен переход по символу p1, а из состояния s” по символу p2.
| s’ |
| s” |
| sk |
| p1 / w1 |
| p2 / w2 |
| s’ |
| sk |
| p1 / w1 |
| p2 / w2 |
| ~ |
Рис. 3.17
Алгоритм минимизации числа состояний не полностью определенного (частичного) с помощью треугольной матрицы.
Минимизация числа состоянийзаключается в уменьшении числа состояний за счет объединения совместимых состояний.
Пусть задан таблицей переходов и выхода не полностью определенный автомат Мили, имеющий k –состояний.
Алгоритм состоит из выполнения следующих шагов:
1. строитсятреугольная матрица и аналогично, как в предыдущем алгоритме для полностью определенного автомата, определяются пары совместимых состояний;
2. формируются максимальные классы совместимости;
3. выбирается минимально необходимое число максимальных классов совместимости, для которых выполняются условия полноты и замкнутости;
4. если условия полноты и замкнутости выполняются для выбранного подмножества классов совместимости, то каждому классу совместимости присваивается символ нового состояния, а если не выполняются, то выбранное подмножества классов совместимости корректируется;
5. переписывается исходная таблица переходов так, чтобы при замене символа старого состояния на символ нового состояния не нарушилось условие замкнутости, далее объединяются строки таблицы, соответствующие совместимым состояниям.
Подмножество классов совместимости называется полным, если каждое состояние исходного автомата входит хотя бы в один из выбранных классов совместимости этого подмножества.
Подмножество классов совместимости называется замкнутым, если для любого его класса подмножество состояний, следующее за этим классом, целиком содержится хотя бы в одном из выбранныхклассов совместимости этого подмножества.
Проверка условия полноты производится с помощью таблицы покрытий, в которой столбцы соответствуют состояниям исходного автомата, а строки – выбранным классам совместимости.
Проверка условия замкнутости производится после нахождения подмножества состояний, следующих за каждым из выбранных классов совместимости. Для нахождения подмножества состояний E 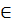S , следующее за подмножеством состояний D 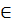S , необходимо определить по исходной таблице переходов подмножества состояний, в которые переходит автомат по одному и тому же входному символу из состояний подмножества D.
Если условие замкнутости не выполняется, то можно сузить какой либо класс совместимости не нарушая при этом условие полноты, удалить из него состояние, которое нарушает условие замкнутости, или расширить число выбранных классов совместимости, добавив новый класс совместимости необходимый для выполнения условия замкнутости. Для нового выбранного класса совместимости необходимо также проверить выполнения условия замкнутости.
Пример минимизации частичного автомата Мили заданного таблицей переходов и выхода (табл. 3.10).
P = { a , b , c , d , e }, W = {00 , 01 , 10 , 11}, S = {s1, s2, s3, s4, s5, s6, s7}.
В таблице переходов и выхода (табл. 3.10) для наглядности вместо символов состояний указаны только их индексы.
Таблица 3.10
| pk si | a | b | c | d | e |
| 1 / 00 | 5 / *1 | --- | --- | 6 / ** | |
| 5 / *0 | 4 / 0* | --- | --- | --- | |
| 4 / 11 | --- | --- | --- | 6 / 00 | |
| 6 / *1 | 6 / 00 | --- | 2 / 0* | --- | |
| --- | 7 / 0* | --- | 4 / *0 | --- | |
| --- | --- | 3 / *0 | --- | 2 / 10 | |
| --- | 2 / ** | 1 / 00 | --- | --- |
| 4,6 |
| 5,7 |
| 6,7 2,4 |
| 2,4 |
| 1,5 4,5 |
| 4,7 |
| 1,3 |
| 2,7 |
| 2,6 |
| 2,6 |
| 2,5 |
| 1 2 3 4 5 6 |
Рис. 3.18
На рис. 3.18 приведена треугольная матрица, заполненная по изложенному выше алгоритму. Клетки, не содержащие «×» соответствуют следующим парам совместимых состояний:
1 ~ 6, 1 ~ 7, 2 ~ 5, 2 ~ 6, 3 ~ 4, 3 ~ 5, 3 ~ 7, 4 ~ 6, 4 ~ 7, 5 ~ 6. и из них можно образовать следующие максимальные классы совместимости:
Строим дерево классов например, с помощью дерева, разбивая на каждом шаге множество состояний на два, одно из которых без состояний несовместимых с i–тым, другое не содержит само i–тое состояние (рис.3.19):
| {1 , 2 , 3 , 4 , 5 , 6 , 7} |
| {1 , 6 , 7} |
| { 2 , 3 , 4 , 5 , 6 , 7} |
| {2 , 5 , 6} |
| {2 , 5 , 6} |
| {2 , 5 , 6} |
| {3 , 4 , 5 , 6 , 7} |
| {3 , 4 , 5 , 7} |
| {3 , 4 , 7} |
| {3 , 5 , 7} |
| {3 , 4 , 7} |
| {3 , 5} |
| {3 , 7} |
| {4 , 5 , 6 , 7} |
| {4 , 6 , 7} |
| {5 , 6 , 7} |
| {5 , 6} |
| { 4, 6 } |
| {2 , 5 , 6 } |
| {1 , 6} |
| {1 , 7} |
| {1 , 6 , 7} |
| {1 , 6 , 7} |
| {1 , 6 , 7} |
| 1~ 2,3,4,5 |
| 2~ 3,4 |
| 3~ 6 |
| 4~ 5 |
Рис. 3.19
Получаются следующие максимальные классы Q1 = {1 , 6 },
Q2 = {1 , 7 }, Q3 = {2 , 5 , 6 }, Q4 = {3 , 4 , 7 }, Q5 = {3 , 5}, Q6 = {4 , 6}.
Для выполнения условия полноты достаточно выбрать следующее минимальное число максимальных классов совместимости :Q1 , Q3 , Q4 .
Для проверки условия замкнутости по таблице переходов определяются подмножества состояний следующих за выбранными классами совместимости (рис. 3.20).
a {1, - } a {5, -, - }
b {5, - } b {4, 7, - }
Q1 = {1 , 6 } c {-, 3 } Q3 = {2 , 5 , 6 } с { -, - , 3}
d { -, -} d {-, 4, - }
e {6, 2} e { -, - , 2}
a {4, 6, - }
b { -, 6, 2}
Q4 = {3 , 4 , 7 } c { -, - ,1}
d {-, 2, - }
e {6, -, - }
Рис. 3.20
Из рис. 3.20 видно, что подмножество {4, 7}, следующее по символу «b» за классом Q3 , входит в выбранный класс совместимости Q4 – это является соблюдением условия замкнутости.
Подмножество {4, 6}, следующее по символу «a» за классом Q4 , не входит ни в один из выбранных классов совместимости – это является нарушением условия замкнутости.
Для выполнения этого условия необходимо добавить класс совместимости Q6 = {4 , 6} и проверить для него выполнение условия замкнутости (рис.3.21).
a {6, - }
b {6, - }
Q6 = {4 , 6 } c {-, 3 }
d {2, -}
e {-, 2}
Рис.3.21
Добавление к выбранным классам нового класса Q6 не нарушает условия замкнутости (рис.3.21). Для упрощения перехода от старых состояний к новым, можно сузить класс Q1, удалив из него состояние s6, не нарушая условий полноты и замкнутости. В результате получается :
Q1 = { 1 }, Q3 = {2 , 5 , 6 }, Q4 = {3 , 4 , 7 }, Q6 = {4 , 6 }.
Каждому классу сопоставляется символ нового состояния:
Q1 – s’1, Q3 – s’2, Q4 – s’3, Q6 – s’4. Далее в исходной таблице переходов символ старого состояния, заменяется на символ нового состояния, который соответствует классу, в который это старое состояние входит, но с учетом выполнения условия замкнутости. В результате получается таблица переходов и выхода (табл. 3.11).
Таблица 3.11
| pk si | a | b | c | d | e |
| 1’ | 1’ / 00 | 2’ / *1 | --- | --- | 2’ / ** |
| 2’ | 2’ / *0 | 3’ / 0* | --- | --- | --- |
| 3’ | 4’ / 11 | 2’ / 00 | --- | --- | 2’/ 00 |
| 4’ | 4’ / *1 | 4’ / 00 | --- | 2’ / 0* | --- |
| 2’ | --- | 3’ / 0* | --- | 4’/ *0 | --- |
| 4’ | --- | --- | 3’ / *0 | --- | 2’ / 10 |
| 3’ | --- | 2’ / ** | 1’ / 00 | --- | --- |
После совмещения в ней строк, соответствующих совместимым состояниям, получается таблица переходов и выхода минимального автомата Мили (табл. 3.12), с числом состояний k* = 4 вместо k = 7 в исходном автомате.
Таблица 3.12
| pk si | a | b | c | d | e |
| 1’ | 1’ / 00 | 2’ / *1 | --- | --- | 2’ / ** |
| 2’ | 2’ / *0 | 3’ / 0* | 3’ / *0 | 4’/ *0 | 2’ / 10 |
| 3’ | 4’ / 11 | 2’ / ** | 1’ / 00 | 2’ / 0* | 4’ / 00 |
| 4’ | 4’ / *1 | 4’ / 00 | 3’ / *0 | 2’ / 0* | 2’ / 10 |
Для проверки правильности минимизации промоделируем работу обоих автоматов по переработке входного слова ecadabb.
Таблица 3.13
| tk | t0 | t1 | t2 | t3 | t4 | t5 | t6 | t7 |
| si | s1 | s6 | s3 | s4 | s2 | s5 | s7 | s2 |
| pj | e | c | a | d | a | b | b | |
| wm | ** | *0 | 0* | *0 | 0* | ** |
Таблица 3.14
| tk | t0 | t1 | t2 | t3 | t4 | t5 | t6 | t7 |
| s’i | s’1 | s’2 | s’3 | s’4 | s’2 | s’2 | s’3 | s’2 |
| p’j | e | c | a | d | a | b | b | |
| w’m | ** | *0 | 0* | *0 | 0* |
Результат работы исходного автомата приведен в табл. 3.13, а результат работы минимального автомата приведен в табл. 3.14. Получены непротиворечивые выходные слова, следовательно, минимизация проведена правильно.