Автомат без выходного преобразователя
Автомат без выходного преобразователя – это следующая совокупность четырех объектов: A = <P, S, s0 , φ>, где :
P = {p1, p2, …, pn} – входной алфавит;
S = {s0, s1, s2, …, sk} – множество состояний, в которых может находиться автомат;
s0 – начальное состояние автомата, s0 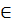 S;
S;
φ – функция перехода автомата, которое представляет собой отображение декартова произведения множеств P и S на множество S, т.е. P × S  S .
S .
Это значит что каждой паре: входной символ pi и состояние sj ставится в соответствие новое состояние sk. Функция перехода записывается следующим образом:
sk = φ(pi , sj), где:
pi – входной символ;
sj – текущее состояние автомата;
sk – новое состояние автомата.
Aбстрактный автомат называется конечным, если все его алфавиты конечны.
Автомат называется инициальным, если перед началом работы он должен быть установлен в начальное состояние s0.
Так как работа автомата рассматривается в дискретные моменты времени то функцию перехода можно представить в виде:
sk (t+1) = φ(pi(t) , sj(t)), где:
pi(t) и sj(t) – входной символ и состояние автомата в текущем автоматном такте (t);
sk (t+1) – новое состояние автомата в следующем автоматном такте (t+1).
Теория конечных автоматов не оперирует с такой величиной как время и символ t в приведенной формуле функции перехода обозначает текущий автоматный такт, а t+1 обозначает следующий автоматный такт.
Обычно в теории автоматов обозначения автоматных тактов при записи функций не указываются
Способы задания автомата без выходного преобразователя.
Пусть заданы: P – входной алфавит, S – множество состояний и s0 – начальное состояние автомата.
Существует три способа задания функций перехода:
1. перечислением;
2. табличный;
3. графический.
При перечислении приводятся все функции перехода:
s1 = φ(s0 , p1),
s2 = φ(s1 , p1),
. . . . . .
sk = φ(sk-1 , pn).
В табличном способе строится таблица переходов, столбцы которой помечаются входными символами, а строки – символами состояний из которых осуществляется переход. Внутри таблицы на пересечении i-той строки и j-того столбца указывается состояние, в которое переходит автомат из состояния si под воздействием входного символа pj.
Таблица 2.1
| pj si | p1 | p2 | ….. | pn |
| s0 | s1 | s2 | ….. | s1 |
| s1 | s2 | s2 | ….. | sk |
| ….. | ….. | ….. | ….. | .… |
| sk | ….. |
В графическом способе каждому состоянию автомата ставится в соответствие вершина графа, которая помечается символом этого состояния. Если из состояния si существует переход в состояние sj под воздействием входного символа pk, то вершины si и sj соединяются дугой, исходящей из si, а сама дуга помечается символом pk под воздействием которого осуществляется данный переход (рис.2.2). Направление дуги указывает направление перехода, поэтому граф автомата является ориентированным графом.
| si |
| sj |
| pk |
Рис. 2.2
Пример задания автомата без выходного преобразователя:
Пусть P = {p1, p2}, S = {s0, s1, s2}
Функцию перехода зададим тремя различными рассмотренными способами:
Перечислением: s0 = φ(s0 , p1), s1 = φ(s0 , p2), s1 = φ(s1 , p1), s2 = φ(s1 , p2),
s2 = φ(s2 , p1), s0 = φ(s2 , p2).
Таблицей переходов: (табл. 2.2).
Таблица 2.2
| pj si | p1 |
| ||
| s0 | s0 |
| ||
| s1 | s1 |
| ||
| s2 | s2 |
|
| p2 |
| s2 |
| p1 |
Рис. 2.3
В табл.2.3 приводится моделирование работы автомата, приведенного в примере, по переработке входного слова p1p2p2p1p2. В процессе работы происходит следующая смена состояний автомата: s0  s0
s0  s1
s1  s2
s2  s2
s2  s0, т.е. работа автомата без выходного преобразователя состоит в получении последовательности состояний.
s0, т.е. работа автомата без выходного преобразователя состоит в получении последовательности состояний.
Таблица 2.3
| Автоматный такт tk | t0 | t1 | t2 | t3 | t4 | t5 |
| Состояние автомата si | s0 | s0 | s1 | s2 | s2 | s0 |
| Входной символ pj | p1 | p2 | p2 | p1 | p2 |
2.4. Автомат с выходным преобразователем
Автомат с выходным преобразователем это есть совокупность следующих шести объектов:
A = <P , S , s0 , φ , W , ψ>, где:
P = {p1, p2, …, pn} – входной алфавит;
S = {s0, s1, s2, …, sk} – множество состояний;
s0 – начальное состояние автомата, s0 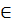 S;
S;
φ – функция перехода автомата;
W = {w1, w2, …, wm}– выходной алфавит;
ψ – функция выхода.
Определение объектов P , S , s0 , φ совпадает с определением тех же объектов в автомате без выходного преобразователя.
Существует две математические модели автомата с выходным преобразователем: автомат Мура и автомат Мили. Определение функции выхода ψ различно в каждой из этих моделей. Оба автомата можно представить в виде композиции автомата без выходного преобразователя A* и выходного преобразователя L.
Автомат Мура приведен на рис. 2.4, где:  ,
,  ,
,  слова из соответствующих алфавитов.
слова из соответствующих алфавитов.
  |
    |
 |
| A* A* A* A* |
| L L L L |
Рис.2.4
В автомате Мура функция выхода ψ осуществляет отображение множества S на множество W, т.е. S  W. Это означает что каждому состоянию si ставится в соответствие выходной символ wi. Функция перехода записывается следующим образом:
W. Это означает что каждому состоянию si ставится в соответствие выходной символ wi. Функция перехода записывается следующим образом:
wi = ψ(si), где:
si – текущее состояние автомата;
wi – выходной символ.
Существенным в определении функции выхода автомата Мура является то что новый выходной символ wi(t+1) в такте (t+1) определяется следующим состоянием si(t+1)) в которое переходит автомат. т.е. -
wi(t+1)= ψ(si(t+1)).
Автомат Мили приведен на рис. 2.5, где: A* – автомат без выходного преобразователя, L – преобразователь,  ,
,  ,
,  , – слова из соответствующих алфавитов.
, – слова из соответствующих алфавитов.
 |
 |
 |
| A* |
| L |
Рис.2.5
В автомате Мили функция выхода ψ осуществляет отображение декартова произведения множеств Pи S на множество W, т.е. P × S  W. Это значит что каждой паре: входной символ pi и состояние sj ставится в соответствие выходной символ wk. Функция выхода записывается следующим образом:
W. Это значит что каждой паре: входной символ pi и состояние sj ставится в соответствие выходной символ wk. Функция выхода записывается следующим образом:
wk = ψ(pi , sj), ), где:
pi – входной символ;
sj– текущее состояние автомата;
wk – выходной символ.
В функции выхода автомата Мили новый выходной символ wk(t+1) в такте (t+1) определяется входным символом pi(t) и состоянием si(t) в текущем такте (t).
wk(t+1) = ψ(pi(t) , sj(t)).
Способы задания автомата Мура.
Пусть заданы: P – входной алфавит, S – множество состояний, s0 – начальное состояние автомата и W – выходной алфавит.
Функции перехода и функции выхода могут быть представлены тремя способами:
1. перечислением;
2. табличный;
3. графический.
При перечислении приводятся все функции перехода и выхода:
s1 = φ (s0 , p1), w1 = ψ (s1),
s2 = φ (s1 , p1), w2 = ψ (s2),
. . . . . . . . . . . .
so = φ (sk , pn). w0 = ψ (s0).
В табличном способе строится таблица переходов, которая слева дополняется столбцом, в котором для каждого состояния sj указывается соответствующий ему выходной символ wj (табл.2.3).
В графическом способе каждому состоянию автомата ставится в соответствие вершина графа, которая помечается символом этого состояния si и выходным символом wi, соответствующим этому состоянию. Если из состояния si существует переход в состояние sj под воздействием входного символа pk, то вершины si и sj соединяются дугой исходящей из si, а сама дуга помечается символом pk под воздействием, которого осуществляется данный переход (рис.2.6).
Таблица 2.3
| wj | pi sj | p1 | p2 | ….. | pn |
| w0 | s0 | s1 | s2 | ….. | s1 |
| w1 | s1 | s2 | s2 | ….. | sk |
| ….. | ….. | ….. | ….. | ….. | .… |
| wk | sk | ….. | s0 |
| sj/wj |
| si/wi |
| pk |
Рис. 2.6
Пример автомата Мура.
Пусть P = {p1 , p2}, W = {w0 , w1}, S = {s0 , s1 , s2 , s3}.
Функции перехода : Функции выхода : s0 = φ (s0 , p1), w0 = ψ (s0),
s1 = φ (s0 , p2), w1 = ψ (s1),
s2 = φ (s1 , p1), w0 = ψ (s2),
s2 = φ (s2 , p1), w0 = ψ (s3).
s3 = φ (s1 , p2),
s3 = φ (s2 , p2),
s3 = φ (s3 , p1).
Таблица переходов и выхода заданного автомата Мура (табл.2.4).
Таблица 2.4
| wi | pi si | p1 | p2 |
| w0 | s0 | s0 | s1 |
| w1 | s1 | s2 | s3 |
| w0 | s2 | s2 | s3 |
| w0 | s3 | s3 | s0 |
Граф заданного автомата Мура (рис.2.7).
| s0 / w0 |
| s1 / w1 |
| s3 / w0 |
| s2 / w0 |
| p2 |
| p2 |
| p1 |
| p1 |
| p1 |
| p1 |
| p2 |
| p2 |
Рис.2.7
В табл.2.5 приводится моделирование работы автомата Мура, приведенного в примере, по преобразования входного слова p1p2p2p1p2. В процессе работы происходит следующая смена состояний автомата: s0  s0
s0  s1
s1  s3
s3  s3
s3  s0 и формируется следующая последовательность выходных символов w0w1w0w0w0, т.е. работа автомата Мура состоит в преобразования входного слова в выходное.
s0 и формируется следующая последовательность выходных символов w0w1w0w0w0, т.е. работа автомата Мура состоит в преобразования входного слова в выходное.
Таблица 2.5
| tk | t0 | t1 | t2 | t3 | t4 | t5 |
| si | s0 | s0 | s1 | s3 | s3 | s0 |
| pj | p1 | p2 | p2 | p1 | p2 | |
| wq | w0* | w0 | w1 | w0 | w0 | w0 |
В момент t0 значение wo* не учитывается, т.к. не является реакцией на входной символ, а определяется s0 - начальным состоянием автомата Мура еще до подачи на вход первого символа входной последовательности.
Способы задания автомата Мили
Пусть заданы: P – входной алфавит, S – множество состояний, s0 – начальное состояние автомата и W – выходной алфавит.
Функции перехода и функции выхода могут быть представлены тремя способами, как и в автомате Мура:
1. перечислением;
2. табличный;
3. графический.
При перечислении приводятся все функции перехода и выхода:
s1 = φ (s0 , p1), w1 = ψ (s0 , p1),
s2 = φ (s1 , p1), w2 = ψ (s1 , p1),
. . . . . . . . . . . .
so = φ (sk , pn). w0 = ψ (sk , pn).
Функция перехода задается как в автомате Мура. Отличие состоит в задании функции выхода.
В табличном способе строится таблица переходов (табл.2.6) и аналогичная ей таблица выходов (табл.2.7), на пересечении i - той строки и j - того столбца которой указывается выходной символ wk, который выдает автомат при переходе из состояния si под воздействием входного символа pj.
Таблица 2.6 Таблица 2.7
| pj si | p0 | p1 | … | pn |
| s0 | s1 | s2 | … | s3 |
| s1 | s2 | s3 | … | … |
| … | … | … | … | … |
| sк | s0 | … | … | sк |
| pj si | p0 | p1 | … | pn |
| s0 | w0 | w1 | … | wq |
| s1 | w1 | w2 | … | … |
| … | … | … | … | … |
| sк | w0 | … | … | wq |
Эти таблицы аналогичны, поэтому обычно они объединяются, и получается совмещенная таблица переходов и выхода (табл.2.8).
Таблица 2.8
| pj si | p0 | p1 | … | pn |
| s0 | s1/w0 | s2/w1 | … | s3/wq |
| s1 | s2/w1 | s3/w2 | … | … |
| … | … | … | … | … |
| sk | s0/w0 | … | … | sк/wq |
В графическом способе каждому состоянию автомата ставится в соответствие вершина графа, которая помечается символом этого состояния si. Если из состояния si существует переход в состояние sj под воздействием входного символа pk, то вершины si и sj соединяются дугой исходящей из si, а сама дуга помечается символом pk, под воздействием которого осуществляется данный переход и выходным символом wq, который вырабатывается при этом переходе (рис.2.8).
| si |
| sj |
| pk / wq |
Рис.2.8
Пример автомат Мили.
Пусть P = {p1 , p2}, W = {w0 , w1}, S = {s0 , s1 , s2}.
Функции перехода: Функции выхода:
s0 = φ( s0 , p1 ), w0 = ψ (s0 , p1),
s0 = φ( s2 , p2 ), w1 = ψ (s0 , p2),
s1 = φ( s0 , p2 ), w0 = ψ (s1 , p1),
s1 = φ( s1 , p1 ), w0 = ψ (s0 , p2),
s2 = φ( s1 , p2 ), w0 = ψ (s2 , p1),
s2 = φ( s2 , p1 ). w0 = ψ (s2 , p2).
Таблица переходов и выхода для заданного автомата Мили (табл.2.9).
Таблица 2.9
| pj si | p1 |
| ||
| s0 | s0/w0 |
| ||
| s1 | s1/w0 |
| ||
| s2 | s2/w0 |
|
| s2 |
| p2/w0 |
Граф заданного автомата Мили (рис.2.9).
| p1/w0 |
| p1/W0 |
В табл.2.10 приводится моделирование работы автомата Мили, приведенного в примере, по преобразования входного слова p1p2p2p1p2. В процессе работы происходит следующая смена состояний автомата: s0  s0
s0  s1
s1  s2
s2  s2
s2  s0 и формируется следующая последовательность выходных символов w0w1w0w0w0, т.е. работа автомата Мили состоит в преобразовании входного слова в выходное.
s0 и формируется следующая последовательность выходных символов w0w1w0w0w0, т.е. работа автомата Мили состоит в преобразовании входного слова в выходное.
Таблица 2.10
| tk | t0 | t1 | t2 | t3 | t4 | t5 |
| si | s0 | s0 | s1 | s2 | s2 | s0 |
| pj | p1 | p2 | p2 | p1 | p2 | |
| wq | w0 | w1 | w0 | w0 | w0 |
При сравнении работы автомата Мура (табл.2.5) и работы автомата Мили (табл.2.10) видно, что одно и то же входное слова p1p2p2p1p2 оба автомата перерабатывают в одно и то же выходное слова w0w1w0w0w0. Разница в работе автомата Мура и автомата Мили в том, что в автомате Мура выходной символ можно считывать сразу после установки его в начальное состояние, но при этом надо учитывать, что этот символ не является реакцией на входной символ, а определяется только начальным состоянием автомата Мура.
В автомате Мили выходной символ можно считывать после установки его в начальное состояние и подачи на его вход первого входного символа.
