Тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?

Решение:

1) Введём обозначения:

Z₂₈=(x & 28 = 0), Z₄₅=(x & 45 = 0), Z₄₈=(x & 48 = 0), A = (x & a = 0)

2) перепишем исходное выражение и преобразуем его, используя свойство импликации:

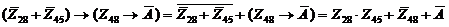
3) перейдем к импликации, используя закон де Моргана:

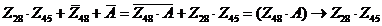
4) преобразуем выражение в правой части по формуле 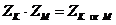, выполнив поразрядную дизъюнкцию (операцию ИЛИ):

28 = 011100

45 = 101101

28 or 45 = 111101 = 61

получаем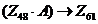

5) для того, чтобы выражение 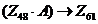было истинно для всех x, нужно, чтобы двоичная запись числа 48 or a содержала все единичные биты числа 61. Таким образом, с помощью числа a нужно добавить те единичные биты числа 61, которых «не хватает» в числе 48:

48 = 110000

a = **11*1

61 = 111101

биты, обозначенные звездочками, могут быть любыми.

6) поскольку нас интересует минимальное значение a, все биты, обозначенные звездочкой, можно принять равными нулю.

7) получается A = 2³ + 2² + 2⁰ = 13

8) Ответ: 13.

Р-20 (М.В. Кузнецова).Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула

ДЕЛ(x, А) ® (ДЕЛ(x, 21) + ДЕЛ(x, 35))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Решение:

1) введём обозначения A = ДЕЛ(x, А), D₂₁ = ДЕЛ(x, 21) , D₃₅ = ДЕЛ(x, 35)

2) введём множества:

A –множество натуральных чисел, для которых выполняется условие A

D₂₁ –множество натуральных чисел, для которых выполняется условие D₂₁

D₃₅ –множество натуральных чисел, для которых выполняется условие D₃₅

…

3) Запишем формулу из условия в наших обозначениях

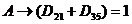
4) Раскроем импликацию по правилу :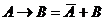

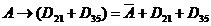
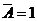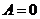5) Чтобы формула была тождественно истинной необходимо, чтобы (т.е. ), когда . Тогданаибольшее множество А определяется как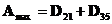

6) Множество 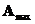, точно соответствующее выражению с помощью функции ДЕЛполучить невозможно.

7) Выполним анализ исходной формулы с помощью кругов Эйлера.

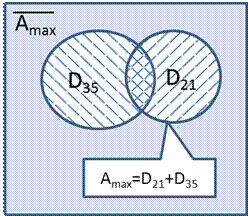
Чтобы в множество 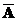входили все числа, не попавшие в объединение 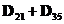, достаточно, чтобы множество А находилось внутри этого объединения, например, совпадая с одним из множеств D₃₅ или D₂₁, или располагаясь внутри любого из них, что возможно, если использовать делители, кратные 21 или 35.

8) В задании требуется найти НАИМЕНЬШЕЕ значение, этому условию соответствует 21.

9) Ответ: 21

Ещё пример задания:

Р-19 (М.В. Кузнецова).Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула

ДЕЛ(x, А) ® (ДЕЛ(x, 21) Ù ДЕЛ(x, 35))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Решение:

1) введём обозначения A = ДЕЛ(x, А), D₂₁ = ДЕЛ(x, 21) , D₃₅ = ДЕЛ(x, 35) иD_N = ДЕЛ(x, N)

2) введём множества:

A –множество натуральных чисел, для которых выполняется условие A

D₂₁ –множество натуральных чисел, для которых выполняется условие D₂₁

D₃₅–множество натуральных чисел, для которых выполняется условие D₃₅

…

3) Запишем формулу из условия в наших обозначениях

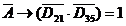
4) Раскроем импликацию по правилу :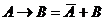

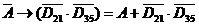
5) Чтобы формула была тождественно истинной необходимо, чтобы А = 1, когда 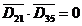. Тогдамножество А определяется так: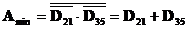

6) Множество 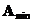, точно соответствующее выражению с помощью функции ДЕЛполучить невозможно.

7) Выполним анализ исходной формулы с помощью кругов Эйлера.

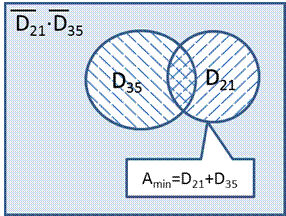
в множество А должны входить все числа, попавшие в объединение 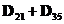. Нужно найти множество, в которое входят оба эти множества. Для этого рассмотрим делители чисел 21 и 35.

8) Число 35 делится на 5 и 7, поэтому: 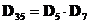, 21 делится на 3 и 7, поэтому: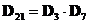

9) Перепишем и упростим формулу для А: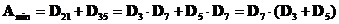

10) Таким образом, каждое из множеств D₃₅ и D₂₁ входит в множество D₇ . Объединение D₃₅ + D₂₁ тоже входит в D₇. Поскольку 7 – наибольший общий делитель чисел 21 и 35, то найдено максимальное значение соответствующее условию задачи.

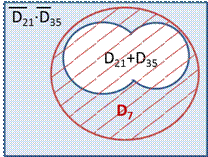
11) Ответ: 7.

Р-14.Элементами множества А являются натуральные числа. Известно, что выражение

(x Î {2, 4, 6, 8, 10, 12}) → (((x Î {4, 8, 12, 116}) Ù (x Î A)) → (x Î {2, 4, 6, 8, 10, 12}))

истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение суммы элементов множества A.

Решение:

1) Заметим, что в задаче, кроме множества A, используются еще два множества:

P = {2, 4, 6, 8, 10, 12} Q = {4, 8, 12, 116}

2) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами

A: x Î А, P: x Î P, Q: x Î Q

3) перейдем к более простым обозначениям

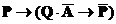
4) раскрываем обе импликации по формуле :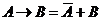

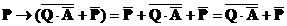
5) теперь используем закон де Моргана :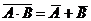

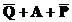
6) поскольку это выражение должно быть равно 1, то A должно быть истинным везде, где ложно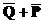

7) тогда минимальное допустимое множество A – это 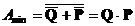(по закону де Моргана)

8) переходим ко множествам

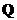= {4, 8, 12, 116}

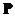= {2, 4, 6, 8, 10, 12}

9) тогда 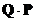– это все натуральные числа, которые входят одновременно в 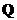и 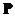; они выделены жёлтым цветом: {4, 8, 12}

10) именно эти числа и должны быть «перекрыть» множеством А_min, поэтому минимальный состав множества A – это А_min = {4, 8, 12}, сумма этих чисел равна 24

11) Ответ: 24.

Решение (3 способ, А.В. Лаздин, НИУ ИТМО):

1) обозначим множества следующим образом:

L = {2, 4, 6, 8, 10, 12} M = {4, 8, 12, 116}.
тогда исходное выражение можно записать в упрощенной форме:

(x Î L) →(((x Î M) Ù (x Î A)) →(x Î L)) (1)

2) если х не принадлежит множеству L, то выражение принимает значение 1, независимо от множества А (импликация из 0 всегда равна 1); таким образом, необходимо рассмотреть ситуацию, когда x Î L.

3) Условие 1. x Î {2, 4, 6, 8, 10, 12}

В этом случае исходное выражение принимает следующий вид:

1 →(((x Î M) Ù (x Î A)) → 0) (2)

это выражение примет значение 0 только в том случае, если

(((x Î M) Ù (x Î A)) → 0) будет ложным.
Для этого выражение ((x Î M) Ù (x Î A)) должно быть истинным (импликация из 1 в 0).

4) если х не принадлежит множеству М, то выражение 2 будет истинным не зависимо от множества А.

5) таким образом множество А влияет на решение задачи только при одновременном соблюдении двух условий:

1. x Î {2, 4, 6, 8, 10, 12}

2. x Î {4, 8, 12, 116}

В этом случае исходное выражение принимает следующий вид:

1 →((1 Ù (x Î A)) → 0) (3)

6) для того чтобы это выражение было истинным, выражение (x Î A) обязательно должно быть ложным; для этого выражение x Î A должно быть истинным.

7) значит, одновременно должны быть выполнены три условия:

1. x Î {2, 4, 6, 8, 10, 12}

2. x Î {4, 8, 12, 116}

3. x Î A

для этого множеству А обязательно должны принадлежать числа 4, 8, 12.

8) Ответ: 24.

Пример задания:

Р-13.На числовой прямой даны два отрезка: P = [37; 60] и Q = [40; 77]. Укажите наименьшую возможную длину такого отрезка A, что формула

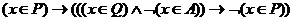
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Решение:

1) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами

A: x Î А, P: x Î P, Q: x Î Q

2) перейдем к более простым обозначениям

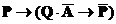
3) раскрываем обе импликации по формуле :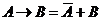

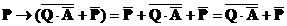
4) теперь используем закон де Моргана :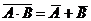

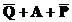
5) в таком виде выражение уже смотрится совсем не страшно; Сразу видно, что отрезок 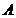должен перекрыть область на числовой оси, которая не входит в область :

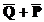6) по рисунку видно, что не перекрыт только отрезок [40;60] (он выделен жёлтым цветом), его длина – 20, это и есть правильный ответ.

7) Ответ: 20.

Ещё пример задания:

Р-12.На числовой прямой даны два отрезка: P = [10,39] и Q = [23, 58]. Выберите из предложенных вариантов такой отрезок A, что логическое выражение

((x Î P) Ù (x Î A) ) → ((x Î Q) Ù (x Î A) )

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) [5, 20] 2) [15, 35] 3) [25, 45] 4) [5, 65]

Решение:

1) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами

A: x Î А, P: x Î P, Q: x Î Q

2) перейдем к более простым обозначениям

P ×A → Q ×A

3) раскроем импликацию через операции НЕ и ИЛИ ( ):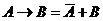

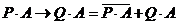
4) раскроем инверсию первого слагаемого по закону де Моргана ( ):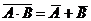

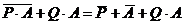
5) теперь применим закон поглощения

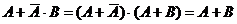
к последним двум слагаемым:

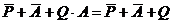
6) для того, чтобы выражение было истинно при всех x, нужно, чтобы 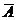было истинно там, где ложно 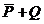, то есть там, где истинно 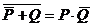(жёлтая область на рисунке)

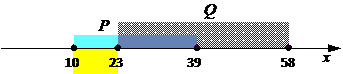
7) таким образом, A должно быть ложно на отрезке [10,23], такое отрезок в предложенном наборе один – это отрезок [25, 45]

8) Ответ: 3.

Ещё пример задания:

Р-11.На числовой прямой даны два отрезка: P = [10,30] и Q = [25, 55]. Определите наибольшую возможную длину отрезка A, при котором формула

( x Î A) → ((x Î P) Ú (x Î Q) )

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) 10 2) 20 3) 30 4) 45

Решение:

1) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами

A: x Î А, P: x Î P, Q: x Î Q

2) перейдем к более простым обозначениям

A → (P + Q)

3) раскроем импликацию через операции НЕ и ИЛИ ( ):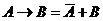

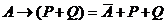
4) для того, чтобы выражение было истинно при всех x, нужно, чтобы 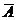было истинно там, где ложно 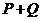(жёлтая область на рисунке)

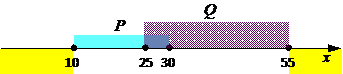
5) поэтому максимальный отрезок, где A может быть истинно (и, соответственно, 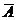ложно) – это отрезок [10,55], имеющий длину 45

6) Ответ: 4.

Ещё пример задания:

Р-10.На числовой прямой даны два отрезка: P = [10,20] и Q = [25, 55]. Определите наибольшую возможную длину отрезка A, при котором формула

( x Î A) → ((x Î P) Ú (x Î Q) )

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) 10 2) 20 3) 30 4) 45

Решение:

1) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами

A: x Î А, P: x Î P, Q: x Î Q

2) перейдем к более простым обозначениям

A → (P + Q)

3) раскроем импликацию через операции НЕ и ИЛИ ( ):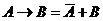

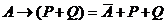
4) для того, чтобы выражение было истинно при всех x, нужно, чтобы 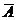было истинно там, где ложно 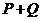(жёлтая область на рисунке)

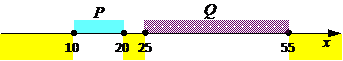
5) поскольку области истинност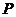и и 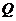разделены, максимальный отрезок, где A может быть истинно (и, соответственно, 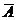ложно) – это наибольший из отрезков 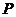и 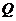, то есть отрезок [25,55], имеющий длину 30

6) Ответ: 3.

Ещё пример задания:

Р-09.На числовой прямой даны два отрезка: P = [14,34] и Q = [24, 44]. Выберите такой отрезок A, что формула

( x Î A) → ((x Î P) º (x Î Q) )

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Если таких отрезков несколько, укажите тот, который имеет большую длину.

1) [15, 29] 2) [25, 29] 3) [35,39] 4) [49,55]

Решение:

1) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами

A: x Î А, P: x Î P, Q: x Î Q

2) перейдем к более простым обозначениям

A → (P º Q)

3) выражение R = (P º Q) истинно для всех значений x, при которых P и Qравны (либо оба ложны, либо оба истинны)

4) нарисуем область истинности выражения R = (P º Q)на числовой оси (жёлтые области)

5) импликация A → R истинна за исключением случая, когда A=1 и R=0, поэтому на полуотрезках [14,24[ и ]34,44], где R=0, выражение A должно быть обязательно ложно; никаких других ограничений не накладывается

6) из предложенных ответов этому условия соответствуют отрезки [25,29] и [49,55]; по условию из них нужно выбрать самый длинный

7) отрезок [25,29] имеет длину 4, а отрезок [49,55] – длину 6, поэтому выбираем отрезок [49, 55]

8) Ответ: 4.

Ещё пример задания:

Р-08.На числовой прямой даны два отрезка: P = [20, 50] и Q = [10, 60]. Выберите такой отрезок A, что формула

( (x Î P) → (x Î А) ) /\ ( (x Î A) → (x Î Q) )

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Если таких отрезков несколько, укажите тот, который имеет большую длину.

1) [5, 40] 2) [15, 54] 3) [30,58] 4) [5, 70]

Решение:

1) в этом выражении две импликации связаны с помощью операции И (конъюнкции), поэтому для истинности всего выражения обе импликации должны быть истинными

2) для того, чтобы упростить понимание выражения, обозначим отдельные высказывания буквами

A: x Î А, P: x Î P, Q: x Î Q

3) перейдем к более простым обозначениям в обоих условиях

(P → A)/\ (A → Q)

и выразим импликацию через операции ИЛИ и НЕ:

,

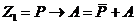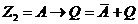
4) выражение должно быть истинно на всей числовой оси; обозначим область, которую перекрывает выражение 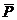– это две полуоси

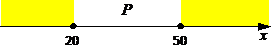
5) отсюда следует, что отрезок A должен полностью перекрывать отрезок P; этому условию удовлетворяют варианты ответов 2 и 4

6) выражение 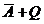тоже должно быть истинно на всей числовой оси; выражение 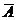должно перекрывать все, кроме отрезка, который перекрывает выражение :

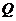7) поэтому начало отрезка 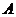должно быть внутри отрезка [10,20], а его конец – внутри отрезка [50,60]

8) этим условиям удовлетворяет только вариант 2.

9) Ответ: 2.

[1] Огастес (Август) де Морган –шотландский математик и логик.

[2] http://kpolyakov.spb.ru/download/bitwise2.pdf