Задачи с поразрядными операциями

Повышенный уровень, время – 3 мин)

Тема: Основные понятия математической логики.

Про обозначения

К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (Ù,Ú,), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает Ù и Ú. Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù, Ú,), что еще раз подчеркивает проблему. Далее во всех решениях приводятся два варианта записи.

Что нужно знать:

· условные обозначения логических операций

A, 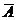не A (отрицание, инверсия)

A Ù B, A и B (логическое умножение, конъюнкция)

A Ú B, A или B (логическое сложение, дизъюнкция)

A→B импликация (следование)

· таблицы истинности логических операций «И», «ИЛИ», «НЕ», «импликация» (см. презентацию «Логика»)

· операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:

A→B = A Ú Bили в других обозначениях A→B =

· если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», и самая последняя – «импликация»

· иногда полезны формулы де Моргана[1]:

(A Ù B) = A Ú B

(A Ú B) = A Ù B

· для упрощения выражений можно использовать формулы

(т.к. )
(т.к. )

· некоторые свойства импликации

Связь логики и теории множеств:

· пересечение множеств соответствует умножению логических величин, а объединение – логическому сложению;

· пустое множество Æ – это множество, не содержащее ни одного элемента, оно играет роль нуля в теории множеств;

· универсальное множество I – это множество, содержащее все возможные элементы заданного типа (например, все целые числа), оно играет роль логической единицы: для любого множества целых чисел X справедливы равенства X + I = I и X · I = X (для простоты мы используем знаки сложения и умножения вместо знаков пересечения Ç и объединения È множеств)

· дополнение множества X – это разность между универсальным множеством I и множеством X (например, для целых чисел – все целые числа, не входящие в X)

· пусть требуется выбрать множество A так, чтобы выполнялось равенство A + X = I; в этом случае множество A должно включать дополнение , то есть (или «по-простому» можно записать ), то есть

· пусть требуется выбрать множество A так, чтобы выполнялось равенство , в этом случае множество 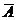должно включать дополнение , то есть ; отсюда , то есть

Задачи с поразрядными операциями

Повышенный уровень, время – 3 мин)

Тема: Основные понятия математической логики.

Про обозначения

К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (Ù,Ú,), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает Ù и Ú. Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù, Ú,), что еще раз подчеркивает проблему. Далее во всех решениях приводятся два варианта записи.

Что нужно знать:

· условные обозначения логических операций

A, 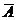не A (отрицание, инверсия)

A Ù B, A и B (логическое умножение, конъюнкция)

A Ú B, A или B (логическое сложение, дизъюнкция)

A→B импликация (следование)

· таблицы истинности логических операций «И», «ИЛИ», «НЕ», «импликация» (см. презентацию «Логика»)

· операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:

A→B = A Ú Bили в других обозначениях A→B =

· если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», и самая последняя – «импликация»

· иногда полезны формулы де Моргана[1]:

(A Ù B) = A Ú B

(A Ú B) = A Ù B

· для упрощения выражений можно использовать формулы

(т.к. )
(т.к. )

· некоторые свойства импликации

Связь логики и теории множеств:

· пересечение множеств соответствует умножению логических величин, а объединение – логическому сложению;

· пустое множество Æ – это множество, не содержащее ни одного элемента, оно играет роль нуля в теории множеств;

· универсальное множество I – это множество, содержащее все возможные элементы заданного типа (например, все целые числа), оно играет роль логической единицы: для любого множества целых чисел X справедливы равенства X + I = I и X · I = X (для простоты мы используем знаки сложения и умножения вместо знаков пересечения Ç и объединения È множеств)

· дополнение множества X – это разность между универсальным множеством I и множеством X (например, для целых чисел – все целые числа, не входящие в X)

· пусть требуется выбрать множество A так, чтобы выполнялось равенство A + X = I; в этом случае множество A должно включать дополнение , то есть (или «по-простому» можно записать ), то есть

· пусть требуется выбрать множество A так, чтобы выполнялось равенство , в этом случае множество 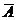должно включать дополнение , то есть ; отсюда , то есть

Задачи с поразрядными операциями