Логические операции и таблицы истинности:25 вопрос

p	q	Øp	Øq	p&q	ØpÚØq	Ø(ØpÚØq)	(p&q) É Ø(ØpÚØq)

В данной таблице всего четыре строки, поскольку формула содержит лишь две переменные – p и q. Первые два столбца задают все возможные комбинации совместной истинности и ложности этих переменных. Следующие пять столбцов показывают, каким будет значение каждой подформулы в той или иной строчке. Последний (результирующий) столбец показывает значение всей формулы в целом.

В зависимости от того, каким является результирующий столбец таблицы, выделяют три вида формул: тождественно-истинные, тождественно-ложные и логически случайные.

Тождественно-истинной (общезначимой) называется формула, принимающая значение «1» во всех строках таблицы.

Тождественно-ложной (невыполнимой) называется формула, принимающая значение «0» во всех строках таблицы.

Логически случайной (собственно выполнимой) называется формула, принимающая в некоторых строках таблицы значение «1», а в некоторых – «0».

В приведенном примере формула является тождественно-истинной. Она истинна всегда, независимо от того, истинны или ложны входящие в нее пропозициональные переменные. Другими словами, данная формула выражает собой логический закон.

27.Основные способы правильных умозаключений КЛВ, их характеристика.

28.Принципы логической семантики и ошибки, связанные с их нарушением.

Булевы операции над объемами понятий.

Операции над понятиями, точнее – над объемами понятий, то есть классами называются булевыми, по имени английского логика Дж. Буля, построившего особую алгебру логики, получившую в его честь название булевой алгебры.

Предположим, что даны два понятия aА(a)иaВ(a). Условимся, что род у этих понятий один и тот же. Объемы этих понятий будем сокращенно обозначать просто буквами А и В (читается: «класс А» и «класс В»). Тогда с этими объемами можно осуществить следующие операции:

а) пересечение (АÇВ) б) объединение (АÈВ)

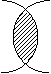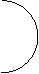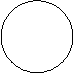
А В А В

в) вычитание (А\В) г) взятие дополнения (ØА)

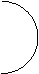А В А ØA

Штриховкой на схемах обозначен результат применения соответствующих операций к классам А и В.

Пересечение объемов двух понятий равняется классу предметов, которые входят одновременно в объем каждого из них. Объединение двух понятий равняется классу предметов, которые входят в объем по крайней мере одного из них. Вычитание объема одного понятия из объема другого равняется классу предметов, которые входят в объем первого понятия, но не входят в объем второго. Дополнение к объему понятия представляет собой класс предметов, которые не входят в объем этого понятия.

Основные законы булевой алгебры, их характеристика.

31.Логические отношения между сложными суждениями.