ВОПРОС 32 (Дедуктивные умозаключения и их виды.)

Дедуктивные умозаключения – вид умозаключений, в котором из посылок, выражающих знания большей степени общности, необходимо следует заключение, выражающее знание меньшей степени общности. Дедукция в переводе с латинского означает "выведение".
Пример: "Ни один смертный не может до конца постичь замысел Бога. Все люди смертны. Ни один человек не может до конца понять замысел Бога".
Виды дедуктивных умозаключений:

1) непосредственные умозаключения

2) силлогизмы – умозаключения, в которых из двух суждений выводится третье.

Непосредственные умозаключения – это заключения, выводимые из одной посылки. Этот вид умозаключений позволяет уточнить отношения объёмов понятий, входящих в суждения. Непосредственные умозаключения – это превращение, обращение, противопоставление предикату и умозаключение по логическому квадрату.

Категорический силлогизм – вид дедуктивного умозаключения, в котором из двух истинных категорических суждений, связанных средним термином, при соблюдении правил вывода необходимо следует заключение.
Понятия, входящие в состав силлогизма, называются терминами силлогизма. В простом категорическом силлогизме только 3 термина:
больший термин (Р) – предикат заключения; большая посылка
меньший термин (S) – субъект заключения; меньшая посылкака
средний термин (М) – связывает в посылках Р и S, в заключении отсутствует.

ВОПРОС 33 (Простой категорический силлогизм. Фигуры и модусы фигур простого категорического силлогизма)

Простой категорический силлогизм

Понятия, входящие в состав силлогизма, называются терминами силлогизма. В простом категорическом силлогизме только 3 термина:больший термин (Р) – предикат заключения; большая посылкаменьший термин (S) – субъект заключения; меньшая посылкака
средний термин (М) – связывает в посылках Р и S, в заключении отсутствует.

Структуру простого категорического силлогизма составляют две посылки и заключение.Все жидкости (М) – упруги (Р) – большая посылкаРтуть (S) – жидкость (М) – меньшая посылкаРтуть (S) – упруга (Р) – заключение

Фигуры и модусы простого категорического силлогизма

Фигурами категорического силлогизма называются формы силлогизма, различающиеся по положению среднего термина (М) в посылках.

1 фигура	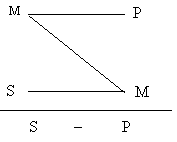Большая посылка – общая, меньшая посылка – утвердительная.	Все злаки (М) – растения (Р) Рожь (S) – злак (М) Рожь (S) – растение (P)
2 фигура	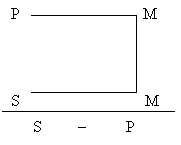Большая посылка – общая, одна из посылок – отрицательная.	Все ужи (Р) – пресмыкающиеся (М) Это животное (S) – не пресмыкающееся (М) Это животное (S) – не уж (Р)
3 фигура	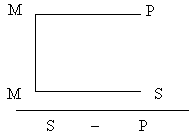Меньшая посылка – утвердительная, заключение – частное.	Все углероды (М) – простые тела (Р) Все углероды (М) – электропроводники (S) Некоторые электропроводники (S) – простые тела (Р)
4 фигура	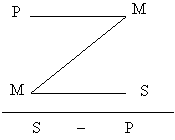Заключение не может быть общеутвердительным суждением.	Все киты (Р) – млекопитающие (М) Ни одно млекопитающее (М) – не рыба (S) Ни одна рыба (S) – не кит (Р)

В каждой фигуре возможно несколько допустимых (правильных) сочетаний посылок и заключения. Такие сочетания называются модусами.
Модусы фигур категорического силлогизма – разновидности силлогизма, отличающиеся друг от друга качественной и количественной характеристикой входящих в них посылок и заключений.

ВОПРОС 34 (Общие правила простого категорического силлогизма)

Общие правила простого категорического силлогизм:

Правила терминов

1. В силлогизме должно быть только три термина (S, P, M).

2. Средний термин должен быть распределён по крайней мере в одной из посылок.

3. Термин в заключении может быть распределён только тогда, когда он распределён в посылке.

Правила посылок

1. Из двух отрицательных посылок вывод не производится.

2. Если одна из посылок отрицательная, то и заключение должно быть отрицательным.

3. Из двух частных посылок нельзя сделать вывод.

4. Если одна из посылок частная, то заключение должно быть частным.

ВОПРОС 35 (Специальные правила фигур силлогизма)