Конъюнктивные формы представления логических функций

Введем понятие элементарной дизъюнкции.

Элементарной дизъюнкцией называется выражение вида

,

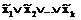содержащее множество попарно различных переменных или их отрицаний.

Конъюнктивной нормальной формой (КНФ) логической функции называется конъюнкция любого конечного множества попарно различных элементарных дизъюнкций. Например, логические функции

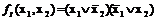
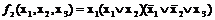
представляют собой конъюнкции элементарных дизъюнкций. Следовательно, они записаны в конъюнктивной нормальной форме.

Произвольная логическая функция, заданная аналитическим выражением, может быть приведена к КНФ путем выполнения следующих операций:

- использования правила инверсии, если операция отрицания применена к логическому выражению;

-использования аксиомы дистрибутивности относительно умножения:

;

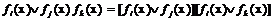-использования операции поглощения:

;

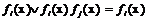- исключения в дизъюнкциях повторяющихся переменных или их отрицаний;

- удаления всех одинаковых элементарных дизъюнкций, кроме одной;

-удаления всех дизъюнкций, в которые одновременно входят переменная и ее отрицание.

Справедливость перечисленных операций вытекает из основных аксиом и тождественных соотношений алгебры логики.

Конъюнктивная нормальная форма называется совершенной, если каждая входящая в нее элементарная дизъюнкция содержит в прямом или инверсном виде все переменные, от которых зависит функция.

Преобразование КНФ к совершенной КНФ осуществляется путем выполнения следующих операций:

- прибавления к каждой элементарной дизъюнкции конъюнкций переменных и их отрицаний, если они не входят в данную элементарную дизъюнкцию;

- использования аксиомы дистрибутивности;

-удаление всех одинаковых элементарных дизъюнкций, кроме одной.

В совершенной КНФ может быть представлена любая логическая функция, кроме

тождественно равной единице ( 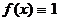). Отличительным свойством совершенной КНФ является то, что представление в ней логической функции единственно.

Элементарные дизъюнкции, входящие в совершенную КНФ функции, носят название конституент нуля. Каждая конституента нуля, входящая в совершенную КНФ, обращается в нуль на единственном наборе значений переменных, который является нулевым набором функции. Следовательно, число нулевых наборов логической функции совпадает с числом конституент нуля, входящих в ее совершенную КНФ.

Логическая функция константа нуля в совершенной КНФ представляется конъюнкцией 2nконституент нуля. Сформулируем правило составления СКНФ логической функции по таблице соответствия.

Для каждой строки таблицы соответствия, в которой функция равна нулю, составляется элементарная дизъюнкция всех переменных. При этом в дизъюнкцию входит сама переменная, если ее значение равно нулю, или отрицание, если ее значение равно единице. Полученные элементарные дизъюнкции объединяются знаком конъюнкции.

Пример 3.4.Для логической функции z(x), заданной таблицей соответствия 2.2, определим совершенную конъюнктивную форму.

Для первой строки таблицы, которая соответствует нулевому набору функции 000, находим конституенту нуля 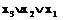. Выполнив аналогичные операции для второй, третьей и пятой строк, определим искомую совершенную КНФ функции:

.

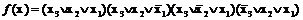Необходимо отметить, что для функций, число единичных наборов которых превышает число нулевых наборов, более компактной является их запись в виде СКНФ и наоборот.