Дизъюнктивные формы представления логических функций
Одним из основных способов задания логических функций является их представление в виде аналитических выражений (формул). Достоинством такого способа задания является возможность проведения эквивалентных преобразований логических функций. Во введенной алгебре (3.1) основными аналитическими формами представления логических функций являются дизъюнктивная и конъюнктивная формы.
Рассмотрим дизъюнктивные формы представления логических функций.
Предварительно введем понятие элементарной конъюнкции.
Элементарной конъюнкцией называется выражение вида
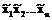 ,
,
содержащее множество попарно различных переменных или их отрицаний. При этом под х поднимается либо сама переменная х, либо ее отрицание х.
Дизъюнктивной нормальной формой (ДНФ) логической функции называется дизъюнкция любого конечного множества попарно различных элементарных конъюнкций. Например, логические функции
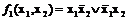 ;
;
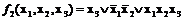
представляют собой дизъюнкции элементарных конъюнкций. Следовательно, они записаны в дизъюнктивной форме.
Произвольная логическая функция, заданная аналитическим выражением, может быть приведена к ДНФ путем:
- использования правил инверсии, если операция отрицания применена к логическому выражению;
- раскрытия скобок;
- исключения в конъюнкциях повторяющихся переменных или их отрицаний;
- удаление всех одинаковых элементарных конъюнкций, кроме одной;
- исключение всех конъюнкций, в которых одновременно содержатся переменная и ее отрицание.
Справедливость перечисленных операций вытекает из основных аксиом и тождественных соотношений алгебры логики.
Пример 3.1. Преобразуем к дизъюнктивной нормальной форме логическую функцию: 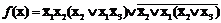 .
.
Используем правило инверсии. Тогда
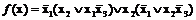 .
.
Раскроем в полученном выражении скобки
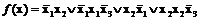
и исключим повторяющиеся конъюнкции и конъюнкции, содержащие как переменную так и ее отрицание, а также повторяющиеся одинаковые переменные, входящие в конъюнкцию. В результате выполнения перечисленных операций получаем ДНФ функции
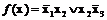 .
.
Дизъюнктивная нормальная форма называется совершенной (СДНФ), если каждая входящая в нее элементарная конъюнкция содержит в прямом или инверсном виде все переменные, от которых зависит функция.
Преобразование ДНФ к совершенной форме ДНФ осуществляется путем выполнения следующих операций:
- умножения каждой элементарной конъюнкции на дизъюнкции переменных и их отрицаний, если они не входят в данную элементарную конъюнкцию;
- раскрытия скобок;
- удаления всех одинаковых элементарных конъюнкций, кроме одной.
Пример 3.2.Преобразуем к СДНФ логическую функцию
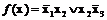 .
.
Так как рассматриваемая функция зависит от трех переменных х1, х2, х3, первую конъюнкцию умножим на выражение 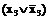 , а вторую - на
, а вторую - на 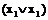 :
:
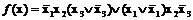 .
.
Раскрыв скобки и исключив повторяющиеся конъюнкции, получим искомую совершенную дизъюнктивную нормальную форму функции:
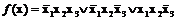 .
.
В СДНФ может быть представлена любая логическая функция, кроме тождественно равной нулю (f(x)º0).
Отличительным свойством СДНФ является то, что представление в ней логической функции единственно.
Элементарные конъюнкции, входящие в СДНФ функции, носят название конституент единицы. Так как конституента единицы содержит в прямом или инверсном виде все переменные, от которых зависит функция, то она обращается в единицу на единственном наборе значений переменных. Отсюда следует, что каждая СДНФ содержит столько конституент единицы, сколько единичных наборов имеет логическая функция. Так, функция, рассмотренная в примере 3.2, задана на трех единичных наборах, следовательно, ее СДНФ содержит три конституенты единицы.
Логическая функция константы единицы в СДНФ представляется дизъюнкцией 2n конституент единицы.
В практических задачах при первичном описании логические функции чаще всего задаются таблицами соответствия, в которой каждому набору сопоставляется конституента единицы. При этом в конституенту единицы входит переменная, если ее значение в наборе равно единице, и инверсия переменной, если ее значение в наборе равно нулю. Логическая функция содержит столько конситуент единицы, сколько рабочих наборов задано в таблице соответствия. Отсюда следует правило определения совершенной СДНФ функции по таблице соответствия.
Для каждой строки таблицы, в которой функция равна единице, составляется элементарная конъюнкция всех переменных. При этом в конъюнкцию входит сама переменная, если ее значение равно единице, или отрицание если ее значение равно нулю. Полученные элементарные конъюнкции объединяются знаком дизъюнкции.
Пример 3.3.Для логической функции z(х), заданной таблицей соответствия 2.2, определим совершенную дизъюнктивную нормальную форму.
Для четвертой строки таблицы, которая соответствует единичному набору функции 011, найдем конституенту единицы `х3х2х1.
Выполнив логические операции для шестой, седьмой и восьмой строк, определим искомую СДНФ функции:
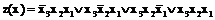 .
.
Таким образом, СДНФ логических функций получается путем использования операций и аксиом алгебры логики.
