Реализация логических функций на цифровых интегральных схемах

Все возрастающая сложность цифровых устройств привела к созданию микроминиатюрных интегральных логических элементов. Основными достоинствами этих интегральных микросхем являются малые габариты и вес, низкое энергопотребление, высокая надежность и помехоустойчивость. Интегральные логические микросхемы выпускаются в виде серий, содержащих от единиц до десятков логических элементов, составляющих функционально полный базис. Отличительными признаками элементов, принадлежащих к одной серии, является единство конструктивного исполнения, согласование входных и выходных характеристик, одинаковые требования к источникам питающих напряжений.

В настоящее время отечественной промышленностью выпускается множество серий цифровых интегральных микросхем. Типичным представителем цифровых интегральных микросхем является серия К155. Интегральные микросхемы серии К155 являются потенциальными транзистор-транзисторными схемами. В состав серии входят логические элементы, реализующие логические функции И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ и др. Некоторые из этих элементов входят в состав серии в виде нескольких модификаций, отличающихся числом схем в одном корпусе, количеством входов на одну схему и нагрузочными характеристиками. Помимо указанных логических элементов в состав серии входят расширители входов, элементы памяти и более сложные цифровые устройства [2]. Элементы И-НЕ, входящие в состав серии, имеют условные обозначения ЛА, перед которыми указывается номер серии, а после - номер модификации, например: К155ЛА1, К155ЛА2 и др. В основу всех модификаций элемента И-НЕ положена одна и та же схема со сложным инвертором.

На рис. 2.2,а приведена принципиальная электрическая схема элемента К155ЛА1. На рис.2.2,б показано условное графическое обозначение этого элемента. Каждый элемент содержит две одинаковые трехвходовые логические схемы И-НЕ, имеющие два дополнительных вывода, обеспечивающих подключение схем-расширителей. Логическая схема включает микроэмиттерный транзистор V1 который вместе с резистором R1, образует логическую схему И. Транзисторы V2, V3, V4, V5 и резисторы R2, R3, R4, образуют схему сложного инвертора.

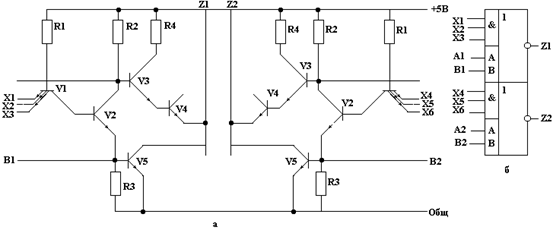
Рис. 2.2

Рассмотрим работу схемы.

Если напряжение на одном из входов схемы не превышает 0,8 В (т.е. на один из входов схемы подан низкий потенциал), то весь ток, текущий через резистор R1, ответвляется на входную цепь схемы. При этом напряжение на базе транзистора V2 составляет несколько десятков милливольт, (т.е. оно равно сумме падений напряжений на переходе коллектор-эмиттер выходного транзистора предыдущего каскада). Поэтому транзисторы V2 и V5 закрыты, а транзистор V3 открыт. Выходное напряжение схемы в этом случае близко к напряжению питания (³2,3 В).

Если на все входы многоэмиттерного транзистора V1 подан высокий потенциал (³1,7 В), то ток, протекающий через резистор R1, ответвляется через базу транзистора V2. Поэтому транзисторы V2 и V5 открыты, а транзистор V3 закрыт, так как напряжение между коллекторами транзисторов V2 и V5 оказывается ниже, чем суммарный порог отпирания транзисторов V3 и V4. Транзистор V4 включен в схему в качестве смещающегося диода. В этом случае через коллекторно-эмиттерный переход транзистора протекают только входные токи схем нагрузок.

Основное назначение транзистора V4 состоит в надежном запирании транзистора V3 при насыщенном состоянии транзисторов V2, V5. Это позволяет уменьшить мощность, потребляемую схемой в этом режиме, а также снизить требования к коэффициенту усиления транзистора V5.

Одна из важных особенностей схемы заключается в том, что при переключении схемы во время переходного процесса оказываются одновременно открытыми транзисторы V2, V3, V4, V5. Это приводит к увеличению тока в цепи питания и потребляемой мощности в момент переключения. Поэтому логические устройства, построенные на этих элементах, в статическом состоянии потребляют меньшую мощность, чем при переключении.

С помощью рассмотренного элемента могут быть реализованы логические функции типа

,

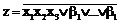где b_i - конъюнкция, реализуемая схемой расширителя, при подключении его к основной схеме;

l - число подключенных расширителей.

При включении рассматриваемых элементов в общую схему на свободные информационные входы должен быть подан высокий уровень напряжения.

Элементы-расширители имеют условное обозначение ЛП и самостоятельно логическую функцию не реализуют. Элементы-расширители строятся на базе многоэмиттерного транзистора и при подключении ко входам А, В основных элементов реализуют конъюнкции входных сигналов.

Следует отметить, что кроме интегральных микросхем, возможна реализация логических функций и цифровых устройств в целом на других элементах автоматики: реле, оптронах, пневматических и т.д., образующих функционально полный базис.

ВЫВОДЫ К ГЛАВЕ 2

1. Базовыми понятиями математического аппарата, используемых в задачах анализа и синтеза ЦА, являются понятия логической переменной и логической функции. Наибольшее распространение не практике получили двоичные логические переменные и функции.

2. Наибольшей наглядностью среди всех способов задания логических функций обладает табличный способ, наибольшей компактностью - числовой и аналитический способы. Наиболее удобен при решении задач преобразования логических функций аналитический способ их задания.

3. Любая сложная логическая функция трех и более переменных может быть получена путем суперпозиции (последовательной подстановки) элементарных логических функций. Среди всех элементарных логических функций только две - И-НЕ и ИЛИ-НЕ - позволяют построить любую сложную логическую функцию без использования других функций.

4. Для того чтобы построить цифровое устройство любой сложности, необходимо иметь набор логических элементов (интегральных микросхем),образующих функционально полный базис.

КОНТРОЛЬНЫЕ ВОПРОСЫ К ГЛАВЕ 2

1. Какая функция называется двоичной логической функцией?

2. Какие типы наборов переменных имеет логическая функция и каково их суммарное число?

3. Сколько логических функций существует для трех логических переменных? Приведите пример вырожденной логической функции трех переменных.

4. Что можно сказать о полностью определенных логических функциях трех переменных f₁ и f₂, заданных таблицами 2.6 и 2.7?

Таблица 2.6

Таблица соответствия логической функции f₁(x)

x3	x2	x1	f1(x)

Таблица 2.7

Таблица соответствия логической функции f₂(x)

x3	x2	x1	f2(x)

5. Запишите в числовом виде логическую функцию z(x), заданную таблицей 2.8.

Таблица 2.8

Двухходовая таблица соответствия логической функции z(x)

x1x2	x3x4
				-
		-
		-	-

Z(x)

6. В чем состоит практическое значение теоремы Поста-Яблонского?

7. Каким образом на практике реализуются элементарные логические функции одной переменной?

8. Определите значение выходного сигнала z₁ логического элемента, показанного на рис. 2.2,б, если x₁=x₂=1, x₃=0 а с помощью расширителя (входы А и В) реализуется конъюнкция b₁=1.

ЛИТЕРАТУРА К ГЛАВЕ 2

2.1. Яблонский С. В. Введение в дискретную математику. - М.: Наука, 1979.

2.2. Корнейчук В. И., Тарасенко В.П., Мишинский Ю. Н. Вычислительные устройства на микросхемах.- Киев: Техника, 1986.

2.3. Дискретные устройства АСУ. / Под ред. Тимонькина Г. Н., Харченко В. С. - Мо СССР, 1990.

2.4. Применение интегральных микросхем в электронной вычислительной технике: Справ./Под ред. Б. Н. Файзулаева, Б.В. Тарабрина. - М.: Радио и связь, 1986.

ГЛАВА 3

ПРЕОБРАЗОВАНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ