Элементарные логические функции
Как указывалось ранее, число различных логических функций очень быстро растет с увеличением числа переменных, и изучить их все невозможно. Однако любую логическую функцию, зависящую от n переменных (n>2), можно выразить через функции, зависящие от одной или двух переменных. Эти функции называют элементарными логическими функциями.
Рассмотрим эти функции.
При n=0 имеются две различных функции: f0=0 и f1=1. Функция f0=0 называется константой 0, а функция f1=1 называется константой 1.
При n=1 имеются четыре логические функции (таблица 2.4).
Таблица 2.4
Элементарные логические функции, зависящие от одной переменной
| fi | x | Задание функции | Название функции | |
| формулой | ||||
| f0 | f0(x)º0 | Константа 0 | ||
| f1 | f1(x)=`x | Инверсия | ||
| f2 | f2(x)=x | Повторения | ||
| f3 | f3(x)=1 | Констант 1 |
Функции f0(x) и f3(x) фактически не зависят от x:
f0(x)º0; f3(x)º1,
т.е. совпадают с функциями нуля переменных.
Значение функции f1(x) совпадает со значением переменной:
f1(x)=x
Это функция повторения.
Значение функции f2(x) противоположно (инверсно) значению переменной x:
f2(x) = 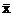 .
.
Функцию f2(x) называют функцией отрицания (инверсией, функцией НЕ). Отметим, что для каждой функции одной переменной существует инверсная ей функция:
f0(x) =`f3(x) ; f3(x) =`f0(x);
f1(x) =`f2(x); f2(x) =`f1(x);
Таблица 2.5
Элементарные логические функции, зависящие от двух переменных
| Набор | Задание функции | Название функции | |||||
| x1 | формулой | ||||||
| x2 | |||||||
| f0 | f0(x)º0 | Константа 0 | |||||
| f1 | f1(x)=x1 ¯x2 | Функция Пирса [или-не] | |||||
| f2 | f2(x)= x1 x2 | Запрет x2 | |||||
| f3 | f3(x)=`x2 | Отрицание x2 | |||||
| f4 | f4(x)= x2 x1 | Запрет x1 | |||||
| f5 | f5(x)=`x1 | Отрицание x1 | |||||
| f6 | f6(x)= x1 Åx2 | Сложение по модулю 2 | |||||
| f7 | f7(x)= x1 / x2 | Функция Шефера[и-не] | |||||
| f8 | f8(x)= x1 x2 | Конъюнкция [и] | |||||
| f9 | f9(x)=x1 ~x2 | Эквивалентность | |||||
| f10 | f10(x)= x1 | Повторение x1 | |||||
| f11 | f11(x)=x2®x1 | Импликация x2 в x1 | |||||
| f12 | f12(x)=x2 | Повторение x2 | |||||
| f13 | f13(x)=x1 ®x2 | Импликация x1 в x2 | |||||
| f14 | f14(x)= x1 Úx2 | Дизъюнкция [или] | |||||
| f15 | f15(x)º1 | Константа 1 | |||||
Логические функции двух переменных приведены в таблице 2.5. Очевидно, что функции
f0(x) = 0; f3(x) =`x2 ; f5(x) =`x1 ;
f10(x)=x1; f12(x)=x2; f15(x)=1
являются элементарными функциями, зависящими от одной переменной. Это вырожденные функции. Остальные десять функций зависят от двух переменных. Функция f8(x1, x2), принимающая значение 1 на наборе 11, а на остальных наборах равная 0, носит название конъюнкции x1 и x2 (логическая функция И). Для ее обозначения будем применять точку или вообще опускать всякий знак (символ) между переменными x1 и x2, т.е.
f8(x1, x2)= x1x2.
Функция f14(x1, x2), принимающая значение 1, когда хотя бы одна из переменных равна единице, носит название дизъюнкции x1 и х2 (логическая функция ИЛИ). Для ее обозначения будем применять символ “Ú” между переменными х1 и х2 т.е.
f14(x1x2)= x1Ú x2.
Функция f1(x1, x2), принимающая значение 1на наборе 00, а на остальных наборах равная 0, носит название функции Пирса или функции ИЛИ-НЕ. Для ее обозначения применяется символ ¯ между переменными х1 и х2 т.е.
f1(x1, x2)= x1 ¯ x2.
Функция f7(x1, x2), принимающая значение 0 на наборе 11, а на остальных наборах равная 1, носит название функции Шеффера, или функции И-НЕ. Для ее обозначения применяется символ / между переменными х1 и х2 т.е.
f7(x1, x2)= x1 / x2.
Функция f9(x1, x2), принимающая значение 1только тогда, когда значения х1 и х2 совпадают, носит название функции эквивалентности. Для ее обозначения используется символ ~ между переменными х1 и х2 т.е.
f9(x1, x2)= x1 ~ x2.
Функция f6(x1, x2), принимающая значение 1только тогда, когда значения х1 и х2 противоположны, носит название функции сложения по модулю два (неэквивалентности, неравнозначности). Для ее обозначения используется символ Å между переменными х1 и х2 т.е.
f6(x1, x2)= x1 Å x2.
Функция f11(x1, x2) и f13(x1, x2) принимающие значение 0 только на наборах 01 или 10 соответственно, а на остальных наборах равные 1, носят название функции импликации х2 в х1 или х1 и х2. Для обозначения этих функций применяется символ “®”между переменными х2 и х1 или х1 и х2 т.е.
f11(x1, x2)= x2® x1;
f13(x1, x2)= x1® x2.
Функция f2(x1, x2) и f4(x1, x2) принимающие значения 1 только на наборах 10 или 01 соответственно, а на остальных наборах равные нулю, носят название функций запрета х2 или х1 и записываются следующим образом:
f2(x1, x2)= x1 x2;
f4(x1, x2)= x2 x1.
Значение рассмотренных функций состоит в том, что из них может быть построена произвольная логическая функция, зависящая более чем от двух переменных. Логические функции, зависящие более чем от двух переменных, называются сложными логическими функциями.
