Математические основы теории цифровых автоматов

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ЦИФРОВЫХ АВТОМАТОВ

ГЛАВА 1

Общие сведения о цифровых автоматах

Понятие о цифровом автомате

Автомат - это устройство, выполняющее некоторый процесс без непосредственного участия человека. Слово автомат происходит от греческого 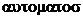-самодействующий.

Цифровой автомат (ЦА) - это математическая модель реального (технического) устройства, служащего для преобразования цифровой информации.

В общем случае ЦА имеет n входов x₁, x₂, ..., x_nи m выходов z₁, z₂, ...,z_m (рис.1.1,а), каждый из которых может принимать некоторое конечное число дискретных значений. Число входов и выходов цифрового автомата конечно. Входы x₁, x₂, ..., x_n образуют множество входов цифрового автомата:

X={x₁, x₂, ...,x_n}.

Выходы z₁, z₂, ...,z_m образуют множество выходов цифрового автомата:

Z={z₁, z₂, ...,z_m}.

Зависимость между выходными и входными сигналами в цифровом автомате реализуется с помощью соединения элементов, которые принято называть логическими.

В цифровых автоматах могут присутствовать элементы, которые, изменяя свое состояние под действием входных сигналов или порождаемых ими управляющих воздействий, после прекращения действия этих сигналов в исходное состояние не возвращаются.

Вторично изменить свое состояние или вернуться в исходное эти элементы могут после воздействия других входных сигналов или повторного воздействия тех же входных сигналов или сигналов ими порождаемых. Такие элементы принято называть элементами памяти (ЭП) цифрового автомата. Типичными представителями элементов памяти являются широко применяемые на практике тригерные устройства различных типов.

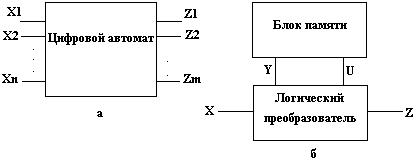
Рис.1.1.

Наличие в цифровом автомате элементов памяти значительно расширяет возможности преобразования информации, при этом могут запоминаться значения входных сигналов, поступающих в предыдущие моменты времени, и использоваться при формировании выходных сигналов.

При решении задач анализа и синтеза цифровых автоматов элементы памяти принято выделять в отдельный блок, который называется блоком памяти или просто памятью цифрового автомата (рис.1.1,б). Часть схемы автомата, не содержащая элементов памяти, называется логическим преобразователем или комбинационным блоком автомата. ЦА, представленный на рис. 1.1,б, получил название канонического автомата или автомата с канонической структурой.

В общем случае блок памяти цифрового автомата может содержать k элементов памяти y₁, y₂, ...,y_k, каждый из которых может принимать некоторое конечное число состояний. Элементы y₁, y₂, ...,y_k образуют множество элементов памяти автомата:

Y={ y₁, y₂, ...,y_k}

Значение переменной y_i будем отождествлять с состоянием обозначаемого этой переменной элемента памяти. Состояние каждого элемента памяти однозначно определяет выходной сигнал, формируемый этим элементом. Поэтому для обозначений сигналов, формируемых элементами памяти, можно использовать те же буквы которые обозначают элементы памяти, а множество Y={ y₁, y₂, ...,y_k } в необходимых случаях будем рассматривать как множество выходов блока памяти автомата.

Логический преобразователь автомата помимо формирования выходных сигналов обеспечивает управление блоком памяти цифрового автомата. Для этого он имеет l выходов управления памятью u₁, u₂, ...,u_l, которые образуют множество выходов управления памятью:

U={u₁, u₂, ...,u_l}.

Выходы логического преобразователя непосредственно соединяются с соответствующими входами блока памяти автомата. Поэтому множество u нередко называют множеством входов управления памятью автомата. В общем случае l 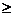k, так как каждый элемент памяти автомата может иметь один или несколько управляющих входов. Так, при построении памяти автомата на RS-триггерах мощность множества u в два раза превышает мощность множества Y, т.е. l=2k. Ввиду простоты технической реализации в настоящее время наибольшее распространение получили цифровые автоматы, сигналы в которых принимают только два возможных значения. При математическом описании таких сигналов, независимо от физической природы, их значения отождествляют с цифрами 0 и 1. В дальнейшем изложении будем рассматривать автоматы, работающие только с двоичными сигналами.

Если каждому входному сигналу автомата присвоить конкретное значение на множестве {0,1}, то полученная совокупность значений входных сигналов будет представлять собой комбинацию значений входных сигналов или входной набор цифрового автомата. В общем виде входной набор цифрового автомата запишется следующим выражением:

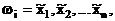
где

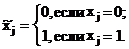
Так как каждый входной сигнал цифрового автомата может принимать одно из двух возможных значений независимо от значений других входов, то максимальное число различных входных наборов определяется как произведение, состоящее из n цифр 2, т.е.

N_вх=2ⁿ .

Таким образом, максимальная мощность множества входных наборов цифрового автомата равна 2ⁿ. Множество входных наборов автомата будем записывать в виде

,

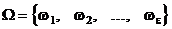где .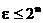

Выходной набор цифрового автомата будем записывать в виде

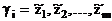
Совокупность выходных наборов образует множество выходных наборов автомата:

,

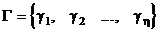где 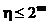- мощность множества выходных наборов цифрового автомата.

Введем также понятие „набор состояний элементов памяти автомата“, или просто „внутреннее состояние памяти“ („внутреннее состояние“) -

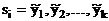
и множество состояний памяти цифрового автомата:

,

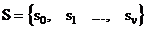где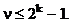

Отличительной особенностью задания этого множества является нумерация состояний памяти, начиная с состояния S₀, которое выделяется специально для обозначения начального состояния памяти автомата. В связи с этим максимальный номер последнего состояния будет равен 2^k-1, а максимальная мощность множества состояний памяти автомата -2^k

Цифровые автоматы в зависимости от количества состояний памяти делятся на автоматы с одним внутренним состоянием, у которых элементы памяти отсутствуют, и автоматы с двумя и более внутренними состояниями, содержащие один и более элементов памяти.

Цифровые автоматы с двумя и более внутренними состояниями называют цифровыми автоматами с памятью или последовательностями машин. Принципиальным отличительным признаком цифровых автоматов с памятью является то, что значения выходных сигналов (наборы значений выходных сигналов) у них определяются не только значениями входных сигналов (входными наборами), поступившими в этот момент времени, но и их предыдущими значениями, а также порядком их поступления на входы автомата.

Если элементы памяти в схеме автомата отсутствуют, считается, что такой автомат имеет одно внутреннее состояние, которое полностью определяется составом и схемой соединения его элементов. Цифровые автоматы этого типа называют цифровыми автоматами без памяти, комбинационными автоматами или логическими преобразователями. Работа таких автоматов состоит в том, что они сопоставляют каждому входному набору некоторый выходной набор, значение которого полностью определяется значениями входных сигналов, действующих в данный момент времени, и никак не зависит от предшествующих значений состояний входов. Таким образом, цифровой автомат без памяти можно рассматривать как частный случай цифрового автомата с памятью, у которого число внутренних состояний сведено к одному, а элементы памяти отсутствуют. С другой стороны, цифровой автомат с памятью представляет собой совокупность цифрового автомата без памяти и элементов памяти, объединенных в блок памяти автомата. В общем случае выходные сигналы автомата определяются как входными сигналами, так и состояниями элементов памяти автомата, которые в комплексе характеризуют состояние автомата. Для записи состояний автомата будем использовать следующую запись:

,

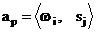которая обозначает, что состояние цифрового автомата a_p характеризуется входным набором 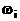и состоянием памяти s_j.

Совокупность состояний a_p образует множество состояний автомата

A={a₁, a₂, ...,a_µ}.

Если допустить, что при каждом входном наборе автомат может находиться в любом из внутренних состояний, то максимальное число состояний цифрового автомата определяется как произведение максимального числа входных наборов на максимальное число его состояний памяти:

N_сост =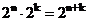

Полученное число определяет максимальную мощность множества А и, следовательно, для реальных автоматов 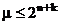. Число состояний µ быстро возрастает с увеличением сложности автомата, числа входов и элементов памяти.

Общая структурная схема ЦА

Выше были рассмотрены варианты схемы ЦА с канонической структурой без учета особенностей элементной базы и возможностей изменения выполняемых функций.

Структурная схема автомата в общем случае определяется совокупностью реализуемых функций. Вместе с тем между реализуемыми функциями и структурной схемой не существует взаимно однозначного соответствия: один и тот же набор функций может быть реализован различными совокупностями функциональных элементов (ФЭ), объединенных в ЦА. Эти элементы соответствуют совокупности операций алгоритма реализации заданных функций.

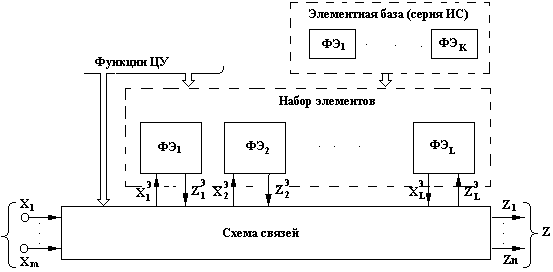
Рис.1.5

Общая структура ЦА с входами Х₁, ...,Х_m, выходами Z₁, ...,Z_n и совокупностью ФЭ₄, ...,ФЭ_L показана на рис. 1.5.

У каждого ФЭ_i=(i= 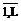) входы Х_i^э связаны с одним или несколькими входами Х₁, ...,Х_m устройства или выходами Z₁^э, ...,Z_L^э других элементов посредством схемы связей. Выходы Z_i^э элемента связаны со входами одного или нескольких функциональных элементов или выходами Z₁, ...,Z_n устройства. Элемент ФЭ_i выполняет операцию F_i^э из множества

F={F₁,F₂, ...,F_k}; Z_i^э=F_i^э(X_i^э).

Множества операций F может, например, включать набор арифметических операций: сложение, вычитание, умножение и деление двух кодов, составляющих Х_i^э.

Таким образом, наборы входных сигналов (выходные коды) Х₁, ..., Х_m, проходя через последовательность функциональных элементов ФЭ₁, ..., ФЭ_L преобразуются в набор выходных сигналов ЦА Z₁, ...,Z_n.

Каждый функциональный элемент может иметь сложную структуру из более простых элементов и т.д. В реальных, даже самых сложных цифровых устройствах и системах число уровней разбиения не превышает 6-8.

Простейшими функциональными элементами являются логические вентили, выполняющие элементарные функции, и элементы памяти (ЭП), предназначенные для хранения значений сигналов.

На нижнем уровне структурного разбиения ЦА представляется структурной схемой, включающей набор элементов из используемой элементной базы.

Элементная база ЦА

Элементы ЦА могут быть оптическими, магнитными, электромагнитными (контактными), электронными (бесконтактными) и др. В настоящее время наиболее широкое распространение получили электронные полупроводниковые элементы в интегральном исполнении - цифровые интегральные схемы (ИС). Они представляют собой набор базовых элементов - вентилей, объединенных соединительными проводниками на полупроводниковом кристалле, который размещается в одном из стандартных корпусов.

Электронные полупроводниковые элементы, выполненные в виде ИС, обладают такими преимуществами, как малые размеры и потребляемая мощность, повышенная надежность, удобство и высокая плотность монтажа. Высокая технологичность позволяет выпускать ИС большими сериями, что обуславливает их сравнительно малую стоимость.

ИС обладают рядом особенностей.

1. По мере совершенствования технологии изготовления уменьшаются линейные размеры компонентов вентилей (транзисторов, диодов и др.) и ширина соединительных проводников. Современной микроэлектроникой достигнуты линейные размеры компонентов 1-3 мкм, что позволяет на кристалле площадью 20-30 мм² размещать до 10 компонентов (до 10⁵ вентилей). Число вентилей N на кристалле определяет степень интеграции ИС. Уменьшение линейных размеров компонентов в 4 раза приводит к увеличению степени интеграции в 10 раз, а быстродействия - в 4 раза, потребляемая же каждым вентилем мощность уменьшается при этом в 16 раз. Ежегодно степень интеграции ИС увеличивается в 2 раза, быстродействие в 1,5 раза, в то время как стоимость, надежность и потребляемая мощность изменяется значительно медленнее. Следовательно, увеличение степени интеграции ИС является эффективным способом улучшения весогабаритных параметров, экономичности и надежности ЦА на их основе.

В будущем на кристалле СБИС ожидается размещение до 10¹⁰ компонентов.

По степени интеграции ИС делятся на:

- ИС малой степени интеграции (МИС) с N<10;

- ИС средней степени интеграции (СИС) с 10£N<100;

- ИС большой степени интеграции (БИС) с 100£N<100;

- ИС сверхбольшой степени интеграции (СБИС) с N>1000.

2. Стандартные корпуса ИС малогабаритные и имеют по 14,16,18,24,28,40,42,48 или 64 вывода. Корпуса с большим числом выводов в настоящее время получили для ИС, используемых в специальных устройствах. Существующее ограничение на число входов и выходов БИС затрудняет доступ к внутренним элементам и определенным образом влияет на выбор структуры БИС и СБИС.

3. Соединительные проводники сложной схемы связей элементов занимают на кристалле значительную площадь и снижают степень интеграции ИС. Наибольшей степенью интеграции обладают БИС и СБИС с регулярной матричной схемой связей.

4. Стоимость проектирования БИС и СБИС очень велика, поэтому производство единичных заказных ИС оправдывается в исключительных случаях. Экономически целесообразен лишь массовый выпуск ИС, обеспечивающий их малую стоимость. По этой причине номенклатура ИС ограничена. Микроэлектронной промышленностью выпускается ряд серий ИС, каждая из которых включает от единиц до нескольких десятков ИС различной степени интеграции, выполненных по единой технологии (р-МОП, п-МОП, КМОП, ТТЛ, ЭСЛ, И²Л и др.) и совместимых между собой. Элементная база ЦА, как правило, состоит из ИС одной серии.

5. Введение элементов настройки резко расширяет функциональные возможности ИС. Такие ИС настраиваются на выполнение требуемых функций:

а) на последней стадии изготовления (полузаказные ИС);

б) однократно после изготовления ИС;

в) многократно после изготовления ИС.

Использование программируемых ИС позволяет разрешить противоречие между ограниченной номенклатурой ИС и необходимостью реализации с их помощью самых разнообразных функций.

6. Устойчивость ИС к воздействию внешних факторов (температуры, влажности, электрических и магнитных полей) достаточно высока. Это позволяет строить на их основе ЦА, предназначенные для использования в самых различных условиях эксплуатации.

В недавнем прошлом 10⁵¸10⁶ элементов являлись пределом возможностей технической реализации цифровых устройств и систем. В настоящее время эти элементы могут быть размещены в одной СБИС на кристалле площадью около 1см².

С точки зрения удобства наладки, надежности и психологической обозримости цифровая система могла бы содержать 200¸400 тис. БИС или квадратных сантиметров площади кристаллов.

Таблица соответствия полностью и неполностью определенных логических функций z(x) и u(x)

w10	x3	x2	x1	z(x)	u(x)
					~
					~
					~

При задании неполностью определенных функций таблицами соответствия значения функции на условных наборах будем обозначать “-“ или “~” как показано в таблице соответствия 2.2 для логической функции u(x).

Рассмотренный способ задания функций приемлем для функций небольшого числа переменных, так как с увеличением числа переменных (n) количество наборов увеличится как 2ⁿ и таблица соответствия получается громоздкой.

Более компактным табличным способом задания логических функций является использование двухвходовых таблиц соответствия. Для построения такой таблицы переменные, от которых зависит логическая функция, разделяются на две примерно равные группы. Для образования групп переменных определяются всевозможные наборы их значений. Строки таблицы в произвольном порядке обозначаются наборами переменных первой группы, а столбцы таблицы - наборами переменных второй группы. Каждая клетка такой таблицы соответствует одному набору значений переменных, от которых зависит функция. В каждой клетке таблицы проставляется значение функции на соответствующем ей наборе значений переменных. Количество клеток такой таблицы соответствует числу всевозможных наборов значений переменных. Примером двухуровневой таблицы является таблица 2.3 в которой задана неполностью определенная логическая функция трех переменных u(x).

Таблица 2.3

Двухвходовая таблица соответствия для логической функции u(x)

x3	x3 x1
				~
	~	~

u(x)

Удобным способом задания логических функций является использование номеров единичных, нулевых или неопределенных наборов. Для этой цели любой набор будем рассматривать как представление целого неотрицательного числа в двоичной системе счисления, которая также оперирует с цифрами “0” и “1”. Целое число в двоичной системе счисления можно представить эквивалентным ему числом в десятичной или восьмеричной системах счисления. Эти числа будем называть номерами наборов в двоичной, восьмеричной или десятичной системах счисления, что позволит записывать в компактной форме наборы значений переменных логической функции. При этом будем полагать, что в двоичном числе младший разряд расположен справа. Например, набор 10011 может быть представлен десятичным числом

1×2⁴+0×2³+0×2²+1×2¹+1×2⁰=19,

а набор 1110 - числом

1×2³+1×2²+1×2¹+0×2=14.

Для представления набора (двоичного числа) в восьмеричной системе счисления необходимо его разделить на триады, начиная с младшего разряда, и каждую триаду записать цифрой в восьмеричной системе счисления. Например, набор 110011 может быть представлен восьмеричным числом 63, так как 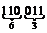® 63.

При разделении двоичного набора на триады крайняя левая триада может оказаться неполной. В этом случае значения старших недостающих разрядов двоичного набора принимаются равными нулю. Например, двоичному набору 1101110 соответствует восьмеричное числоь156, так как 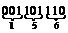® 156.

Удобство использования восьмеричной системы счисления состоит в том, что при записи двоичного набора в этой системе счисления сохраняется взаимооднозначное соответствие между разрядами восьмеричного числа и триадами двоичного набора (двоичного числа). Это позволяет легко переходить от задания двоичного набора значений переменных логических функций к восьмеричному числу и наоборот.

Для однозначного задания двоичного набора значений переменных необходимо указать его номер, систему счисления, в которой задан номер, порядок расположения переменных и размерность, т.е. количество переменных логических функций. Так, например, десятичному числу 25 соответствует набор 11001 при размерности 5 или набор 0011001 при размерности 7.

Условимся при задании логической функции номерами единичные наборы записывать в квадратных скобках, нулевые в круглых скобках, а неопределенные - в фигурных скобках. При задании логической функции номерами единичных и нулевых наборов первыми после квадратной скобки указываются номера единичных наборов, а затем в круглых скобках - номера нулевых наборов. За последней скобкой указывается основание системы счисления. Например логическая функция z(x) (таблица 2.2) может быть задана номерами единичных и нулевых наборов в виде

z(x₃, x_2, x₁)=[3, 5, 6, 7 (0, 1, 2, 4)]₁₀.

При задании неполностью определенной логической функции номерами единичных и неопределенных наборов, а затем в фигурных скобках - номера неопределенных наборов. Например, функция u(x) (табл.2.3) может быть задана выражением

u(x₃, x_2, x₁)=[1, 5, {3, 4,6}]₁₀.

При задании логической функции номерами нулевых и неопределенных наборов первыми после круглой скобки записываются номера нулевых наборов, а затем в фигурных скобках -номера неопределенных наборов. Например, функция, рассмотренная в предыдущем примере, может быть задана выражением

u(x₃, x_2, x₁)=[0, 2, 7 (3, 4, 6)]₁₀.

Необходимо отметить, что при таком способе задания, в зависимости от указанного порядка переменных, одними и теми же совокупностями номеров наборов могут быть заданы различные логический функции.

Произвольная логическая функция может быть задана в виде аналитического выражения (формулы), представляющего совокупность переменных, объединяемых определенными логическими операциями, которые будут введены в следующих параграфах.

Z(x)

6. В чем состоит практическое значение теоремы Поста-Яблонского?

7. Каким образом на практике реализуются элементарные логические функции одной переменной?

8. Определите значение выходного сигнала z₁ логического элемента, показанного на рис. 2.2,б, если x₁=x₂=1, x₃=0 а с помощью расширителя (входы А и В) реализуется конъюнкция b₁=1.

ЛИТЕРАТУРА К ГЛАВЕ 2

2.1. Яблонский С. В. Введение в дискретную математику. - М.: Наука, 1979.

2.2. Корнейчук В. И., Тарасенко В.П., Мишинский Ю. Н. Вычислительные устройства на микросхемах.- Киев: Техника, 1986.

2.3. Дискретные устройства АСУ. / Под ред. Тимонькина Г. Н., Харченко В. С. - Мо СССР, 1990.

2.4. Применение интегральных микросхем в электронной вычислительной технике: Справ./Под ред. Б. Н. Файзулаева, Б.В. Тарабрина. - М.: Радио и связь, 1986.

ГЛАВА 3

ПРЕОБРАЗОВАНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ

Для каждой строки таблицы, в которой функция равна единице, составляется элементарная конъюнкция всех переменных. При этом в конъюнкцию входит сама переменная, если ее значение равно единице, или отрицание если ее значение равно нулю. Полученные элементарные конъюнкции объединяются знаком дизъюнкции.

Пример 3.3.Для логической функции z(х), заданной таблицей соответствия 2.2, определим совершенную дизъюнктивную нормальную форму.

Для четвертой строки таблицы, которая соответствует единичному набору функции 011, найдем конституенту единицы `х₃х₂х₁.

Выполнив логические операции для шестой, седьмой и восьмой строк, определим искомую СДНФ функции:

.

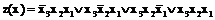Таким образом, СДНФ логических функций получается путем использования операций и аксиом алгебры логики.

Для каждой строки таблицы соответствия, в которой функция равна нулю, составляется элементарная дизъюнкция всех переменных. При этом в дизъюнкцию входит сама переменная, если ее значение равно нулю, или отрицание, если ее значение равно единице. Полученные элементарные дизъюнкции объединяются знаком конъюнкции.

Пример 3.4.Для логической функции z(x), заданной таблицей соответствия 2.2, определим совершенную конъюнктивную форму.

Для первой строки таблицы, которая соответствует нулевому набору функции 000, находим конституенту нуля 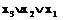. Выполнив аналогичные операции для второй, третьей и пятой строк, определим искомую совершенную КНФ функции:

.

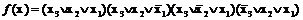Необходимо отметить, что для функций, число единичных наборов которых превышает число нулевых наборов, более компактной является их запись в виде СКНФ и наоборот.

Для получения сокращенной ДНФ логической функции по карте Карно необходимо найти все правильные контуры, охватывающие единичные клетки, выписать соответствующие им простые импликанты и объединить их знаком дизъюнкции.

При минимизации неполностью определенных логических функций контуры могут охватывать клетки, соответствующие условным наборам, однако каждый выделенный максимальный контур должен охватывать хотя бы одну клетку, содержащую единицу.

Для получения тупиковой ДНФ логической функции по карте Карно необходимо найти такую совокупность максимальных правильных контуров, у которых каждый контур охватывал хотя бы одну клетку, содержащую единицу, и не охваченную другими контурами, а совокупность контуров была полной, т.е. охватывала бы все единичные клетки карты Карно. Кроме того, необходимо выписать соответствующие им простые импликанты и объединить их знаком дизъюнкции.

При определении тупиковых ДНФ логических функций по картам Карно прежде всего должны быть определены максимальные правильные контуры, соответствующие существенным простым импликантам, составляющим ядро логической функции. Отличительным признаком такого контура является вхождение в него хотя бы одной единичной клетки, которая может быть охвачена только этим контуром. Так, из рис. 3.3, а видно, что существенным контуром представленной на карте Карно функции является контур, охватывающий в единственном числе единичную клетку, соответствующую набору 0100. Указанный контур соответствует простой импликанте ядра логической функции и должен входить во все тупиковые формы.

После выбора контуров, соответствующих ядру логической функции, для покрытия оставшихся единичных клеток вводятся дополнительные максимальные контуры до тех пор, пока совокупность контуров не станет полной. При этом необходимо соблюдать осторожность, проверяя после введения каждого нового контура выполнение правила, требующего, чтобы каждый из выделенных контуров охватывал хотя бы одну единичную клетку, не охваченную другими контурами.

Пример 3.6.Определим тупиковые ДНФ логической функции, заданной на карте Карно (рис. 3.3, а). На рис. 3.3,б,в показаны карты Карно, на которых выделены совокупности контуров, соответствующие двум различным тупиковым формам логической функции. Найдем соответствующие выделенным контурам простые импликанты и запишем две тупиковые формы данной логической функции:

= ;

= .

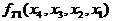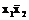
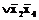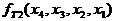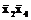
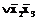
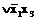Тупиковая форма 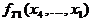содержит меньшее число переменных и является минимальной дизъюнктивной нормальной формой рассматриваемой логической функции.

x4x3	x2x1
			~
	~

x3x4	x2x1
			~
	~

x4x3	x2x1
			~
	~

а б в

Рис. 3.3 Полные совокупности максимальных правильных контуров, соответствующих сокращенной (а), минимальной (б) и тупиковой (в) формам логической функции

С помощью карт Карно могут быть получены сокращенные и тупиковые конъюнктивные нормальные формы логических функций. Методика получения сокращенных и тупиковых КНФ полностью аналогична получению соответствующих дизъюнктивных форм и базируется на следующих основных положениях.

Правильный контур карты Карно, охватывающий одну клетку или группу клеток, соответствующих нулевым или нулевым и неопределенным значениям функции, и имеющий максимальный размер, соответствует простой имплиценте логической функции.

Правило записи имплицент логической функции аналогично определению конституент нуля логической функции по таблице соответствия или записи совершенной конъюнктивной формы функции. В элементарную дизъюнкцию, соответствующую имплиценте логической функции, включается переменная, если ее значения в клетках контура постоянны и равны нулю, и отрицание переменной , если ее значения постоянны и равны единице. Например, на рис. 3.4, а показаны двухклеточный и четырехклеточный максимальные правильные контуры, охватывающие нулевые и неопределенные клетки карты Карно.

x4x3	x2x1
				~
		~	~
		~
		~

x3x4	x2x1
			~
				~
			~
	~

а б

Рис. 3.4. Совокупности максимальных правильных контуров, соответствующие

простым имплицентам 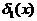, 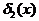(а) и функции 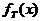(б)

Соответствующие им простые импликанты имеют вид

;

.

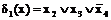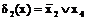Сформулируем правило получения сокращенной и тупиковой конъюнктивных нормальной форм.

Для получения сокращенной КНФ логической функции по карте Карно необходимо найти все максимальные правильные контуры, охватывающие нулевые и неопределенные клетки, выписать соответствующие им простые имплиценты и объединить их знаком конъюнкции. При этом каждый из выделенных максимальных контуров должен охватывать хотя бы одну нулевую клетку.

Для получения тупиковой КНФ логической функции по карте Карно необходимо найти такую совокупность максимальных правильных контуров, у которых каждый контур этой совокупности охватывал хотя бы одну клетку, содержащую нуль, и не охваченную другими контурами, а совокупность контуров была полной, выписать соответствующие им простые имплиценты и объединить их знаком конъюнкции.

Пример 3.7.Определим тупиковую КНФ логической функции, заданной на карте Карно (рис. 3.1, б).

На рисунке показана карта Карно, на которой выделена совокупность контуров, соответствующая тупиковой КНФ логической функции. Определив соответствующие контурам имплиценты и объединив их знаком конъюнкции, получим

= .

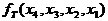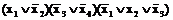Используя другие комбинации контуров для рассматриваемой логической функции, можно найти еще три тупиковые конъюнктивные нормальные формы.

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ЦИФРОВЫХ АВТОМАТОВ

ГЛАВА 1