Логические Функции. Алгебра логики

Для грамотного применения логических функций вспомним некоторые основные положения алгебры логики.В алгебре логики объектами изучения являются:высказывания, логические операции илогические выражения.

Высказывание–это может быть предложение в любой форме (повествовательное, условие и т.п.), относительно которого имеет смысл говоритьне об его содержании, а только то, что оно истинно(имеет значение ИСТИНА, 1) или ложно (ЛОЖЬ, 0). В алгебре логики определены три основные логические операции над высказываниями: логическое сложение (ИЛИ, дизъюнкция), логическое умножение (И, конъюнкция)и логическое отрицание (НЕ, инверсия).Логические операции – это действия над высказываниями, которые являются их аргументами.Определены законы (аксиомы) алгебры логики для выполнения этих операций. Все операции алгебры определяются таблицами истинности, которые определяют результат для всех возможных логических значений исходных высказываний. Если число высказываний в логической операции N, то таблица истинности будет содержать 2^Nразличных комбинаций (строк) возможных значений аргументов.

Действия, которые выполняются над высказываниями, записываются в виделогических выражений. Логические выражения могут быть простыми и сложными.

Простое логическое выражение состоит из одного высказывания и не содержит логических операций. Сложное логическое выражениесодержит логические операции с высказываниями в качестве аргументов.

Операция НЕ(условное обозначение ) применяется к одному аргументу, в качестве которого может быть простое и сложное логическое выражение. Результат операции определяется таблицей истинности (рис.1.1, а).

ОперацииИЛИ (условное обозначение 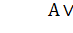И (условное обозначение применяются к двум и более высказываниям. Результаты операции ИЛИиИопределяются таблицами истинности (рис. 1.1,б, в).

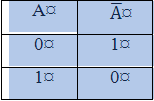
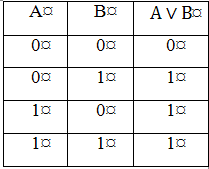
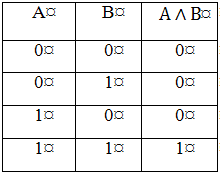
а) б) с)

Рис. 1.1. Таблицы истинности для логических операций НЕ (а), ИЛИ (б), И (с)

Законы (аксиомы) алгебры логики позволяют преобразовать сложные логические выражения с целью их упрощения. Некоторые из существующих законов приведены в таблице 1.

	Для операции ИЛИ	Для операцииИ
Ассоциативность (независимость от порядка выполнения однотипных операций)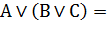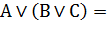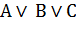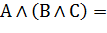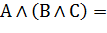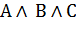
Коммутативность (независимость от перестановки)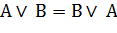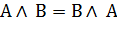
Дистрибутивность(правило раскрытия скобок и вынесения за скобки)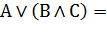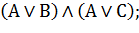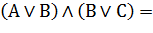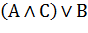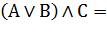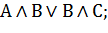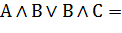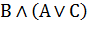
Двойное отрицание	=А
Законы Де Моргана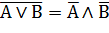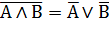
Поглощение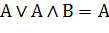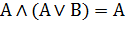
Поглощение отрицания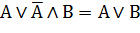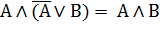
Действия с абсолютно истинными и абсолютно ложными высказываниями	А 1=1 А 0=А	А 1=А А 0=0

С помощью таблиц истинности можно проверить равносильность двух любых сложных высказываний.Для этого следует доказать равенство значений этих высказываний на множестве значений всех простых высказываний, входящих в них. Рассмотрим пример доказательства Закона Де Моргана для операции ИЛИ (табл.2).

Табл.2

А	В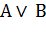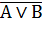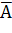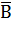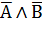

При решении логических задач в электронной таблице объектами, над которыми выполняются действия, являются: логическое условие, логические функции и логические формулы. Логическое условие является аналогом высказывания в алгебре логики. Логические функции являются аналогом логических операторов.Логические формулы используются в MSExcelдлязаписи логических условий (логических выражений).

Логическое условиепредставляет собой величины или выражения одного типа, связанные знаком операции отношений: =(равно), <(меньше), >(больше), <=(не больше), >=(не меньше), <> (не равно). Такие логические условия называются простыми.Такие логические условия могут быть составлены из данных, ссылок и выражений. Например, А1>0, где А1 – это ссылка на ячейку, в которую введено числовое значение; A2>A1, где А1 и А2 ссылки на ячейки с числовыми значениями; ABS(A4)<=B4, где в А4 и В4 ссылки на ячейки с числовыми значениями, ABS(A4)‑выражение; B5*B6<0, где в В5 и В6 введены формулы для вычисления значенияf(x)при x=a (В5) и (В6) при x=bпо формуле f(x)=x³+2x²-3x-1. В ячейку B5 введена формула вида

=A5^3+2*A5^2-3*A5-1,

где в А5 введено численное значение a. Аналогичная формула введена в ячейку В6, в которой используется ссылка на ячейку А6, в которую введено значение b.

Логические функциивычисляют логические выражения и возвращают в качестве результата одно из двух значений: ИСТИНАили ЛОЖЬ, которые могут затем использоваться для выполнения других действий или форматирования. Доступ к логическим функциям открывается из раскрывающегося меню кнопки Логические, находящейся на вкладке ФормулыЛентыа также при выборе категории Логические в диалоговом окне Мастерфункций.Некоторые логические функции (всего 7 логических функций) и описание их назначения приведены в табл. 1.1.

Таблица 1.1.Логические функции и описание их назначения

Функция	Назначение
И (Логическое И)	И(логическое условие1; логическое условие2;…)‑ возвращает значение: ИСТИНА, если все аргументы имеют значение ИСТИНА; ЛОЖЬ, если хотя бы один аргумент имеет значение ЛОЖЬ
ИЛИ (Логическое ИЛИ	ИЛИ(логическоеусловие1; логическоеусловие2;…)‑ возвращает значение: ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ;ИСТИНА, если хотя бы один аргумент имеет значение ИСТИНА.
НЕ (Логическое отрицание)	НЕ(логическоеусловие)‑ возвращает значение ЛОЖЬесли аргумент имеет значение ИСТИНАи наоборот.
ЕСЛИ (Условный выбор)	ЕСЛИ(логическое выражение; значение, если истина; значение, если ложь)‑проверяет на истинность условие в логическом выражении. Если условие выполняется то значением функции будетзначение, если истина, а если условие не выполняется - то значение, если ложь.

Аргументы значение, если истина, и значение, если ложьфункцииЕСЛИ могут содержать константы (числовые или текстовые) и выражения, результаты которых возвращаются в ячейку в качестве значения функции ЕСЛИ.

Принятие решения в формулах

Для принятия решения используется логическая функция ЕСЛИ().Анализ ситуации и выбор (принятие) решения. Во всех описанных ситуациях, требующих принятия решения, за словом «ЕСЛИ» следуетлогическое условие,принимающее значение ИСТИНА или ЛОЖЬ(условие – это аналог высказывания). По смыслу операции сравнения в логическом условии можно однозначно утверждать, что значение такого условия может быть ИСТИНА, если условие выполняется, и ЛОЖЬ‑в противном случае. Результат проверки логического условия (ИСТИНА или ЛОЖЬ) влияет на последующие действия в алгоритме.

Для освоения назначения логических функций, которые используются в электронных таблицах при анализе ситуации и принятии решения (логические задачи), рассмотрим примеры их применения.

Табл. 1.1.

Примеры применения логических функций

№ п/п	Адрес ячейки	Значение	Функция, выражение	Результат	Анализ ситуации
I	Простые логические условия
1.1	А1 B1	3,5	=А1>0	ИСТИНА	Высказывание: значение в ячейке B1 будет ИСТИНА при любых положительных значениях в ячейке А1
1.2	A1 A2 B2	3,5 2,0	=A2>A1	ЛОЖЬ	Высказывание: значение в ячейке B2 будет ИСТИНА при любых значениях в ячейках А2 и А1 таких, что значение в А2 должно быть больше, чем в А1.
1.3	А4 B4 C4	-0,00001 1,00E-5	=ABS(A4)<=B4	ИСТИНА	Высказывание: значение в ячейке C4будет ИСТИНА при любых значениях в ячейке A4 таких, что значение в A4 должно быть не больше по модулю, чем в B4.
1.4	A5 A6 B5 B6 D6	-3 -2,5	-1 3,375 ==B5*B6<0	ИСТИНА	Высказывание: значение в ячейке D6будет ИСТИНА при разных по знаку значениях в ячейкахB5 иB6 и ЛОЖЬ в противном случае.
II	Сложные логические условия
2.1	A1 A2 A3 B3	3,5 2,0 2,5	=И(A3>=A2; A3<A1)	ИСТИНА	Высказывание: значение в ячейке B7будет ИСТИНА при значениях в ячейкеA3, которые принадлежат интервалу [A1,A2) и ЛОЖЬ в противном случае.
2.2	A1 A2 A3 C3	3,5 2,0 2,5	=ИЛИ(A3<A2; A3>=A1)	ЛОЖЬ	Высказывание: значение в ячейке C3будет ИСТИНА при значениях в ячейкеA3, которые не принадлежат интервалу [A1,A2) и ЛОЖЬ в противном случае
2.3	C5 C6 E6	5,75	=И(B5*B6<0;C5*C6>0)	ИСТИНА	Высказывание: значение в ячейке E6:ИСТИНА при разных по знаку значениях в ячейках B5 и B6 «И» одинаковых по знаку значениях в ячейкахС5 иС6; ЛОЖЬ в противном случае.
III	Логическая функция ЕСЛИ для принятия решения
3.1	E2		=ЕСЛИA2>A1;A2; A1)	A2	Выполнить анализ результатов функции ЕСЛИ при других данных в ячейках А1, А2.
3.2	F1 F2 E4	Текст Текст	=ЕСЛИ(ABS(A4)<=C1; “Текст из ячейки F1”; “Текст из ячейки F2”)	Текст из ячейки F1	Выполнить анализ результатов функции ЕСЛИ при других данных в ячейке А4.
3.3	F3   F5   F6	“Имеет ся корень “Корня нет”	=ЕСЛИ(И(В5*В6<0;C5 *C6>0); F3;F5)	Текст из ячейки F3	Выполнить анализ результатов функцииЕСЛИ при других данных в ячейках B5,B6 и C5,C6.