Операции над множествами : объединение, пересечение, вычитание, дополнение, симметрическое вычитание, декартово умножение.

Множество (неопределяемое понятие) – сов-ть предметов, объединенных в одну какую-л группу.

Мн-во В явл-ся подмн-вом мн-ва А, если кажд эл-т мн-ва В явл-ся также эл-ом мн-ва А. Æ считают подм-вом любого мн-ва. Любое мн-во – подмн-во самого себя. (ВÌА).В: «На 4 и 5» А: «с коротк стрижкой».

Пересеченuем мн-в А u В наз мн-во, содержащее те u только те эл-ты, кот прuнадлежат мн-ву А u мн В.

А ÇВ = {х I х Е А и х Е В}.Если изобраз мн-ва А и В с пом кругов Эйлера, то Ç-ем дан мн-в явл заштрих обл.

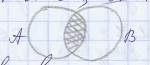в том случ, когда мн-ва А и В не им общих эл-тов, говорят, что их Ç-е пусто: А Ç В = Æ.

А – мн-во четн натур чисел В – мн-во двузн чисел.

Ха­рактеристическое св-во эл-тов мн-ва А-«быть четн натур числом»,В - «быть двузн числом».Т.О, мн-во

А Ç В сост из четн двузн чисел. Полученное мн-во не пусто.Н-р, 24 Î АÇВ, п.ч. число 24 четн и двузн.

А-мн-во всех ромбов, В –прямоуг. АÇВ-квадратов.

Теорема о cв-вах пересечения.

1ºАÇВ=ВÇА (коммутат) 2º(АÇВ)ÇС=АÇ(ВÇС) (асс)

3º АÇА=А (идемпотентность) 4º АÇÆ=Æ

5ºЕсли АÌВ, то АÇВ=А (меньшему из них)

6º (АÈВ) ÇС=(АÇС)È(ВÇС) (дистрибутивность Ç-я отн-но объединения) 7º (АÇВ) ÈС=(АÈС) Ç (ВÈС)

8º(АÈВ) ÇА=А 9º (АÇВ) ÈВ=А }з-ны поглощения

Объединением мн-в А и В наз мн-во, содержащее те и только те эл-ты, кот принадл хотя бы 1 из этих мн-в.

А= {1,2,3} В={3,4,5}

АÈВ={1,2,3,4,5}Эл-т не может встречаться дважды.

А=N, В={0} АÈВ= N0 -мн-во целых неотриц чисел.

Теорема о cв-вах объединения.

1ºАÈВ= ВÈА (коммут) 2º(АÈВ) ÈС=АÈ(ВÈС) (асс)

3º АÈА=А (идемпотентность) 4º АÈÆ=А

5º Если АÌВ, то АÈВ=В (большему из них)

Док-во 5º: Усл: АÌВ Док-ть АÈВ=В Докажем сначала, что ВÌ АÈВ – это очевидно (по опр.),

Докажем обратное вкл-е: АÈВÌВ. Пусть хÎ АÈВ, тогда хÎА или хÎВ. Если хÎА, то с учетом дано хÎВ.

Если хÎВ, то хÎВ. Во всех случаях х явл-ся эл-том В (хÎВ) ч.т.д.По критерию равенства мн-в АÈВ=В ч.т.д.

Разностью (А\В) мн-в А и В наз А\В состоящая из тех и только тех эл-тов мн-ва А, кот. не явл-ся эл-тами В.

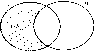
Теорема о cв-вах вычитания.

1º А\Æ =А (Æ – прав нейтральный эл-т вычитания)

2º Æ\ А=Æ 3º А\А=Æ 4ºА\В=А\(АÇВ)

5ºА\ (АÈВ)=Æ 6º А\ (А\В)= АÇВ=В\ (В\А)

7º А\ (В\А)=А 8º (А\ В) ÈА, (А\В) ÈВ=АÈВ.

Симметрической разностью мн-в А и В наз мн-во АDВ, состоящее из тех и только тех эл-тов, которые Îили мн-ву А или мн-ву В.

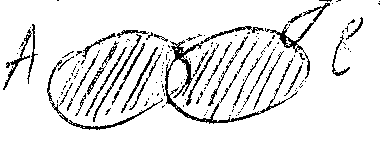Теорема о cв-вах симм. вычит.

1ºАDВ=ВDА 2º(АDВ)DС=АD(ВDС) (ассоц)

3ºАDА=Æ 4ºАDÆ=А 5ºАD (АDВ)=В

6º АDВ = (АÈВ)\ (АÇВ)=(А\ В) È (В\ А)

Дополнением мн-ва В до мн-ва А наз мн-во, содерж те и только те эл-ты мн-ва А, кот не принадлеж мн-ву В.

Дополнение мн-ва до универсального.

Пусть U- универсальное мн-во. Все мн-ва его подмн-ва. Тогда для подмн-ва универсального мн-ва U его дополнением Ā наз Ā= U\А.

Теорема о cв-вах дополнения.

1º двойное отрицание А=А (инволютивность)

2º отрицание АÈВ= Ā Ç отрицание В }з-ны

3º А Ç В= Ā È отрицание В де Моргана

4º А È Ā = U 5º Æ = U 6º отрицание U = Æ

Декартовым умножением мн-в А и В наз мн-во АCВ, состоящее из всех упорядоченных пар (а,b), где а ÎА, bÎВ. Можно перечислить пары или взять 2 мн-ва.

А={2,3,5} В = {-1, 0,4,6} АCВ = {(2,-1), (2,0), (2,4), (2,6), (3,-1), (3,0), (3,4), (3,6), (5,-1), (5,0), (5,4), (5,6) }.