Логические задачи и логические парадоксы (антиномии).

Задача: Трое друзей нашли старинный сосуд. Первый сказал, что это греческий сосуд IV века, второй – что это финикийский сосуд III века, третий – что это негреческий сосуд V века. В итоге каждый оказался прав лишь наполовину. Какого века сосуд?

Решение

Пусть G: сосуд греческий; F: сосуд финикийский; А: он IV века; В: он III века; С: он V века Т.к. каждый оказался прав наполовину, то {GvA = И = FvB = ͞GvC, {GʌA = Л=FʌB= ͞GʌC Решаем систему перебором по происхождению.

Пусть G=И, значит F=Л. Тогда {ИvА = И = ЛvВ = ЛvС {ИʌА = Л =ЛʌВ=ЛʌС А из ИʌА=Л А=Л В из И = ЛvВ В=И С из И= ЛvС С=И

2. Пусть G=Л, значит F=И. Тогда {ЛvА = Л = ИvВ = ИvС {ЛʌА = И =ИʌВ=ИʌС Из А=И подставляем вниз Из Л= ИʌВ получаем В=Л Из ИʌС=Л → С=Л Ответ: сосуд финикийский и он IV века.

Парадо́кс — ситуация (высказывание, утверждение, суждение или вывод), которая может существовать в реальности, но не имеет логического объяснения.

Понятие и примеры множеств. Равные множества. Конечные и бесконечные множества. Числовые множества. Диаграммы Эйлера и их применения. Способы задания множеств.

Множество (неопределяемое понятие) – совокупность предметов, объединенных в одну какую-л группу (прописными буквами ла­тинского алфавита: А, В, С, ... , Z).

Мн-во, не содержащее ни одного объекта, называется пустым (Æ).

Объекты, из кот образовано мн-во, называются элементами (строчными бук­вами латин алфавита: а, Ь, с, ... , Z)..

Мн-ва бывают конечные и бесконечные. Эти понятия мы принимаем без определения. Конечными явл-ся мн-во дней недели, месяцев в году, а бесконечными – мн-во точек на прямой, мн-во натуральных чисел.

Для ряда числовых мн-в в матем приняты стандартн обозначения: N – мн-во натур чисел (исп. при счете); Z – мн-во целых чисел (исп при счете, отриц и ноль); D – дробных; О – отриц чисел; Q – мн-во рациональных (целые и дроби); J- мн-во иррациональных; R – мн-во действител.

Способы задания мн-ва. Мн-во определяется своими элементами, т.е. мн-во задано. если о любом объеюпе можно сказать, принадлежит он этому множеству или не принадлежит..

1) Множество можно задать, перечислuв все его элементы. Н-р, мн-во А состоит из чисел 3, 4, 5 и 6: запись, в которой перечисляемые элементы заключаются в фигурные скобки: А = {З, 4, 5, 6}.

Мн-во гласн букв рус яз.{а, е, ё, и, о, у, э, ю, я, ы}

2) указывают ха­рактеристическое свойство его элементов-такое св-во, кото­рым обладает кажд элемент, принадлежащий мн-ву, и не обладает ни один элемент, кот ему не принадл. Мн-во А двузн чисел: св-во, которым обладает кажд эл-т дан мн-ва, - «быть двузн числом». Так, число 45 содержится в мн-ве А, поскольку оно дву­зн, а число 145 мн-ву А не принадл, т.к. оно не явл-ся двузн.

А = {12, 22, 32,42, 52, 62, 72, 82, 92}.

Решение. Перечислены все эл-ты мн-ва А. Их характеристическое св-во: «быть двузначным и оканчи­ваться цифрой 2».

Равные мн-ва – если они состоят из одних и тех же эл-тов. (А=В, АÌВ, ВÌА).

Множество В явл-ся подмн-вом мн-ва А, если кажд эл-т мн-ва В явля­ется также эл-том мн-ва А. Пустое мн-во считают подм-вом любого мн-ва. Любое мн-во – подмн-во самого себя.

Отношения между множествами наглядно представляют при помощи особых чертежей, называемых кругами Эйлера Леонарда. Диаграмма Эйлера-Венна - рисунок, чертеж, диа – через, при помощи.

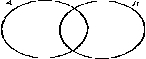
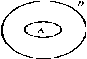
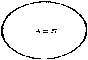
А=В(4), АÌВ(3), ВÌА(2), АÇВ(1)