Операции над высказываниями : дизъюнкция, конъюнкция, отрицание, импликация, эквиваленция, разделительная дизъюнкция, штрих Шеффера, стрелка Пирса. Свойства.

Понятие высказывания. Простые и составные высказывания. Равные высказывания. Таблица истинности и их применения.

Основным (неопределяемым) понятием математической логики является понятие «простого высказывания».

Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».

Приведем примеры высказываний.

1) Санкт –Петербург стоит на Неве.

2) Париж — столица Англии.

3) Карась не рыба.

4) Число 6 делится на 2 и на 3.

5) Если юноша окончил среднюю школу, то он получает аттестат зрелости.

Высказывания 1), 4), 5) истинны, а высказывания 2) и 3) ложны.

Очевидно, предложение «Да здравствуют наши спортсмены!» не является высказыванием.

Различают два вида высказываний.

Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным.

Примерами элементарных высказываний могут служить высказывания 1) и 2).

Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если .... то ...», «тогда и только тогда», принято называть сложными или составными.

Так, высказывание 3) получается из простого высказывания «Карась - рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на З», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки «если ..., то ...». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда».

В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

Элементарные высказывания обозначаются малыми буквами латинского алфавита: х, у, z, ..., а, b, с, ...; истинное значение высказывания цифрой 1, а ложное значение - буквой цифрой 0.

Если высказывание а истинно, то будем писать а = 1, а если а ложно, то а = 0.

Виды теорем и связь между ними. Примеры.

Теорема - это высказывание, истинность которого уста­навливается посредством рассуждения (док-ва).

С логической т. зр теорема предст собой вы­сказывание вида А Þ В, где А и В - высказывательные формы с одной или неск переменными. Предложение А на­з условиемтеоремы, а предложение В – ее заключением.

Например, условием теоремы «если четырехугольник яв­л-ся прямоугольником, то в нем диагонали равны» является предложение «четырехугольник - прямоугольник», а заключением - предложение «в таком четырехугольнике диа­гонали равны».

Для всякой теоремы вида «если А, то В»можно сформ-ть предложение «если В, то А», кот наз обрат­ным данному. Однако не всегда это предложение явл-ся теоремой. Рассмотрим теорему «в равнобедренном D углы при основании равны». Обратное ей предложение таково: «если в D углы при основании равны, то этот D- равнобедр». Оно, ис­тинное и поэт явл-ся теоремой. Ее наз теоремой, обратной данной.

Для всяк теоремы вида «если А, то В» можно сф-ть предложение «если не А, то не В», кот наз противоположным данному. Но не всегда это предлож явл-ся теоремой. Н-р, предложение, противоположное теореме «если четырехуг-к явл-ся прямоугольником, то в нем диагонали равны», будет ложным: «если четырехугольник не явл-ся прямоугольником, то в нем диагонали не равны». В том случае, если предложение, противоположное дан­ному, будет истинно, его наз теоремой, противопо­ложной данной.

Для всякой теоремы вида «если А, то В» можно сформ-ть предложение «если не В, то не А», кот наз обратным противоположному. Н-р, для теоремы «если четырехуг-к явл-ся прямоуг-ком, то в нем диаго­нали равны» предложение, обратное противоположному, будет таким: «если в четырехуг-ке диагонали не равны, то он (четырех-к) не явл-ся прямоуг-ком». Предложение истинное и, след-но, явл-­ся теоремой. Ее наз обратно противоположной данной.

Пред­ложения, обратные противоположным, всегда будут тео­ремами, п.ч. имеется след равносильность (АÞВ) Û (отрицание ВÞĀ).

Эту равносильность называют законом контрапозиции.

Мы принимаем его без док-ва. Согласно этому з-ну, предложение, обратно противоположное какой-л теореме, также явл-ся теоремой, и, значит, вместо дан теоремы можно док-ть теорему, обратно противополож

ную данной. Кроме того, из з-на контрапозиции следует, что пред­ложение, обратное данному, и предложение, противополож­ное данному, одновременно истинны либо одновременно ложны. Поэт, рассматривая их, достаточно док-ть (или опровер) какое-н одно; тем самым будет док-но (опровергнуто) и второе.

Если для дан теоремы АÞВ существует обратная В Þ А, то их можно объединить в одну А Û В, и то­гда в формулировке будут исп-ся слова «необходимо и достаточно», «тогда и только тогда, когда». Например, объ­единение теоремы «в равнобедр D углы при основании равны» и «если в D углы при основа­нии равны, то D - равнобедрен» в одну, полу­чим теорему: «D будет равнобедренным тогда и только тогда, когда в нем углы при основании равны».

Можно сформулировать ее иначе: «для того, чтобы D был равнобедренным, необходимо и достаточно, чтобы в нем углы при основании были равны».

С др стороны, если теорема им вид равносильности А Û В, то это значит, что она состоит из двух взаимно обрат­ных теорем А Þ В и В Þ А и, следовательно, ее док-­во сводится к док-ву двух указанных теорем.

Если усл или заключение дан теоремы предст собой конъюнкцию или дизъюнкцию, то, чтобы получить предложение, противоположное данному, нужно учитывать правила построения отрицания конъюнк­ции и дизъюнкции. Н-р, дана теорема «если число де­лится на 3 и 4, то оно делится на 12». Предложение, противо­положное данному, можно сформулировать так: «если число не делится на 12, то оно не делится на 3 или не делится на 4».

Основные понятия. Примеры.

Говорят, что между мно-вами А и В задано соответствие f, если хотя бы одному элементу из А соответствует что-то из В.

a f b (b=f(a), a→b). элементу а из А по закону f соответствует b из В.

Множество всех преобразований называется областью определения соответствия f и обозначается D(f).

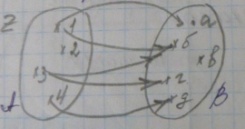Граф соответствия f – это

Мы видим, что 1 f a, 1 →б, б=f(3), 3fг, 4fд, а также, что D(f) = {1,3,4}, E(f) = {а, б, г, д}.

Понятно, что (область определения часть) D(f) c A, E(f) c B.

График соответствия f – это множество G(f) всех пар вида (a.b), где a f b. Понятно, что G(f) c AxB

У нас G(f) = {(1,a), (2, б), (3, г), (4, д)}

Примеры биекций . свойства биекций.

Определения. 1) Если f одновременно всюду определено и функция, то f – отображением A в B. (На графе: из каждой точки A только одна стрелка. f – всюду определенное (D(f)=A. На графе: из каждой точки A должна выходить хотя бы одна стрелка.)).

2) Соответствие f – биекция (f одновременно сюръекция, функция и инъекция (равночисленность множеств). f – сюръекция (E(f)=B. На графе: к каждой точке B должна подходить хотя бы одна стрелка). f – функция (у каждого элемента из A не более одного образа в B (1 или 0). На графе: из каждой точки A выходит не более 1 стрелки). f – инъекция (у каждого элемента из B не более 1 прообраза в A. На графе: к каждой точке B подходит не более 1 стрелки).).

Примеры биекции: 1) Если f – биекция между конечными множествами A и B, то можно понять, что эти множества должны быть равночисленными (|A|=|B|).

2) N: 1, 2, 3, 4, 5, …; N₀: 0, 1, 2, 3, 4, …; f(n)=n-1 (биекция) не трудно убедиться, что f – биекция, проверяем является ли оно сюръекцией, функцией и инъекцией).

3) N: 1, 2, 3, 4, 5, …; N₂: 2, 4, 6, 8, 10, …; f(n)=2n (биекция)

4) N и веревка с узлами. Биекция между N и узлами этой веревки устанавливается легко.

Равномощность множеств. Примеры. Счётные множества и множества мощности континуум.

Рассмотрим два множества A и B.

Отображение ƒ из A в B (обозначается ƒ: A→B) — это правило, которое каждому элементу множества A ставит в соответствие элемент множества B, причём ровно один. (При этом не запрещается двум элементам множества A ставить в соответствие один и тот же элемент множества B, рис. 1, а.)

Отображение ƒ называется взаимно однозначным, если каждый элемент множества B поставлен в соответствие ровно одному элементу множества A (рис. 1, б).

Множества A и B называются равномощными, если существует взаимно однозначное отображение ƒ:A→B. Понимать это можно так: множества равномощны, если в них одинаковое количество элементов.

Например, множества {0, 1, 2} и {лошадь, корова, телевизор} равномощны, а множества {0, 1, 2} и {лошадь, корова} неравномощны (телевизор был по делу...).

Определение Множества, эквивалентные по числу элементов множеству N={1, 2, 3, 4, …} называются счетными множествами.

Примеры счетных множеств:

{2, 4, 6, 8, …}; ;{1, 4, 9, 16, 25, …}; {1, 8, 27, 64, 125, …}

Свойства счетных множеств изложим, пользуясь терминологией математики, т.е. громко именуя их теоремами.

Теорема 1. Для того, чтобы множество А было счетным, необходимо и достаточно, чтобы его можно было представить в виде А={a1, a2, a3,…}

Бинарные отношения на множестве. Примеры. Частные виды. Особенности графов и матриц.*⁾

Определение. Про соответствие f между множествами A и B в случае, когда эти множества равны (A=B), можно говорить, что это бинарное отношение на множестве A. Таким образом бинарное отношение это частный случай соответствия. Поэтому для бинарных отношений справедливо все, что верно для соответствий.

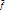Примеры. 1) A=N Пусть afb, если a b. Например, 1f1, но 1 2, 13f1, но 13 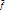7.

2) A – тоже, но afb, если натуральное a кратно простому b. Это другой пример, так как здесь на втором месте не может быть 1, т.к. оно не простое (простое – N, у которого ровно 2 делителя; составное – N, у которого больше двух делителей).

3) A={1, 2, 3, …, 9} Пусть afb, если a≤b. Например, 0≤ любого b, любое a≤9, но 3 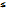2.

Определения. 1. f называется рефлексивным отношением, если всегда afa, т.е. любой элемент a находится в отношение f сам с собой. На графе такого отношения каждая точка снабжена петлей.

Примеры. 1) Быть кратным на N (но не на N₀). 2) Быть родственниками. 3) Быть не выше (но не «быть выше»).

2. В последнем случае, когда всегда a не f a, говорят что f антирефлексивно. В этом случае на графе нет ни одной петли.

3. f называется симметричным отношением, если из afb всегда следует bfa. На графе все стрелки вот такие:↔.

4. Если же для различных a и b из afb всегда следует b не f a, то такое f называют антисимметричным.

Примеры. 1) быть знакомыми, 2) быть одного возраста, 3) учиться в одном классе, 4) иметь одних и тех же родителей и т.д., 5) быть мамой своего ребенка, 6) быть длиннее на множестве отрезков.

5. f называется транзитивным отношением, если из afb,bfc всегда следует afc. На графе все цепочки должны быть замкнуты.

6. Если же f одновременно рефлексивно, симметрично и транзитивно, то оно называется отношением эквивалентности.

Примеры. 1) Учиться в одном классе. 2) Родиться в одном и том же году или в одном и том же месте. 3) Начинаться с одинаковой буквы, но не иметь «хотя бы одну» одинаковую букву (мама f мыла, мыла f рыльце, но мама не f рыльце).

Отношение эквивалентности. Примеры. Класса эквивалентности.

Отношение R на мн-ве Х наз отношением эквивалент

ности, если оно одновременно обладает cв-вами рефлексивности, симметричности и транзитивности.

Если на .мн-ве Х задано отношение эквuва лентности, то оно порождает разбиение этого мн-ва на попарно непересекающиеся подмн-ва (классы эквива­лентности).

Бинарным отношением на мн-ве Х наз всякое подмн-во декартова произведения ХCХ.

1º R рефлексивно на Х Û хRх для любого хÎХ. P

2º симметрично хRу Û уRу (туда-сюда)

3º транзитивности хRу, уRz } хRz хªу, уªz I хªz

Классы: 1. элементы одного класса эквивалентности взаимозаменяемы. Так в дробь 3/6 можно заменить на ½.

2. класс эквивалентности опр-ся любым своим представителем

3. разбиение мн-ва на классы исп-ся для введения новых понятий.

Отношение R на мн-вe Х наз отношением порядка, если оно одновременно обладает св-вом антисuмметричности и транзитивности. Примеры: отношения «меньше» на мн-ве N, «короче» на мн-ве отрезков.

Теорема. 1. Каждое отношение эквивалентности порождает разбиение мн-ва на классы, подчиненное данному отношению.

Теорема. 2. Если есть разбиение на мн-ва М на классы, то существует отношение эквивалентности на этом мн-ве М, которому подчинено данное разбиение.

Отношения порядка. Примеры.

Определение. Бинарное отношение f на M называется отношением порядка, если f транзитивно и антисимметрично (т.е. для различных a и b из afb всегда следует bfa). Можно сказать что из afb и bfa всегда следует, что a=b.

Примеры. 1) N₀={0, 1, 2, 3, …}. Отношения >, <, ≤, ≥ транзитивны и антисимметричны (a>b следовательно b>a). 2) A – все студенты. Пусть afb, если a – не старше b (выше, тяжелее, веселее и т.д.). Если под «не старше» понимать что человек a родился в тот же день, что и b, или позже, то антисимметричности нет, т.к. есть «нарушители» - «однодневки». Если учитывать еще и время рождения, то это отношение антисимметрично. 3) T – множество треугольников. afb, если S_a>S_b. f – транзитивно и антисимметрично. 4) 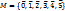. Попробуем ввести в этом множестве отношение порядка. 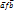, если a<b – порядок. 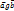, если a и b взаимно простые числа. g – не транзитивно. Контрпример: 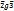, , 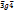но .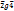

Частные виды порядков: Определения. Порядок f называется строгим, если он антирефлексивен, т.е. всегда afa. Порядок f называется нестрогим, если он рефлексивен.

Примеры. В рассмотренных выше примерах строгими будут из 1) отношения <, >; отношения порядка из 3) и из 4). К нестрогим порядкам относятся из 1) примера отношения ≤, ≥; из 2) примера отношения порядка.

Определение. Порядок f называется линейным, если для любых различных a и b справедливо afb или bfa.

Примеры. Порядок из примера 1) будет строгим (<, >) или нестрогим (≤, ≥) линейным порядком; порядок из 2) примера.

БАО как отображение МxМ М. Свойства и примеры БАО.

Определение. Если на некотором множестве M задан закон, по которому любым двум элементам a и b из M (может быть a=b) сопоставляется вполне определенный элемент a*b из этого же множества то говорят, что на M задана бинарная алгебраическая операция *.

Примеры. 1) сложение и вычитание на множестве всех векторов, 2) конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, штрих Шеффера и стрелка Пирса на множестве всех высказываний, 3) сложение, умножение, вычитание и деление на множестве целых чисел, 4) объединение, пересечение, разность множеств, декартово произведение множеств.

Свойства:

1) Коммутативность. БАО коммутативно, если для любых а и b из M выполняется равенство а*b=b*а. Примеры. 2∙5=5∙2.

2) Ассоциативность. БАО ассоциативно, если для любых а, b и c из M выполняется равенство (а*b)*c=а*(b*c). Примеры. (4+7)+9=4+(7+9).

3) Идемпотентность. БАО идемпотентно, если для любого а из M выполняется равенство а*а=а. Примеры. 1∙(:)1=1, 0+0=0.

4) Нейтральный и поглощающий элементы (левый, правый, просто). Нейтральный элемент e из множества M относительно БАО, если для любого элемента a из M выполняется равенство e*a=a или a*e=a. Примеры. 2+0=0+2=2 (для сложения в Z – 0), 2∙1=1∙2=2 (для умножения в Z – 1), 2-0=2 (правый нейтральный элемент для вычитания).

Поглощающий элемент e из множества M относительно БАО, если для любого элемента a из M выполняется равенство e*a=е или a*e=е. 2∙0=0∙2=0 (для сложения в Z – 0), 0:2=0 (левый поглощающий элемент для вычитания).

5) Дистрибутивность (левый, правый, просто). БАО ◦ дистрибутивно относительно БАО *, если для любых элементов а, b и c из M выполняются равенства (a*b)◦c=(a◦c)*(b◦c), c◦(a*b)=(c◦a)*(c◦b). Примеры. (1+3)∙6=(1∙6)+(3∙6), 6∙(1+3)=(6∙1)+(6∙3).

6) Закон поглощения. Если для любых а и b из M выполняется равенство (a*b)◦a=a◦(a*b)=a, то это закон поглащения. Примеры. (АvВ)ʌA=Aʌ(АvВ)=A (на множестве высказываний).

Понятие УАО на множестве M. Примеры. Свойства УАО: инволютивность + закон А. де Моргана (1806-1871) в логике и теории множеств + законы исключенного третьего (Tertium non datur) и противоречия (там же).

УАО как (~5 вопросов по лекциям).

Определение. Если на некотором множестве M задан закон, по которому любому элементу a из M сопоставляется вполне определенный элемент a* из этого же множества то говорят, что на M задана унарная алгебраическая операция *.

Примеры. 1) отрицание высказываний, 2) дополнение множества до универсального, 3) центральная и осевая симметрия.

Свойства:

1) Инволютивность. УАО инволютивно, если для любого а из M выполняется равенство а*=а. Примеры. 1) U=N (U – универсальное множество). Для множества N₂ его дополнением до универсального будет множество , в свою очередь его дополнением до универсального будет 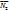, а по свойству N₂= 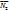. 2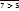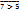) 7>5, , =7>5.

2) Закон де Моргана. Если для любых а и b из M выполняется равенство (a◦b)*=a*▫b*=a, то это закон де Моргана. Примеры. 1) , 2) .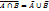

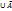3) Закон исключенного третьего. Если для любых а из M выполняется равенство a◦а*=е, то это закон исключенного третьего. Примеры. 1) Аv =И, 2) А =U.

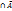4) Закон противоречия. Если для любых а из M выполняется равенство a◦а*=е, то это закон противоречия. Примеры. 1) Аʌ =Л, 2) А =Ø.

Примеры комбинаторных задач

Определение. В обыденной жизни нам не редко встречаются задачи, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число. Задачи требующие такого решения, называют комбинаторными.

Примеры: 1) Сколько квадратов на рисунке? (всего 5)

2) Сколько здесь прямоугольников? (1×1-4, 2×1-2, 1×2-2, 2×2-1 всего 9)

3) Сколько треугольников на рисунке?

Понятие высказывания. Простые и составные высказывания. Равные высказывания. Таблица истинности и их применения.

Основным (неопределяемым) понятием математической логики является понятие «простого высказывания».

Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».

Приведем примеры высказываний.

1) Санкт –Петербург стоит на Неве.

2) Париж — столица Англии.

3) Карась не рыба.

4) Число 6 делится на 2 и на 3.

5) Если юноша окончил среднюю школу, то он получает аттестат зрелости.

Высказывания 1), 4), 5) истинны, а высказывания 2) и 3) ложны.

Очевидно, предложение «Да здравствуют наши спортсмены!» не является высказыванием.

Различают два вида высказываний.

Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным.

Примерами элементарных высказываний могут служить высказывания 1) и 2).

Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если .... то ...», «тогда и только тогда», принято называть сложными или составными.

Так, высказывание 3) получается из простого высказывания «Карась - рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на З», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки «если ..., то ...». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда».

В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

Элементарные высказывания обозначаются малыми буквами латинского алфавита: х, у, z, ..., а, b, с, ...; истинное значение высказывания цифрой 1, а ложное значение - буквой цифрой 0.

Если высказывание а истинно, то будем писать а = 1, а если а ложно, то а = 0.

Операции над высказываниями : дизъюнкция, конъюнкция, отрицание, импликация, эквиваленция, разделительная дизъюнкция, штрих Шеффера, стрелка Пирса. Свойства.

Импликация (условное суждение) - лог. связка "Если…, то…" Обычно обозначается знаком "→".
"Если перерезать провод, то лампа погаснет" - первое суждение "перерезать провод" называется основание (антецендент), второе - "лампа погаснет" - следствие (консеквент).

Таблица истинности для импликации

p	q	p→q
и	и	и
и	л	л
л	и	и
л	л	и

Импликативные суждения истинны во всех случаях, кроме одного когда антецедент - истинен, а консеквент - ложен. То есть в случае, когда причина возникла, а следствие не наступает, вся импликация является ложной. Зависимость между основанием и следствием характеризуется свойством достаточности: истинность основания обусловливает истинность следствия (1-я строка таблицы), но не необходимости: при ложности основания следствие может быть как истинным, так и ложным (3-я и 4-я строки в таблице).
"Если плохо одевать зимой, то можно заболеть" - если основание ложно, то следствие неопределенно. Возьмем те же высказывания Р и Q. С помощью импликации составим новое высказывание: Р→Q – «Если Вася выучил теорему, тоон получил пятерку»,или«из того что Вася выучил теорему , следует что он получил пятерку».

Высказывание Р→Q – «Если Вася выучил теорему, тоон получил пятерку» будет ложно только если предпосылка Р будет истинна, а заключение Q – ложно (см. таблицу).Если высказывание Р→Q истинно, то говорят, что Р логически следует из Q, обозначается РÞQ.

Конъюнкциейвысказываний А u В называет­ся высказывание А Λ В, которое истинно, когда оба выска­зыванuя истинны, и ложно, когда хотя бы одно из этих высказываний ложно.

Дизъюнкциейвысказываний А и В называет­ся высказывание А v В, которое истинно, когда истинно хотя бы одно изэтих высказываний, и ложно, когда оба высказывания ложны. КОНЪЮНКЦИЯ

А	В	АΛВ
и	и	и
и	л	л
л	и	л
л	л	л

«Число 28 делится на 7 и на 9» конъюнкция, первое истинно, второе ложно, поэт высказывание ложно (по опр.).

1ºАΛВ=ВΛА(коммутативность)

2º (А ΛВ) Λ С=А Λ(В ΛС) (ассоц-ть)

3º А ΛА=А

4ºА Λ и= А

5ºА Λл= л

6º(А vВ) ΛС= (А ΛС)v (В ΛС) дистрибу-

тивность конъюнкции относ-но дизъюнкции

7º(А ΛВ) v С= (А vС)Λ (В vС) дистрибу-

тивность дизъюнкции относ-но конъюнкции

8º(А ΛВ) v А=Акто больше съел того, кого

9º(А vВ) Λ А=Аменьше

ДИЗЪЮНКЦИЯ

А	В	АvВ
и	и	и
и	л	и
л	и	и
л	л	л

«Число 28 делится на 7 или на 9», «15 кратно 3» -истинно.

1ºАvВ=ВvА(коммутативность)

2º (АvВ) v С=Аv(ВvС) (ассоциативность)

3º АvА=А

4ºАv и= и

5ºАv л= А

Отрицание – логическая связка, с помощью которой из данного высказывания получается новое высказывание, такое, что если исходное высказывание истинно, его отрицание является ложным, и наоборот. Отрицательное высказывание состоит из исходного высказывания и отрицания, выражаемого обычно словами «не», «неверно, что». Отрицательное высказывание является, таким образом, сложным высказыванием: оно включает в качестве своей части отличное от него высказывание. Например, отрицанием высказывания «10 – четное число» является высказывание «10 не есть четное число» (или: «Неверно, что 10 есть четное число»). Обозначим высказывания буквами А, В, С,... Полный смысл понятия отрицания высказывания задается условием: если высказывание А истинно, его отрицание ложно, и если А ложно, его отрицание истинно. Например, так как высказывание «1 есть целое положительное число» истинно, его отрицание «1 не является целым положительным числом» ложно, а так как «1 есть простое число» ложно, его отрицание «1 не есть простое число» истинно.

Эквиваленцей (или эквивалентностью) двух высказываний х и у называется новое высказывание, которое считается истинным, когда оба высказывания х, у либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.

Эквиваленция высказываний х, у обозначается символом х ↔у , читается «для того, чтобы х, необходимо и достаточно, чтобы у» или «х тогда и только тогда, когда у». Высказывания х, у называются членами эквиваленции.

Логические значения операции эквиваленции описываются следующей таблицей истинности:

Например, эквиваленция: «Треугольник SPQ с вершиной S и основанием PQ равнобедренный тогда и только тогда, когда SP = SQ » является истинной, так как высказывания «Треугольник .SPQ с вершиной S и основанием PQ равнобедренный» и «В треугольнике SPQ с вершиной S и основанием PQ SP = SQ » либо одновременно истинны, либо одновременно ложны.

Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.

Разделительная дизъюнкция высказываний А ΛВ является высказывание А В.

А	В	А В
И	И	Л
И	Л	И
Л	И	И
Л	Л	Л

1 º А В = В А

2 º (А В) С = А (В С)

3 º А А = л

4 º А И = А

Штрих Шеффера и стрелка Пирса

Штрихом Шефера (отрицание конъюнкции) высказываний А и В наз-ся выск. А│В (штрих) с таблицей истинности

АВ	А│В
ии	л
ил	И
ли
лл

Св-ва

1) А│В = В│А (коммутативность)

2) (А│В)│С = А│(В│С) (ассоциативность)

3) А│А = А ۸ А = А (нет идемпотентности)

4) А│И = А

И│В = ¯͞В

А│Л = И

Л│В = И

(ни того, ни другого)

Эта операция обладает одним единственным свойством: через неё можно выразить все остальные логические операции.

В силу свойства 3) ͞А = А│А.

Т.к. А│В = Аʌ͞͞В (-), то АʌВ = ͞А│͞В (-) → АʌВ = А│В (-) = (А│В) │(А│)

АvВ (-) = (з.дм.) = ͞Аʌ͞ ͞В → АvВ = ͞А v͞ ͞В (-) = (͞А ʌ ͞В) │ (͞А ʌ ͞В) и т.д.

Стрелкой Пирса (отрицание дизъюнкции) высказываний А и В называется высказывание А↓В (стрелка) с таблицей истинности

АВ	А↓В
ии	Л
ил
ли
лл	и

Видим, что А↓В = АvВ (-), А↓В (-) = АvВ т.о. А↓В = АvВ (-) =(з.дм.) ͞Аʌ͞͞ ͞В

А↓В озвучивается как «ни то, ни сё». Через стрелку Пирса выражаются все остальные логические операции.

͞x ≡ x↓x

x ʌ y ≡ (x↓x) ↓ (y↓y)

x ∨ y ≡ (x↓y) ↓ (x↓y)

x → y ≡ ((x↓x) ↓ y) ↓ ((x↓x) ↓ y)

(Возможен вариант с А и В)

Виды теорем и связь между ними. Примеры.

Теорема - это высказывание, истинность которого уста­навливается посредством рассуждения (док-ва).

С логической т. зр теорема предст собой вы­сказывание вида А Þ В, где А и В - высказывательные формы с одной или неск переменными. Предложение А на­з условиемтеоремы, а предложение В – ее заключением.

Например, условием теоремы «если четырехугольник яв­л-ся прямоугольником, то в нем диагонали равны» является предложение «четырехугольник - прямоугольник», а заключением - предложение «в таком четырехугольнике диа­гонали равны».

Для всякой теоремы вида «если А, то В»можно сформ-ть предложение «если В, то А», кот наз обрат­ным данному. Однако не всегда это предложение явл-ся теоремой. Рассмотрим теорему «в равнобедренном D углы при основании равны». Обратное ей предложение таково: «если в D углы при основании равны, то этот D- равнобедр». Оно, ис­тинное и поэт явл-ся теоремой. Ее наз теоремой, обратной данной.

Для всяк теоремы вида «если А, то В» можно сф-ть предложение «если не А, то не В», кот наз противоположным данному. Но не всегда это предлож явл-ся теоремой. Н-р, предложение, противоположное теореме «если четырехуг-к явл-ся прямоугольником, то в нем диагонали равны», будет ложным: «если четырехугольник не явл-ся прямоугольником, то в нем диагонали не равны». В том случае, если предложение, противоположное дан­ному, будет истинно, его наз теоремой, противопо­ложной данной.

Для всякой теоремы вида «если А, то В» можно сформ-ть предложение «если не В, то не А», кот наз обратным противоположному. Н-р, для теоремы «если четырехуг-к явл-ся прямоуг-ком, то в нем диаго­нали равны» предложение, обратное противоположному, будет таким: «если в четырехуг-ке диагонали не равны, то он (четырех-к) не явл-ся прямоуг-ком». Предложение истинное и, след-но, явл-­ся теоремой. Ее наз обратно противоположной данной.

Пред­ложения, обратные противоположным, всегда будут тео­ремами, п.ч. имеется след равносильность (АÞВ) Û (отрицание ВÞĀ).

Эту равносильность называют законом контрапозиции.

Мы принимаем его без док-ва. Согласно этому з-ну, предложение, обратно противоположное какой-л теореме, также явл-ся теоремой, и, значит, вместо дан теоремы можно док-ть теорему, обратно противополож

ную данной. Кроме того, из з-на контрапозиции следует, что пред­ложение, обратное данному, и предложение, противополож­ное данному, одновременно истинны либо одновременно ложны. Поэт, рассматривая их, достаточно док-ть (или опровер) какое-н одно; тем самым будет док-но (опровергнуто) и второе.

Если для дан теоремы АÞВ существует обратная В Þ А, то их можно объединить в одну А Û В, и то­гда в формулировке будут исп-ся слова «необходимо и достаточно», «тогда и только тогда, когда». Например, объ­единение теоремы «в равнобедр D углы при основании равны» и «если в D углы при основа­нии равны, то D - равнобедрен» в одну, полу­чим теорему: «D будет равнобедренным тогда и только тогда, когда в нем углы при основании равны».

Можно сформулировать ее иначе: «для того, чтобы D был равнобедренным, необходимо и достаточно, чтобы в нем углы при основании были равны».

С др стороны, если теорема им вид равносильности А Û В, то это значит, что она состоит из двух взаимно обрат­ных теорем А Þ В и В Þ А и, следовательно, ее док-­во сводится к док-ву двух указанных теорем.

Если усл или заключение дан теоремы предст собой конъюнкцию или дизъюнкцию, то, чтобы получить предложение, противоположное данному, нужно учитывать правила построения отрицания конъюнк­ции и дизъюнкции. Н-р, дана теорема «если число де­лится на 3 и 4, то оно делится на 12». Предложение, противо­положное данному, можно сформулировать так: «если число не делится на 12, то оно не делится на 3 или не делится на 4».