Двоичные суммирующие счетчики.

Схему двоичного суммирующего счетчика можно построить используя двухтактный Т-триггер (см. рис. 4.1). Известно, что Т-триггер меняет свое состояние тогда и только тогда, когда значение на входе “T” равно логической “1”, и по следующему синхроимпульсу значение выхода “Q” Т-триггера изменится на противоположное.

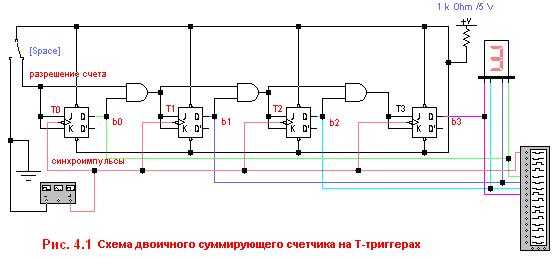
На схеме функции, определяющие значение входов Т, формируются цепочкой 2-х входовых логических элементов “И” (“2И”), т.е. элементов, выполняющих логическую функцию “И” и имеющих два входа.

Нетрудно заметить, что счетчик расширяется до любого количества разрядов простым добавлением элементов “2И” и Т-триггера на каждый двоичный разряд.

На вход То счетчика подается сигнал “разрешение счета”.

Если на эту линию подана логическая “1”, то на все входы поступают сигналы, нужные для перехода триггеров счетчика в следующее состояние.

Если на ней логический “0”, то на всех входах будет так же логический “0”, и триггеры не изменят своего состояния.

Изображенный счетчик называется синхронным, т.к. каждый импульс на общей синхронизирующей линии вызывает переход к следующему состоянию в счетной последовательности всех триггеров счетчика.

Для того чтобы в этом убедиться, построим временную диаграмму функционирования синхронного счетчика (рис. 4.2).

Точки 1 и 2 на приведенной диаграмме показывают, что после прохождения очередного синхроимпульса следующий синхроимпульс нельзя подавать до тех пор, пока не определятся все значения на входах Т_i.

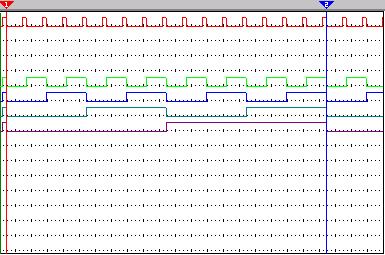
Рис. 4.2

Двоичные вычитающие счетчики.

До сих пор мы рассматривали только суммирующие счетчики. Эти счетчики производили изменение выходов bо…b3 в соответствии с известной таблицей:

b3	b2	b1	b0	Десятичная цифра

Очевидно, что значение i-го разряда меняется всегда, когда текущие значения всех младших (от 0 до i-1) разрядов равны “1”. Только в этом случае значение i-го разряда изменится в следующей строке.

Однако, при движении по двоичной последовательности в обратном направлении (то есть снизу вверх) значение i-го разряда меняется тогда, когда текущие значения всех младших разрядов равны “0”.

Поскольку у триггеров имеется инверсный выход Q, то реализовать вы-

читающий счетчик довольно просто (рис. 4.3):

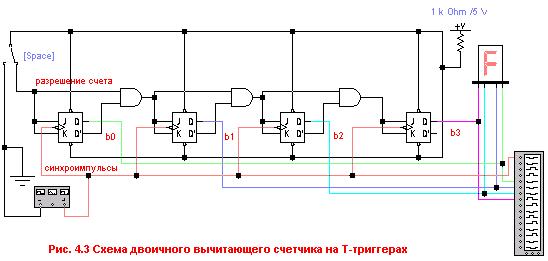
Приведенная схема является схемой синхронного двоичного вычитающего счетчика.

Изменить схему любого суммирующего счетчика, как синхронного, так и асинхронного на схему вычитающего счетчика можно переключением входов i+1 разряда на инверсные выходы триггеров i-го разряда. В результате получится вычитающий счетчик.

Выходы счетной последовательности всегда должны быть подключены к основным выходам триггеров (то есть к выходам Qi).

Рассмотренные нами счетчики являлись счетчиками по модулю «2», то есть число их возможных состояний было 2ⁿ.

Коэффициент пересчета.

Любой счетчик характеризуется числом состояний в течение одной счетной последовательности (цикла). Для схемы на рис. 4.1 цикл содержит N=2⁴=16 состояний (от 0000 до 1111). Часто число состояний называют коэффициентом пересчета К_СЧ, который равен отношению числа импульсов N_C на входе к числу импульсов N_Qст на выходе старшего разряда за цикл:

К_СЧ=N_С/N_Qст

Если на вход счетчика подавать периодическую последовательность импульсов с частотой f_С, то частота f_Q на выходе старшего разряда счетчика будет меньше в К_СЧ раз: К_СЧ=f_С/f_Q. Поэтому счетчики также называют делителями частоты, а величину К_СЧ – коэффициентом деления. Для увеличения величины К_СЧ приходится увеличивать число триггеров в цепочке. Каждый дополнительный триггер удваивает число состояний счетчика и число К_СЧ. Для уменьшения коэффициента К_СЧ можно в качестве выхода счетчика рассматривать выходы триггеров промежуточных каскадов. Например, для счетчика на четырех триггерах К_СЧ=16, если взять выход второго триггера, то К_СЧ=4. При этом К_СЧ является целой степенью числа 2: 2, 4, 8, 16 и т.д.

Можно реализовать счетчик, для которого К_СЧ – любое целое число. Например, для счетчика на трех триггерах можно сделать К_СЧ от 2 до 7, но при этом один или два триггера могут быть лишними. При использовании трех триггеров можно получить К_СЧ =5…7 (2² < К_СЧ < 2³). Счетчик с К_СЧ=5 должен иметь 5 состояний, которые в простейшем случае образуют последовательность: {0, 1, 2, 3, 4}. Циклическое повторение этой последовательности означает, что коэффициент деления счетчика равен 5.

Для построения суммирующего счетчика с К_СЧ=5 надо, чтобы после формирования последнего числа из последовательности {0, 1, 2, 3, 4} счетчик переходил не к числу 5, а к числу 0. В двоичном коде это означает, что от числа 100 нужно перейти к числу 000, а не к 101. Изменение естественного порядка счета возможно при введении дополнительных связей между триггерами счетчика.

Десятичные счетчики.

Десятичный счетчик состоит из нескольких подсчетчиков, соответствующих одному из десятичных разрядов. Такие подсчетчики называют декадными счетчиками(К_СЧ=10).

Счетная последовательность декадного счетчика зависит от способа представления десятичного числа. Наиболее распространено представление десятичных чисел в двоичном коде 8-4-2-1.

Этот код представляет каждую десятичную цифру четырехразрядным двоичным числом от 0000 до 1001. Очевидно, что счетная последовательность декадного счетчика должна предусматривать переход от двоичного кода 1001 (цифры 9 в десятичной системе счисления) к коду 0000 (поскольку цифры 10 в десятичной системе счисления нет).

Рассмотрим схему синхронного суммирующего декадного счетчика в коде 8-4-2-1 (рис. 4.4):

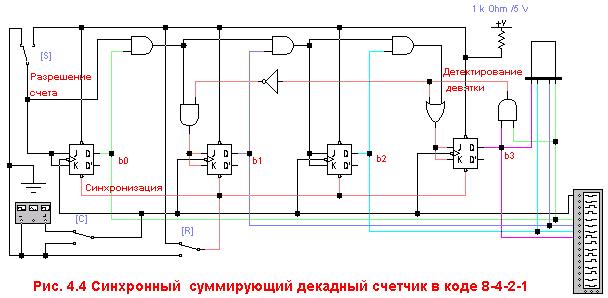
Эта схема представляет собой модификацию двоичного суммирующего счетчика, при которой счетная последовательность прерывается после девяти. Для этого в счетчике предусмотрена схема детектирования девятки.

Модификация двоичного суммирующего счетчика заключается в следующем:

1. Введем вентиль “И” с входами сигналов Q₀ и Q₃ (что соответствует коду 1001), имеющий на выходе логическую единицу только при этой кодовой комбинации.
2. Введем вентиль “ИЛИ” перед входом Т₃, обеспечивающий при кодовой комбинации 1001 на выходе декадного счетчика подачу логической единицы на вход ИЛИ и далее на вход Т₃, следовательно, следующий синхроимпульс установит выход b3 в логический нуль.
3. Введем инвертор “НЕ” и вентиль “И” перед входом Т₁, поэтому при кодовой комбинации 1001 на вход вентиля ”И” и далее на вход Т₁ триггера будет подан логический нуль, следовательно, следующий синхроимпульс не изменит состояние на выходе “b1” (т.е. “b1” останется в нулевом состоянии)
4. Состояние выходов “b0” и ”b2” не изменяется в связи с доработками, т.к. их значения и при нуле и при десяти равны логическому нулю(0000 и 1010).

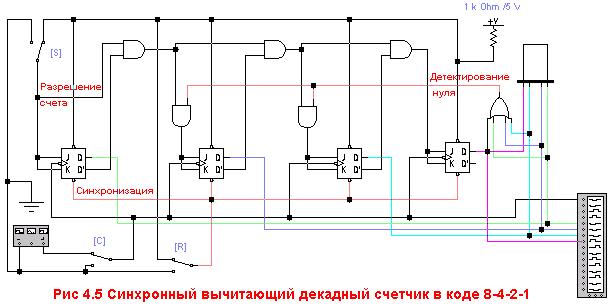
Аналогично можно построить схему синхронного вычитающего декадного счетчика в коде 8-4-2-1 (рис. 4.5):

N – разрядные счетчики.

Рассмотренные декадные счетчики служат основой для создания n -разрядных счетчиков по модулю 10, которые строятся по схемам, используемым при построении двоичных счетчиков.

Декада 1

Декада 2

Декада 3

В схемах n-разрядных счетчиков в каждой декаде сигнал “разрешение счета” должен быть равен единице тогда и только тогда, когда все предшествующие декады будут содержать девятки.

Таким же образом можно построить трехразрядный суммирующий счетчик в коде 4-2-1 по модулю 4 (рис. 4.6).

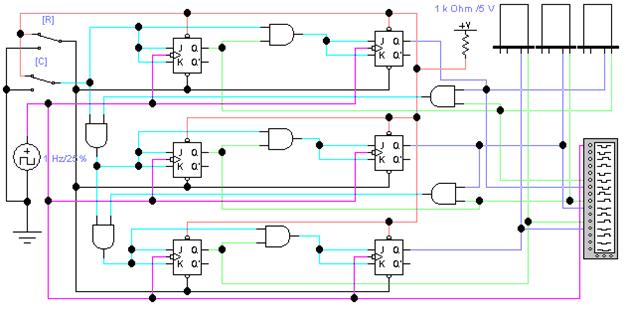
Рис. 4.6 Трехразрядный суммирующий счетчик в коде 4-2-1 по модулю 4.