Проектирование дешифраторов и шифраторов

Краткие сведения из теории:

Дешифраторы и шифраторы по существу принадлежат к числу преобразователей кодов. С понятием шифрации связано представление о сжатии данных, с понятием дешифрации - обратное преобразование.

Комбинационная схема, преобразующая поступающий на входы код в сигнал только на одном из ее выходов, называется дешифратором.

В условных обозначениях дешифраторов и шифраторов используются буквы DC и CD (от слов decoder и coder соответственно).

Дешифраторы:

Если количество двоичных разрядов дешифрируемого кода обозначить через n, то число выходов дешифратора должно быть 2ⁿ. С помощью n-разрядного двоичного кода можно отобразить 2ⁿ кодовых комбинаций, следовательно, число выходов полного дешифратора равно 2ⁿ. Таким образом, дешифратор содержит число выходов, равное числу комбинаций входных переменных, например: если число входов равно 3, то число выходов будет равно 2³=8.

Если часть входных наборов не используется, то дешифратор называют неполным и у него N_вых < 2ⁿ.

В ЭВМ с помощью дешифраторов осуществляется выборка необходимых ячеек запоминающих устройств, расшифровка кодов операций с выдачей соответствующих управляющих сигналов и т.д.

Если входные переменные представить как двоичную систему записи чисел, то логическая единица формируется в том выходе, номер которого соответствует десятичной записи того же числа. Например: A=1, B=0, C=0, D=1 соответствуют числу 1001 в двоичном коде. В десятичном коде это число 9, т.е. при данной комбинации входных переменных F₉ = 1. Дешифраторы широко используются в качестве преобразователей двоичного кода в десятичный код, а также во многих других устройствах.

Функционирование дешифратора описывается системой логических уравнений составленных на основе таблицы истинности.

Одноступенчатый (линейный) дешифратор - наиболее быстродействующий, но его реализация при значительной разрядности входного слова затруднена, поскольку требует применения логических элементов с большим числом входов и сопровождается большой нагрузкой на источники входных сигналов. Обычно одноступенчатыми выполняются дешифраторы на небольшое число входов (см. Рис. 1).

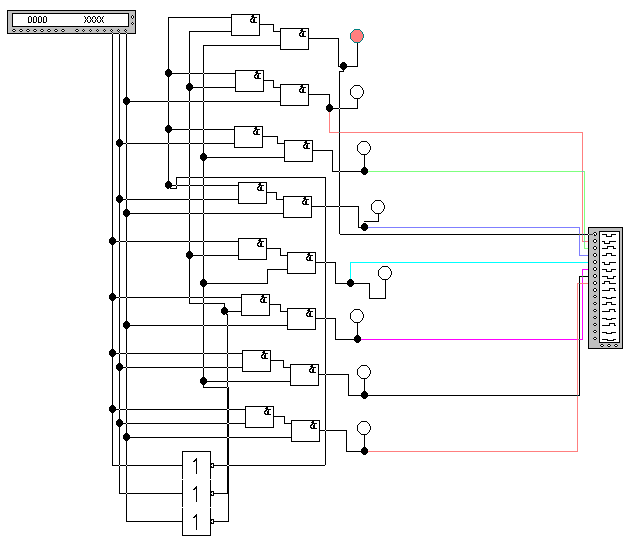
Рис. 1 - Схема дешифратора на 3 входа и 8 выходов

В приведенном на рисунке 1 примере дешифратор имеет 3 входа, следовательно, максимальное количество выходов будет равно 8. Построен дешифратор из простых логических элементов, с помощью таблицы истинности (см. таблицу 1) и составленных на основе этой таблицы логических уравнений.

	A	B	C	Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8

Таблица 1 - Таблица истинности

Уравнения для построения схемы:

1. Y1=A^ B^ C^;
2. Y5=A B^ C^;
3. Y2=A^ B^ C;
4. Y6=A B^ C;
5. Y3=A^ B C^;
6. Y7=A B C^;
7. Y4=A^ B C;
8. Y8=A B C.

На рисунке 2 приведена временная диаграмма работы дешифратора.

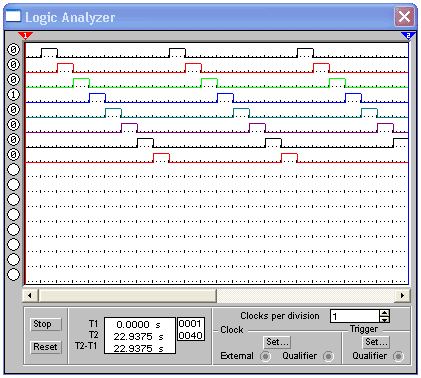
Рисунок 2 - Диаграмма работы дешифратора на 3 входа и 8 выходов

Матричные дешифраторы формируются на основе простых линейных дешифраторов меньшей размерности, т.е. строятся в виде матрицы.

Шифраторы:

Двоичные шифраторы преобразуют код “1из N” в двоичный код, т.е. выполняют операцию, обратную операции дешифраторов. При возбуждении одной из входных цепей шифратора на его выходах формируется слово, отображающее номер возбужденной цепи.

Полный двоичный шифратор имеет 2ⁿ входов и n выходов. Одно из основных применений шифратора - ввод данных с клавиатуры, при котором нажатие клавиши с десятичной цифрой должно приводить к передаче в устройство двоичного кода данной цифры. Пример построения шифратора показан на рисунке 3, а на рисунке 4 приведена временная диаграмма работы шифратора.

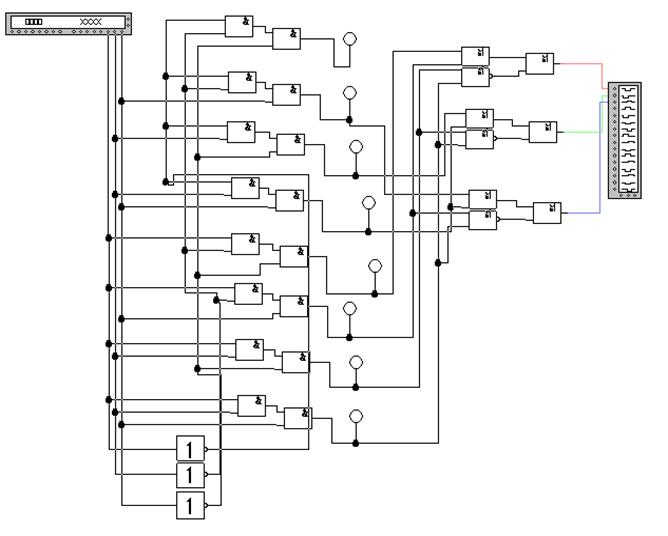
Рисунок 3 - Схема шифратора

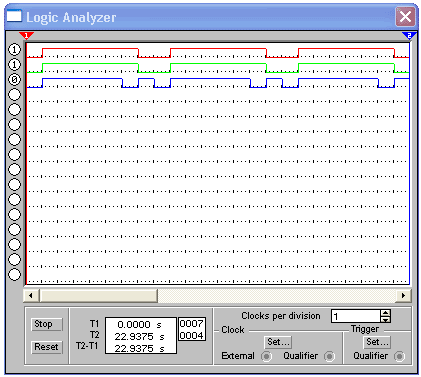
Рисунок 4- Диаграмма работы шифратора

Задание

1. Используя пакет Electronics Workbench спроектировать схемы, на основе простейших элементов используя для составления схемы таблицу истинности и логические уравнения. Проанализировать работу схемы с помощью логического анализатора.

2. Составить отчет о выполнении лабораторной работы в MS Word. В отчет включить: таблицу истинности и логические уравнения, схему дешифратора или шифратора, временные диаграммы работы схемы.

Варианты заданий:

1. Построить DC и CD с n =2.

2. Построить DC с n =3, используя элементы 2И и НЕ.

3. Построить DC с n =3, используя элементы 3И и НЕ.

4. Построить DC с n =4, используя элементы 2И и НЕ.

5. Построить DC с n =4, используя элементы 2И, 3И и НЕ.

6. Построить DC с n =4, используя элементы 4И и НЕ.

7. Построить DC с n =4, используя DC с n=2.

8. Построить DC с n =4, используя DC с n=3.

9. Построить CD для преобразования десятичной цифры из В=10 в В=2.

10. Построить клавиатурный CD с n =3, используя элементы 2ИЛИ.

11. Построить клавиатурный CD с n =3, используя элементы 4ИЛИ.

12. Построить клавиатурный CD с n =4.

13. Построить клавиатурный CD для ввода десятичных цифр.

14. Построить CD для вывода десятичной цифры, представленной в В=2, используя элементы 4ИЛИ и НЕ.

СЧЕТЧИКИ.

Цель работы: