Построение простейших логических схем
Г.В. ПОТЕХИН
ЛАБОРАТОРНЫЕ РАБОТЫ
По курсу
"ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА"
(2 курс, 4 семестр)
Утверждено
на заседании кафедры 605
протокол № 2 от 11октября 2007г.
Доказательство основных тождеств
Булевой алгебры
Для выполнения работы необходимо использовать опыт лабораторной работы №1.
Для доказательства тождества необходимо построить схемы-аналоги логических уравнений обоих частей тождества и проанализировать выходные параметры каждой схемы.
Тождество будем считать доказанным, если временные диаграммы выходных параметров правой и левой части уравнения будут совпадать.
Тождества алгебры логики представлены в таблице ниже:
| № | Логическое выражение | Формулировка |
| F1=X*0=0 | Логическое произведение любого аргумента на 0 равно 0 | |
| F2=X*1=X | Логическое произведение любого аргумента на 1 равно значению аргумента | |
| F3=X*X=X | Логическое произведение одних и тех же аргументов равно аргументу | |
| F4=X*X^=0 | Логическое произведение аргумента с его инверсией равно 0 | |
| F5=X+0=X | Логическая сумма любого аргумента с 0 равна аргументу | |
| F6=X+1=1 | Логическая сумма любого аргумента с 1 равна 1 | |
| F7=X+X=X | Логическая сумма аргумента с самим собой равна аргументу | |
| F8=X+X^=1 | Логическая сумма аргумента с его инверсией равна 1 | |
| F9=X^^=Х | Двойная инверсия аргумента дает его истинное значение | |
| F10=X1*X2=X2*X1 | Переместительный закон | |
| F11=X1+X2=X2+X1 | -“- | |
| F12=(X1*X2)*X3=X1*(X2*X3) | Сочетательный закон | |
| F13=(X1+X2)+X3=X1+(X2+X3) | -“- | |
| F14=X1*(X2+X3)=X1*X2+X1*X3 | Раскрытие скобок | |
| F15=X1+(X2*X3)=(X1+X2)*(X1+X3) | Исключенное третье | |
| F16=X1+X1*X2=X1 | Поглощение | |
| F17=X1+X1^*X2=X1+X2 | -“- | |
| F18=(X1*X2)^=X1^+X2^ | 1 правило де Моргана | |
| F19=(X1+X2)^=X1^*X2^ | 2 правило де Моргана |
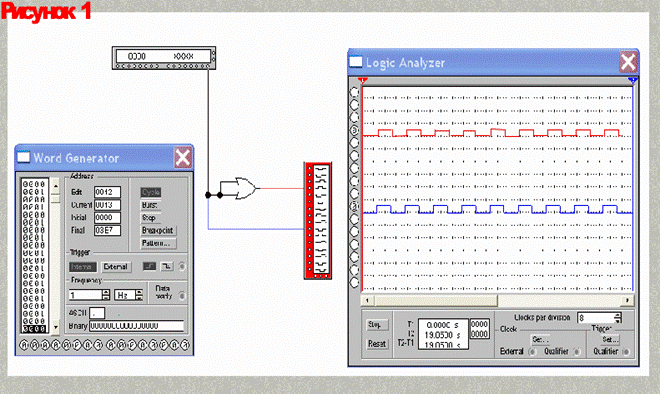
В качестве примера рассмотрим седьмое тождество из таблицы.
На рис. 1 приведены схемы для обеих частей тождества и временная диаграмма входных и выходных характеристик для схемы.
ЗАДАНИЕ
1. Используя пакет Electronics Workbench спроектировать схемы, соответствующие обеим частям тождества, и с помощью проведения анализа доказать тождество.
2. Составить отчет о выполнении лабораторной работы в MS Word. В отчет включить построенные схемы для обеих частей тождества и диаграммы входных и выходных сигналов каждой из выполненных схем, а также вывод, полученный в результате сравнения выходных сигналов для каждой схемы.
3. Лабораторная работа выполняется в соответствии с вариантами заданий, полученными у преподавателя (см. таблицу ниже).
| № ВАРИАНТА | НОМЕРА ТОЖДЕСТВ | ||
| Т1 | Т10 | Т19 | |
| Т2 | Т11 | Т18 | |
| Т3 | Т12 | Т17 | |
| Т4 | Т13 | Т16 | |
| Т5 | Т14 | Т15 | |
| Т6 | Т15 | Т14 | |
| Т7 | Т16 | Т13 | |
| Т8 | Т17 | Т12 | |
| Т9 | Т18 | Т11 | |
| Т5 | Т10 | Т19 | |
| Т1 | Т9 | Т11 | |
| Т2 | Т8 | Т12 | |
| Т3 | Т7 | Т13 | |
| Т4 | Т6 | Т14 | |
| Т5 | Т12 | Т15 | |
| Т6 | Т4 | Т16 | |
| Т7 | Т3 | Т17 | |
| Т8 | Т2 | Т18 | |
| Т9 | Т1 | Т19 |
Рис. 1 - Схема дешифратора на 3 входа и 8 выходов
В приведенном на рисунке 1 примере дешифратор имеет 3 входа, следовательно, максимальное количество выходов будет равно 8. Построен дешифратор из простых логических элементов, с помощью таблицы истинности (см. таблицу 1) и составленных на основе этой таблицы логических уравнений.
| A | B | C | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 | Y8 | |
Таблица 1 - Таблица истинности
Уравнения для построения схемы:
- Y1=A^ B^ C^;
- Y5=A B^ C^;
- Y2=A^ B^ C;
- Y6=A B^ C;
- Y3=A^ B C^;
- Y7=A B C^;
- Y4=A^ B C;
- Y8=A B C.
На рисунке 2 приведена временная диаграмма работы дешифратора.
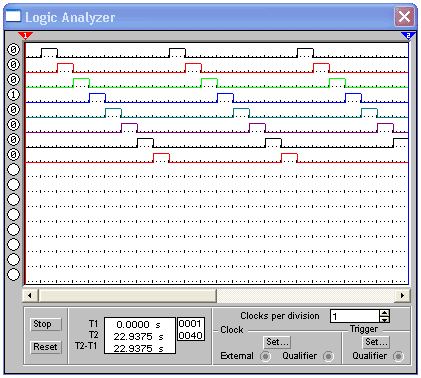
Рисунок 2 - Диаграмма работы дешифратора на 3 входа и 8 выходов
Матричные дешифраторы формируются на основе простых линейных дешифраторов меньшей размерности, т.е. строятся в виде матрицы.
Шифраторы:
Двоичные шифраторы преобразуют код “1из N” в двоичный код, т.е. выполняют операцию, обратную операции дешифраторов. При возбуждении одной из входных цепей шифратора на его выходах формируется слово, отображающее номер возбужденной цепи.
Полный двоичный шифратор имеет 2n входов и n выходов. Одно из основных применений шифратора - ввод данных с клавиатуры, при котором нажатие клавиши с десятичной цифрой должно приводить к передаче в устройство двоичного кода данной цифры. Пример построения шифратора показан на рисунке 3, а на рисунке 4 приведена временная диаграмма работы шифратора.
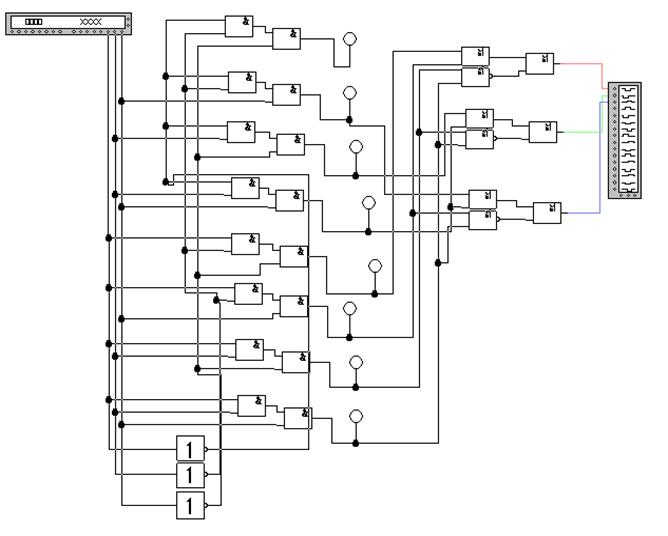
Рисунок 3 - Схема шифратора
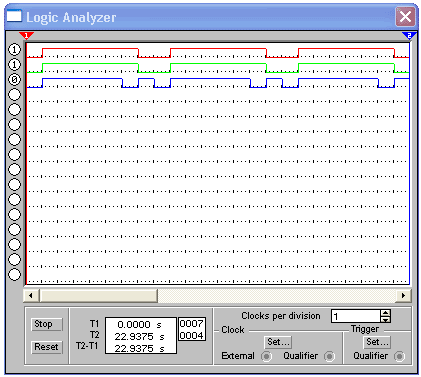
Рисунок 4- Диаграмма работы шифратора
Задание
1. Используя пакет Electronics Workbench спроектировать схемы, на основе простейших элементов используя для составления схемы таблицу истинности и логические уравнения. Проанализировать работу схемы с помощью логического анализатора.
2. Составить отчет о выполнении лабораторной работы в MS Word. В отчет включить: таблицу истинности и логические уравнения, схему дешифратора или шифратора, временные диаграммы работы схемы.
Варианты заданий:
1. Построить DC и CD с n =2.
2. Построить DC с n =3, используя элементы 2И и НЕ.
3. Построить DC с n =3, используя элементы 3И и НЕ.
4. Построить DC с n =4, используя элементы 2И и НЕ.
5. Построить DC с n =4, используя элементы 2И, 3И и НЕ.
6. Построить DC с n =4, используя элементы 4И и НЕ.
7. Построить DC с n =4, используя DC с n=2.
8. Построить DC с n =4, используя DC с n=3.
9. Построить CD для преобразования десятичной цифры из В=10 в В=2.
10. Построить клавиатурный CD с n =3, используя элементы 2ИЛИ.
11. Построить клавиатурный CD с n =3, используя элементы 4ИЛИ.
12. Построить клавиатурный CD с n =4.
13. Построить клавиатурный CD для ввода десятичных цифр.
14. Построить CD для вывода десятичной цифры, представленной в В=2, используя элементы 4ИЛИ и НЕ.
СЧЕТЧИКИ.
 |
Цель работы:
Electronics Workbench
Microsoft Word
Приборы и элементы:
В Electronics Workbench используются:
1.  Семисегментный индикатор (панель «Indicators»):
Семисегментный индикатор (панель «Indicators»): 
2.  Источник напряжения +5В (панель «Basic»)
Источник напряжения +5В (панель «Basic») 
3. 
 Коннекторы, двухпозиционные переключатели (панель «Basic»)
Коннекторы, двухпозиционные переключатели (панель «Basic») 
4.  Логические элементы (панель «Logic Gates»)
Логические элементы (панель «Logic Gates») 
5. 


 JK-триггер, D-триггер (панель «Digital»)
JK-триггер, D-триггер (панель «Digital»)
6. 
 Шина заземления, генератор синхроимпульсов (панель «Sources»)
Шина заземления, генератор синхроимпульсов (панель «Sources»)

7. 
 Генератор сигналов, логический анализатор (панель «Instruments»)
Генератор сигналов, логический анализатор (панель «Instruments»)

Краткие сведения из теории:

Счетчик- это последовательностная схема, на основе регистра, которая в
соответствии с импульсами на счетной линии проходит через предписанную
последовательность состояний - счетную последовательность.
Счетная последовательность может циклически повторяться, тогда мы имеем циклический счетчик.
Счетная последовательность может завершаться некоторым, предварительно обусловленным, состоянием, в этом случае счетчик называют
счетчиком с насыщением.
Двоичные счетчики.
Двоичный счетчик - это совокупность триггеров, т.е. регистр, каждый триггер которого ассоциируется с битами в двоичном представлении числа.
В том случае, когда счетная последовательность начинается с ”0”, а заканчивается максимальным значением (2n-1), счетчик называют суммирующим.
В противном случае, т.е. когда счетная последовательность начинается с максимального значения (2n-1) и оканчивается “О”, счетчик называют вычитающим
Коэффициент пересчета.
Любой счетчик характеризуется числом состояний в течение одной счетной последовательности (цикла). Для схемы на рис. 4.1 цикл содержит N=24=16 состояний (от 0000 до 1111). Часто число состояний называют коэффициентом пересчета КСЧ, который равен отношению числа импульсов NC на входе к числу импульсов NQст на выходе старшего разряда за цикл:
КСЧ=NС/NQст
Если на вход счетчика подавать периодическую последовательность импульсов с частотой fС, то частота fQ на выходе старшего разряда счетчика будет меньше в КСЧ раз: КСЧ=fС/fQ. Поэтому счетчики также называют делителями частоты, а величину КСЧ – коэффициентом деления. Для увеличения величины КСЧ приходится увеличивать число триггеров в цепочке. Каждый дополнительный триггер удваивает число состояний счетчика и число КСЧ. Для уменьшения коэффициента КСЧ можно в качестве выхода счетчика рассматривать выходы триггеров промежуточных каскадов. Например, для счетчика на четырех триггерах КСЧ=16, если взять выход второго триггера, то КСЧ=4. При этом КСЧ является целой степенью числа 2: 2, 4, 8, 16 и т.д.
Можно реализовать счетчик, для которого КСЧ – любое целое число. Например, для счетчика на трех триггерах можно сделать КСЧ от 2 до 7, но при этом один или два триггера могут быть лишними. При использовании трех триггеров можно получить КСЧ =5…7 (22 < КСЧ < 23). Счетчик с КСЧ=5 должен иметь 5 состояний, которые в простейшем случае образуют последовательность: {0, 1, 2, 3, 4}. Циклическое повторение этой последовательности означает, что коэффициент деления счетчика равен 5.
Для построения суммирующего счетчика с КСЧ=5 надо, чтобы после формирования последнего числа из последовательности {0, 1, 2, 3, 4} счетчик переходил не к числу 5, а к числу 0. В двоичном коде это означает, что от числа 100 нужно перейти к числу 000, а не к 101. Изменение естественного порядка счета возможно при введении дополнительных связей между триггерами счетчика.
Десятичные счетчики.
Десятичный счетчик состоит из нескольких подсчетчиков, соответствующих одному из десятичных разрядов. Такие подсчетчики называют декадными счетчиками(КСЧ=10).
Счетная последовательность декадного счетчика зависит от способа представления десятичного числа. Наиболее распространено представление десятичных чисел в двоичном коде 8-4-2-1.
Этот код представляет каждую десятичную цифру четырехразрядным двоичным числом от 0000 до 1001. Очевидно, что счетная последовательность декадного счетчика должна предусматривать переход от двоичного кода 1001 (цифры 9 в десятичной системе счисления) к коду 0000 (поскольку цифры 10 в десятичной системе счисления нет).
Рассмотрим схему синхронного суммирующего декадного счетчика в коде 8-4-2-1 (рис. 4.4):
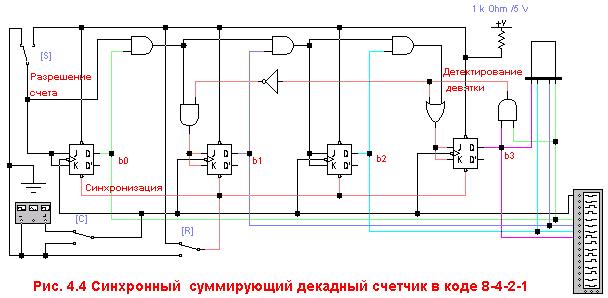
Эта схема представляет собой модификацию двоичного суммирующего счетчика, при которой счетная последовательность прерывается после девяти. Для этого в счетчике предусмотрена схема детектирования девятки.
Модификация двоичного суммирующего счетчика заключается в следующем:
- Введем вентиль “И” с входами сигналов Q0 и Q3 (что соответствует коду 1001), имеющий на выходе логическую единицу только при этой кодовой комбинации.
- Введем вентиль “ИЛИ” перед входом Т3, обеспечивающий при кодовой комбинации 1001 на выходе декадного счетчика подачу логической единицы на вход ИЛИ и далее на вход Т3, следовательно, следующий синхроимпульс установит выход b3 в логический нуль.
- Введем инвертор “НЕ” и вентиль “И” перед входом Т1, поэтому при кодовой комбинации 1001 на вход вентиля ”И” и далее на вход Т1 триггера будет подан логический нуль, следовательно, следующий синхроимпульс не изменит состояние на выходе “b1” (т.е. “b1” останется в нулевом состоянии)
- Состояние выходов “b0” и ”b2” не изменяется в связи с доработками, т.к. их значения и при нуле и при десяти равны логическому нулю(0000 и 1010).
Аналогично можно построить схему синхронного вычитающего декадного счетчика в коде 8-4-2-1 (рис. 4.5):
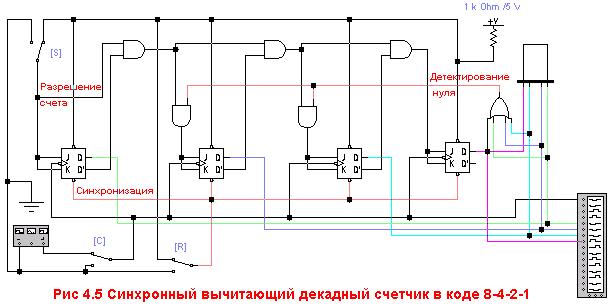
N – разрядные счетчики.
Рассмотренные декадные счетчики служат основой для создания n -разрядных счетчиков по модулю 10, которые строятся по схемам, используемым при построении двоичных счетчиков.
 | |||
 | |||
 | |||


















|
|
|
 |
В схемах n-разрядных счетчиков в каждой декаде сигнал “разрешение счета” должен быть равен единице тогда и только тогда, когда все предшествующие декады будут содержать девятки.
Таким же образом можно построить трехразрядный суммирующий счетчик в коде 4-2-1 по модулю 4 (рис. 4.6).
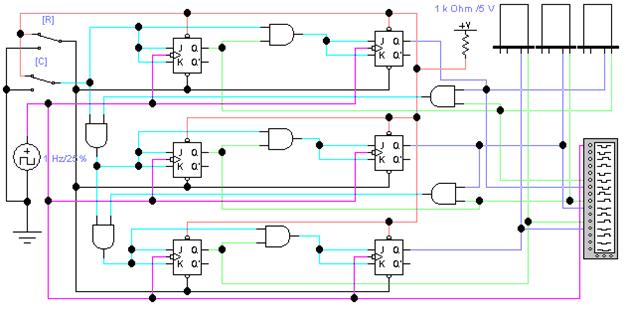
Рис. 4.6 Трехразрядный суммирующий счетчик в коде 4-2-1 по модулю 4.
Г.В. ПОТЕХИН
ЛАБОРАТОРНЫЕ РАБОТЫ
По курсу
"ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА"
(2 курс, 4 семестр)
Утверждено
на заседании кафедры 605
протокол № 2 от 11октября 2007г.
Построение простейших логических схем
в программеElectronicsWorkbench
Краткие теоретические сведения:
Все устройства ЭВМ состоят из элементарных логических схем. Работа этих схем основана на законах и правилах алгебры логики, которая оперирует двумя понятиями: истинности и ложности высказывания. В соответствии с такой двоичной природой высказываний условились называть их логическими двоичными переменными и обозначать 1 в случае истинности и 0 в случае ложности. Примерами логических переменных являются высказывания:
A = “Земля плоская”, B = “Автомобиль имеет двигатель”
На основании этих высказываний можно записать: A = 0; B = 1, так как высказывание A – ложно, а высказывание B истинно.
Высказывания могут быть простыми и сложными: простые содержат одно законченное утверждение, сложные образуются из двух или большего числа простых высказываний, связанных между собой некоторыми логическими связями. Формализация и преобразование связей между логическими переменными осуществляется в соответствии с правилами алгебры логики называемой алгеброй Буля.
Две логические переменные A и B, принимающие значение 0 или 1, могут образовывать логические функции. В алгебре логики любые функции удобно изображать в виде таблицы соответствия всех возможный комбинаций входных логических переменных и выходной логической функции, называемой таблицей истинности.
Ниже приведен полный перечень функций двух аргументов. Функции, образованные логическими переменными, можно преобразовывать в соответствии с правилами или законами алгебры логики. При этом стремятся минимизировать логическое выражение, т.е. привести его к виду, удобному для практической реализации на логических элементах (см. таблицу 1).
| Функция | Название функции | Х1 | ||||
| Х2 | ||||||
| F1= x1 /\ x2 | Конъюнкция – логическое умножение (И) | |||||
| F2= x1 \/ x2 | Дизъюнкция – логическое сложение | |||||
| F3= x1 → x2 | Импликация х1 в х2 | |||||
| F4= х1 ← х2 | Импликация х2 в х1 | |||||
| F5=x1 Þ x2 | Запрет х2 | |||||
| F6=x1 Ü x2 | Запрет х1 | |||||
| F7=x1 ~ x2 | Эквивалентность | |||||
| F8=x1 Å x2 | Сложение по модулю 2 | |||||
| F9=x1/x2 | И-НЕ – Штрих Шеффера | |||||
| F10=x1 ↓ x2 | ИЛИ-НЕ – Стрелка Пирса | |||||
| F11=x1 | Повторение х1 | |||||
| F12=x2 | Повторение х2 | |||||
| F13=1 | Константа 1 | |||||
| F14=0 | Константа 0 | |||||
| F15=x1^ | Инверсия х1- НЕ х1 | |||||
| F16=x2^ | Инверсия х2- НЕ х2 |
Таблица 1 - Таблица Истинности
Проектирование схем вElectronicsWorkbench:
Пакет Electronics Workbench предназначен для моделирования и анализа электротехнических и схемотехнических схем. Данный пакет с большой степенью точности моделирует построение реальных схем в "железе". Electronics Workbench является приложением под операционные системы Windows 95/98/NT/2000/XP.
Запуск Electroncis Workbench:
Пакет Electronics Workbench запускается как любое другое приложение с помощью меню Пуск или иконки на Рабочем столе:

Горизонтальное меню:
File - организация работы с файлами. С помощью этого раздела меню пользователь осуществляет работу с файлами (открытие, создание, распечатку файлов и прочее).
Edit - с помощью этого раздела пользователь осуществляет редактирование и работу с текущим документом. Опции раздела позволяют копировать, удалять, перемещать элементы или блоки схемы. Кроме того возможна настройка визуальных параметров схемы (расположение и ориентация элементов схемы, настройка цветов и шрифта, поиск и другие стандартные функции).
Circuit - раздел, позволяющий вращать, менять свойства, приближать и отдалять элементы схемы.
Analysis - раздел служит для проведения различного рода анализов схем.
Window - раздел предназначен для выполнения экранных настроек при работе с документами.
Help - раздел служит для доступа к справочной системе Electronics Workbench.
При проектировании схем в Electronics Workbench используются элементы панели компонентов Logic Gates: Or, Nor, And, Nand, Xor, Xnor, Inverters, на необходимое число входов.
Все виды анализа осуществляются с помощью элементов панели инструментов "Instruments" (см. рисунок 1).

Рисунок 1 - Панель инструментов
Приборы
Multimeter. Используйте этот прибор для измерения переменного или постоянного напряжения или тока, или сопротивления или потери децибел между двумя точками в схеме. Multimeter автоматически выставляет диапазоны измерений, поэтому Вам не нужно самим указывать диапазон измерений. Внутренние сопротивление и ток предустановленны и имеют значения близкие к идеальным. Эти значения могут быть изменены при помощи нажатия на кнопку "Settings".
Oscilloscope. Двухканальный осциллограф отображает амплитуду и колебания электронных сигналов. Данный прибор способен отображать интенсивность одного или двух сигналов во времени или же сравнивать одну временную диаграмму с другой.
Bode plotter. Графопостроитель Боде рисует график частоты ответов схемы, и он полезен для анализа схем фильтрации. Данный прибор используется для
измерения увеличения напряжения сигнала или сдвига фазы. Когда графопостроитель Боде подключен к схеме, выполняется спектральный анализ.
Logic Analyzer. Анализатор логики отображает уровни до 16 цифровых сигналов. Он используется для быстрого сбора данных о логическом состоянии проектируемой схемы.
Для имитации работы спроектированной цифровой схемы её входы подключаются к генератору тактовых импульсов. Он также выбирается из панели компонентов Instruments и называется Word Generator.
Программирование цифрового генератора:
Генератор имеет 16 выходов. Для программирования логических сигналов на выходах генератора требуется прописывать картину нулей и единиц на каждую итерацию генератора путём непосредственного ввода двоичного кода или шестнадцатеричных кодов ASCII (см. рисунок 2).
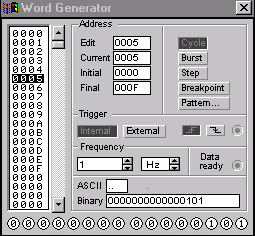
Рисунок 2 – Окно настройки цифрового генератора
Для визуального отображения состояния выходов генератора можно собрать схему, содержащую цифровой генератор, семисегментный цифровой индикатор с дешифратором и четыре логических индикатора.
Программируем генератор двоичными значениями шестнадцатеричных цифр. В процессе работы схема будет отображать все шестнадцатеричные цифры на цифровом индикаторе (см. рисунок 3).
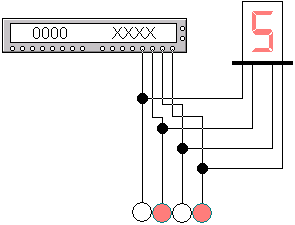
Рисунок 3 – Пример схемы с цифровым генератором и индикатором
Рассмотрим пример построения схемы и оформления лабораторной работы:
Задана функция F2(А, В) - Дизъюнкция:
Логическое сложение двух переменных A и B есть логическая функция F2, которая истинна тогда, когда истинна одна из двух входных переменных. F2 = A+B. Для функции логического сложения таблица истинности имеет вид:
| А | ||||
| В | ||||
| F |
Таблица 2 - Дизъюнкция - логическое сложение
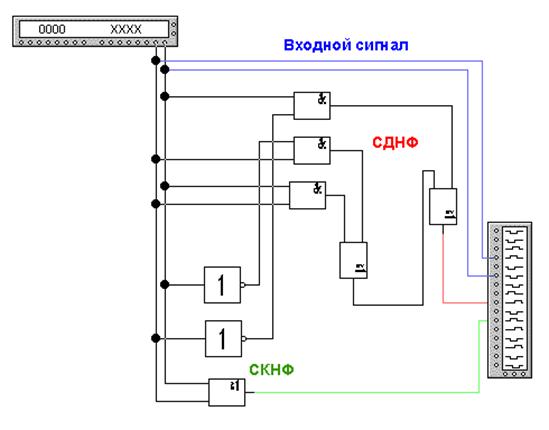
Рисунок 4 - Графическая схема функции сложения
Функция F2=A+B. Графическая схема проектирования функции сложения,созданная в программе Electronics Workbench приведена на рисунке 4
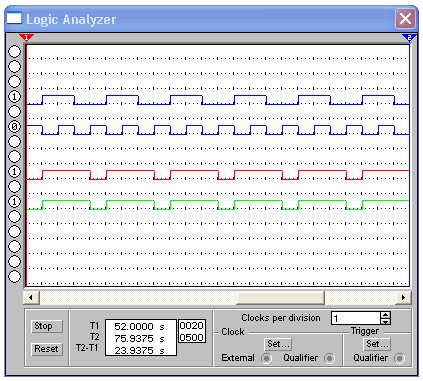
Рисунок 5 - Диаграммы входных и выходных сигналов
После приведения самой схемы нарисованной и собранной в программе Electronics Workbench вы должны привести диаграммы входных и выходных сигналов (см. рисунок 5).
Для проверки можно сравнить диаграммы входных и выходных сигналов с таблицей истинности. Как видно на 1-ом такте A=1; B=0; F2=1. Сравним это с таблицей истинности и увидим, что Fn совпадают. При полном совпадении выходной функции на других тактах и при другом сочетании переменных можно сделать вывод, что построенная схема работает правильно. На этом описание этой функции заканчивается. Другие функции описываются и собираются аналогично.
При построении и проектировании других лабораторных работ проверка работоспособности построенной схемы выполняется также. Проверяются диаграммы входных и выходных сигналов и сравниваются по тактам с таблицей истинности.
Задание:
1. Используя пакет Electronics Workbench спроектировать схемы логических функций;
2. Составить отчет о выполнении лабораторной работы в MS Word. В отчет включить построенные схемы и диаграммы входных и выходных сигналов каждой из выполненных схем;
3. Лабораторная работа выполняется в соответствии с вариантами (см. таблицу 3).
| N варианта | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 | F16 |
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + | ||||||||||||||
| + | + | + |
Таблица 3 - Варианты заданий
