Решение задач на тему: логические схемы

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ ПО ДИСЦИПЛИНЕ «ЭЛЕМЕНТЫ И УСТРОЙСТВА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ»

для студентов очной формы обучения специальности

230106 «Техническое обслуживание средств

вычислительной техники и компьютерных сетей»

Орел 2009 г.

ОДОБРЕНА Кафедрой «Вычислительной техники и информационных технологий»     Зав. кафедрой   ______________________ Р.Н. Яковлев   «______» ____________________ 2009 г.

Составлена в соответствии с Государственными требованиями к минимуму содержания и уровню подготовки выпускника по специальности   Зам. декана ФСПО по УР   ____________________ С.Р. Бондарева   «______» ____________________ 2009 г.

Автор: В.В. Покровский, преподаватель кафедры «Вычислительной техники и информационных технологий» ФСПО ТИ ОрелГТУ

Содержание

ВВЕДЕНИЕ

Основная трудность в изложении элементов цифровой техники состоит в существенном разрыве между уровнем знаний школьников и современным состоянием ЭВТ. Учащимся необходимо преодолеть дистанцию огромного размера – от двоичной арифметики и простейших логических элементов до архитектуры микропроцессора и ЭВМ. Многообразие элементной базы, ее миниатюризация, отсутствие наглядности, необходимость использования различных кодов, синтез многополюсников требуют от учащихся высокого уровня абстрактного мышления. Изучение базовых логических элементов, элементов памяти, операционных элементов и их комбинаций и последовательную логику на физическом уровне становится невозможным из-за громоздкости и отсутствия наглядности. Они рассматриваются схемотехнически: зависимость между входными и выходными сигналами описывается таблицами истинности или функциями на языке алгебры логики.

Практикум включает следующие темы:

· Основы алгебры логики.

· Решение задач на тему «Логические схемы».

· Виртуальный логический конвертор.

· Цифровой компаратор.

· Устройство контроля четности.

· Мультиплексоры и демультиплексоры.

· Арифметические сумматоры.

· Виртуальный генератор слова.

· Виртуальный логический анализатор.

· Триггеры.

· Счетчик.

· Регистр.

· Оперативное запоминающее устройство.

Выполнение этих работ позволит учащимся более глубоко понимать процессы, происходящие в работе электронных вычислительных машин.

ФИЗИЧЕСКИЕ ОСНОВЫ ЭВМ

Основные понятия и законы алгебры логики

Науку о человеческом мышлении создал древнегреческий ученый Аристотель (384-322 г. до н. э.). Он назвал ее логикой. Логика предписывала общие правила, по которым человек должен мыслить, делать умозаключение и приходить к истине. Немецкий математик, Г.В. Лейбниц (1646-1716 гг.) сблизил логику с вычислениями. У него возникла мысль создать новую науку — математическую логику, в которой логические понятия обозначены математическими знаками. Только почти через 200 лет английский математик, Джордж Буль (1815-1864 гг.) частично реализовал идеи Лейбница. Он создал для логических обоснований и рассуждений необычную алгебру, в которой логические высказывания обозначались особыми символами подобно тому, как в школьной алгебре числа обозначаются буквами. Оказалось что, оперируя этими символами и логическими связками, можно выполнять логические рассуждения при помощи обычных вычислений.

Исследования показали, что в человеческой речи чаще всего встречаются повествовательные предложения, излагающие что-нибудь или описывающие какие-нибудь события. Эти предложения являются высказываниями. В Булевой алгебре высказывания рассматриваются не по содержанию и не по смыслу, а только в отношении того истинно оно или ложно. Принято обозначать: истинно — 1, а ложно — 0. Приведем примеры логических высказываний: «снег холодный». Данное предложение является высказыванием и при том истинным. «Снег теплый» — высказывание, но ложно. «Речка движется и не движется» не является высказыванием, так как из этого предложения нельзя понять истинно оно или ложно. «Который час?» — это не высказывание, а вопросительная фраза. Буль показал, что простейшее высказывание, связанное между собой союзами: «И», «ИЛИ», «НЕ» — составляют составное высказывание, истинность или ложность, которого можно вычислить.

Конъюнкция — Λ (логическое умножение), Λ, Χ, &, «и», and.

Дизъюнкция — V (логическое сложение), V, +, «или», or.

Отрицание — ⌐, «не», −, not.

Логическое «исключающее или», .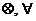

Импликация – , -.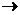

Двойная импликация или эквиваленция – .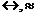

Таблицы истинности:

A	B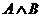

A	B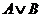

A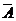

A	B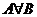

A	B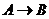

A	B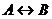

Логическое исключающее ИЛИ, импликацию и эквиваленцию можно выразить через три основных логических операций: конъюнкцию, дизъюнкция, отрицание.

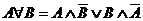
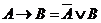
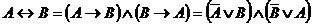
Основные формулы алгебры логики:

Законы коммутативности:

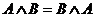
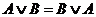
Законы ассоциативности:

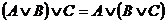
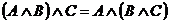
Законы идемпотентности:

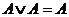
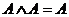
Законы дистрибутивности:

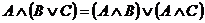
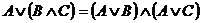
Формулы позволяющие упрощать логические выражения:

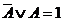
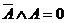
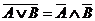
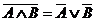
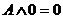
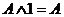
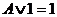
Приоритет выполнения логических операций. Сначала выполняются операции расположенные в скобках. При отсутствии скобок, первой выполняется операция отрицания, если она относится к одной логической операции, затем конъюнкция, а потом дизъюнкция.

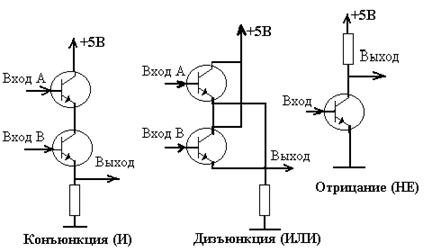
Физические основы ЭВМ

Рис. 1

Выше приведены (рис. 1.) реализации элементов булевой алгебры на базе транзисторов. Промышленность выпускает сотни типов электронно-логических элементов. В интегральном исполнении представляющих собой сочетание элементов «И», « ИЛИ», «НЕ». В виде примера рассмотрим один из самых распространенных типов логических микросхем типа K155LA3 (рис. 2), представляющее собой сочетание в одном корпусе четырех двухходовых схем «И» — «НЕ». Каждая логическая схема «И», «НЕ» имеет два входа (выводы 1 и 2, 4 и 5, 9 и 10, 12 и 13) и один выход (выводы 3,. 6, 8, 11).

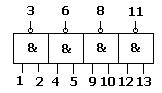
Рис. 2.

Таблица истинности приведенной выше микросхемы.

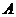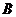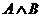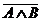Принятые обозначения логических элементов в электрических схемах приведены на рис. 3.

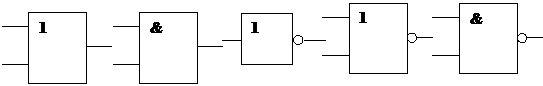Рис. 3

Логическое сложение (дизъюнкция) - ИЛИ, логическое умножение (конъюнкция) - И, отрицание - НЕ, логический элемент «2-ИЛИ – НЕ», логический элемент «2-И – НЕ». Обозначения логических операций: * - конъюнкция, + - дизъюнкция, ‘ (апостроф) – отрицание.

Содержание занятия

· Задача 1. Проведите анализ логического устройства (рис. 4): по функциональной схеме составьте структурную формулу, упростите ее, если это возможно.

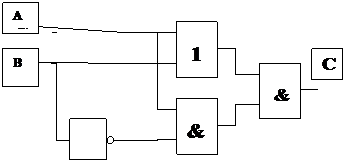
Рис. 4

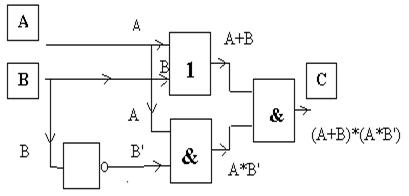
Рис. 5

Решение. 1. Составление логической функции для функциональной (логической) схемы. При составлении логической функции необходимо проследить пути движения потоков сигналов (рис. 5).

Ответ: (А+В)*( А*В’).

2. Проверка на избыточность функциональной схемы (упростить логическую функцию, т. е. преобразовать с помощью законов алгебры логики).

(А+В) *(А* В’) =/ Скобки для А*В’ опускаем, так как перед скобками тоже знак * / =(А+В)*А*В’= / Для А*В’ применяем закон коммутативности / =(А+В)*В’*А= / Для (А+В)*В’ применяем закон дистрибутивности/ = ((А*В’)+(В*В’))*А= / В*В’=0/ = ((А*В’)+0)*А=/ Поглощение 0 при дизъюнкции/ =(А*В’)*А=/ Скобки опускаем , применяем закон коммутативности/=А*А*В’=/ А*А=А/=А*В’.

3. Проверяем справедливость логических преобразований. Для этого составляем таблицу истинности. В общем случае составляем две таблицы: для исходной и конечной логических функций. В данной задаче достаточно одной. Значения таблиц истинности А*В’ и (А+В)*(А*В’) равны, что доказывает справедливость логических преобразований.

А	В	А+В	В’	А*В’	(А+В)*(А*В’)

1. По полученной логической функции составляем функциональную схему (рис.6).

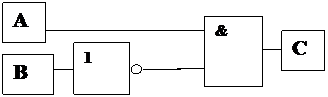Рис. 6

Задача 2.Провидите синтез трехвходового логического устройства с выходной комбинацией 00110010 в таблице истинности.

Решение. 1. Составим таблицу истинности для данного логического устройства.

А	В	С	F(A,B,C)
				A’*B*C’=1
				A’*B*C=1
				A*B*C’=1

Так как в таблице F единиц меньше чем нулей, то построим СДНФ: (A’*B*C’)+(A’*B*C)+(A*B*C’).

2. Используя правила алгебры логики попробуем его упростить.

(A’*B*C’)+(A’*B*C)+(A*B*C’)= [((A’*B)*C’)+((A’*B)*C)]+(A*B*C’)=

=[(A’*B)*(C’+C)]+(A*B*C’)= / C’+C=1/ =[(A’*B)*1]+(A*B*C’)=

=(A’*B)+(A*B*C’)= (A’*B)+((A*C’)*B)= (A’+(A*C’))*B=B*(A’+A*C).

Упрощаем дальше, используя закон де Моргана.

B*(A’+A*C’)=B*(A’’*(A*C’)’)’= B*(A*(A’+C’’))’= B*(A*(A’+C))’=

=B*((A*A’)+(A*C))’=/A*A’=0, 0+(A*C)=A*C/=B*(A*C)’=B*(A’+C’)=

= B*A’+B*C’.(Проверку можно осуществить с помощью таблиц истинности).

Ответ: B*A’+B*C’.

3. По полученной структурной формуле построим функциональную схему (рис.7).

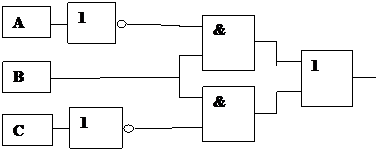Рис. 7

Краткая теория

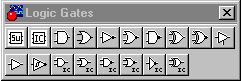
Рис. 9

Теперь для решения предложенных выше задач воспользуемся программой электронной лаборатории Electronics Workbench. Для построения логических схем в библиотеке Logic Gates (логические элементы) предусмотрено возможность выбора логических элементов. На рис. 9 перечень выбора возможных логических элементов.

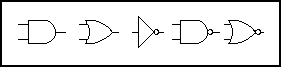
Рис. 10.

На рис. 10 показаны обозначения, используемые в Electronics Workbench логических элементов: конъюнкции - И, дизъюнкции – или, отрицания –НЕ, 2 – И – НЕ, 2 –ИЛИ – НЕ.

В электронной лаборатории Electronics Workbench имеется виртуальное устройство. Логический конвертор (Logic Converter) позволяет осуществлять 6 логических преобразований для логической функции с числом переменных от 1 до 8: представление таблицы истинности собранной из логических элементов схемы; обращение таблицы истинности в логическую формулу (СДНФ); минимизацию СДНФ; обращение формулы в таблицу истинности; представление формулы в виде схемы в логическом базисе 2-И-НЕ. Логический конвертор выбирается из меню Instruments (рис. 11).

Рис. 11

Приведем описание технологии исследования логических схем с помощью логического конвертора (преобразователя).

1. Собираем логическую схему.

2. Подключаем исследуемую логическую схему к логическому конвертору (входов 8, выход один – расположен справа).

3. Открываем логический конвертор щелчком левой кнопкой мыши по иконке конвертора. На экране появляется меню Logic Converter (рис. 12).

4. Для получения таблицы истинности нажимаем

5. Для получения логической функции (структурной формулы) нажимаем

С помощью логического конвертора можно проводить не только анализ логических устройств, но их синтез.

Приведем описание технологии синтеза логического устройства по выходной комбинации с помощью логического конвертора (преобразователя).

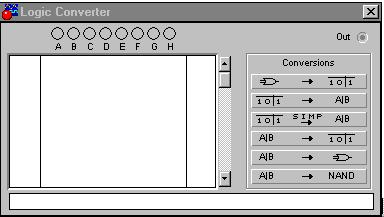
Рис. 12

Раскрываем лицевую панель логического конвертора (рис. 12).

1. Активизируем курсором клеммы-кнопки A, B, ..H (начиная с F), количество которых равно количеству входов синтезируемого устройства (количеству логических переменных).

2. Вносим необходимые изменения в столбец OUT и после нажатия на клавиши на панели преобразователя получаем результат в виде схемы на рабочем поле программы и логическую функцию в дополнительном дисплее.

Задача 3. Проведите анализ логического устройства (рис. 13) по функциональной схеме с помощью Electronics Workbench.

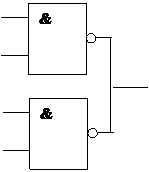
Рис. 13

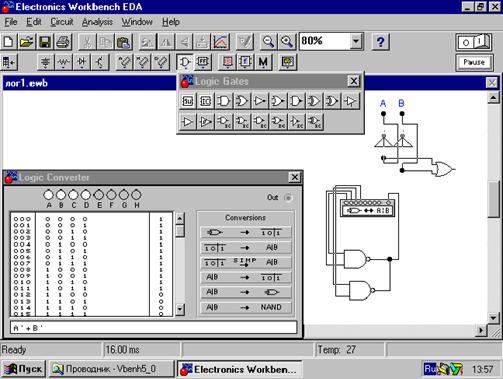
На рис. 14 решение задачи в Electronics Workbench.

Контрольные вопросы и задания

1. Объяснить назначение и принцип работы логического конвертора. Решить следующие задания с использованием логического конвертора.

2. Исследуйте следующие функциональные схемы.

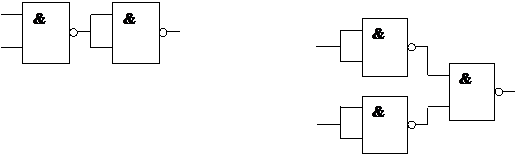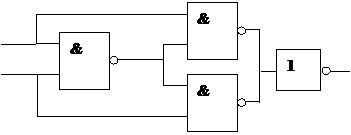3. Исследуйте логическую схему и постройте функциональную логическую схему:

а) B*C’+A*C.

б) A*B’C+A*B’*C’+A’*B’*C.

с) A*(B+C)*(D+C).

4.Провидите синтез логического устройства с выходной комбинацией:

а) 00100111.

б) 01101001.

с) 0110100110010110.

Краткая теория

Цифровые компараторы (от английского compare – сравнивать) выполняют сравнение двух чисел А, В одинаковой разрядности, заданных в двоичном или двоично-десятичном коде. В зависимости от схемного исполнения компараторы могут определять равенство А=В или неравенства А<B,A>B. Результат сравнения отображается в виде логического сигнала на одноименных выходах, в случае выполнения условия на выходе 1.

Цифровые компараторы применяются для выявления нужного числа (слова) в цифровых последовательностях, для выполнения условных переходах.

Схемы одноразрядных компараторов приведены на рис. 15, 16, 17..

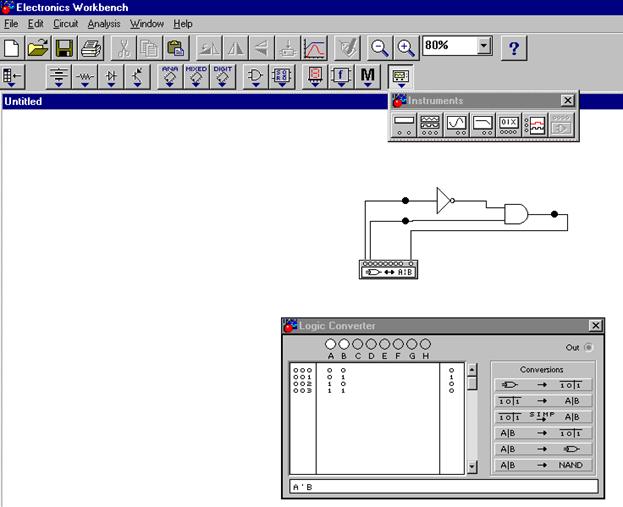
Рис. 15

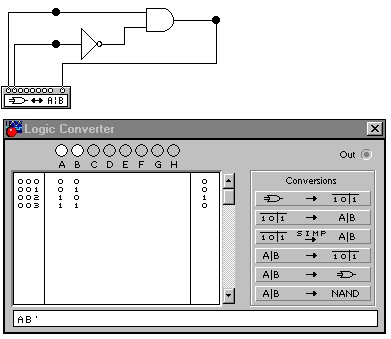
Рис. 16

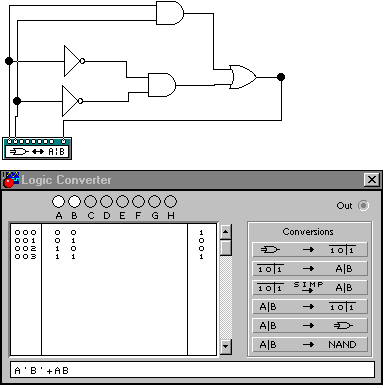
Рис. 17

Операциям сравнения (A<B, A=B, A>B) соответствуют структурные формулы (A’*B, A’*B’+A*B, A*B’).

Условно обозначим логические схемы компараторов:

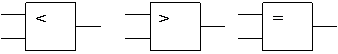Тогда, компараторы =>, <=, <> будут выглядеть следующим образом:

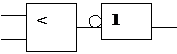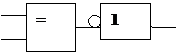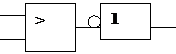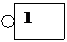где элемент отрицания.

Логические функции этих компараторов выглядят:

(A’*B)’, (A*B’)’, (A’*B’+A*B)’.

Можем упростить данные формулы с помощью законов алгебры логики:

(A’*B)’=A’’+B’=(закон де Моргана)=A+B’ (закон двойного отрицания),

(A*B’)’=A’+B’’=A’+B,

(A’*B’+A*B)’=(A’’+B’’)*(A’+B’)=(A+B)*(A’+B’).

Таблицы истинности для данных формул:

A	B	B’	A+B’ (A=>B)	A’	A’+B (A<=B)	A+B	A’+B’	(A+B)*(A’+B’) (A<>B)

Контрольные вопросы и задания

1. Какие функции выполняет цифровой компаратор, в каких устройствах он может быть использован?

2. Подсоединив схемы к логическому конвектору, исследуйте приведенные схемы.

3. Составьте схему устройства, объединяющую все три компаратора.

4. Составьте схемы устройств, удовлетворяющие условиям: A<=B, A<>B, A>=B.

5. Исследуйте составленные схемы устройств.

6.Составьте структурные формулы и таблицы истинности для составленных выше логических схем цифровых компараторов.

Краткая теория

Операция контроля четности двоичных чисел позволяет повысить надежность передачи и обработки информации. Ее сущность заключается в суммировании по модулю 2 всех разрядов с целью выяснения четности числа, что позволяет выявить наиболее вероятную ошибку в одном из разрядов двоичной последовательности. Например, если при передаче кода 1001 произойдет сбой во втором разряде, то на приемном пункте получим код 1101 – такую ошибку определить в общем случае затруднительно. Если же код относится к двоично-десятичному (способ кодирования десятичных чисел, при котором каждая цифра представляется четырьмя двоичными разрядами – двоичной тетрадой), обнаружение ошибок путем введения дополнительного бита четности происходит следующим образом. На передающей стороне передаваемый код анализируется и дополняется контрольным битом до четного или нечетного числа единиц в суммарном коде. Соответственно суммарный код называется четным или нечетным. В случае нечетного кода дополнительный бит формируется таким образом, чтобы сумма всех единиц в передаваемом коде, включая контрольный бит, была нечетной. При контроле четности все наоборот. Например, в числе 0111 число единиц нечетно. Поэтому при контроле нечетности дополнительный код должен быть нулем, а при контроле четности – единицей. На практике чаще всего используется контроль нечетности, поскольку он позволяет фиксировать полное пропадание информации (случай нулевого кода во всех информационных разрядах). На приемной стороне производится проверка кода четности. Если он правильный, то прием разрешается, в противном случае включается сигнализация ошибки или посылается передатчику запрос на повторную передачу.

Схема формирования бита четности для четырехразрядного кода приведена на рис.18

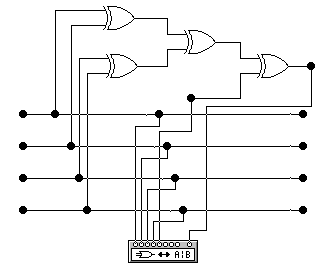
Рис. 18.

Она содержит четыре элемента исключающие ИЛИ, выполняющие функции сумматоров по модулю 2 (без переноса) и состоит из трех ступеней. На первой ступени попарно суммируются все биты исходного кода на входах A, B, C, D. На второй ступени анализируются сигналы первой ступени, и устанавливается четность или нечетность суммы входного кода. На третьей ступени полученный результат сравнивается с контрольным сигналом на входе E, задающим вид используемого контроля, в результате чего на выходе F формируется дополнительный пятый бит четности, сопровождающий информационный сигнал в канале передачи.

Результаты моделирования приведены на рис. 19.

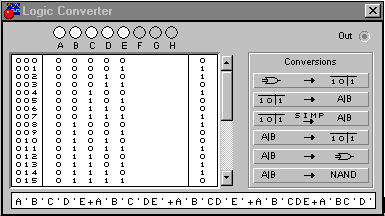
Рис. 19

Контрольные вопросы и задания

1. Какое назначение имеют формирователи кода четности, где они могут быть использованы?

2. Постройте схему формирователя бита четности трехразрядного (пятиразрядного) кода.

3. Проанализируйте работу составленных схем формирователей битов четности.

Краткая теория

Назначение мультиплексоров (от английского multiplex – многократный) – коммутировать в заданном порядке сигналы, поступающие с нескольких входных шин в одну выходную. У мультиплексора может быть, например, 16 входов и один выход. Это означает, что если к этим входам присоединить 16 источников цифровых сигналов – генераторов последовательных цифровых слов, то байты от любого из них можно передавать на единственный выход. Для выбора любого из 16 каналов необходимо иметь 4 входа селекции (2⁴=16), на которые подается двоичный адрес канала. Так, для передачи данных от канала номер 9 на входах селекции необходимо установить код 1001. В силу этого мультиплексоры часто называют селекторами или селекторами-мультиплексорами.

На рис. 20 приведена схема двухканального мультиплексора, состоящего из элементов ИЛИ, НЕ и двух элементов И.

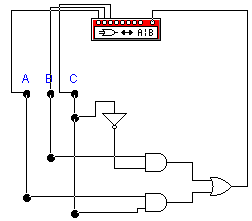
Рис. 20. Схема двухканального мультиплексора

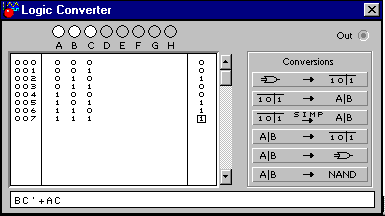
Рис. 21

Результаты моделирования двухканального мультиплексора с помощью логического конвертора показаны на рис. 21, из которого видно, что его выходной сигнал описывается структурной формулой B*C’+A*C, т.е. сигнал из канала А проходит на выход при адресном входе С=1, а из канала В - при С=0, что и соответсвует логике работы мульти плексора.

Демультиплексоры в функциональном отношении противоположны мультиплексорам. С их помощью сигналы с одного информационного входа распределяются в требуемой последовательности по нескольким выходам. Выбор нужной выходной шины, как и в мультиплексоре, обеспечивается установкой соответствующего кода на адресных входах. При m адресных входах демультиплексор может иметь до 2^m выходов.

Принцип работы демультиплексора поясним с помощью схемы на рис. 22.

Y0   Y1

А     Х

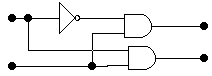
Рис. 22. Схема демультиплексора

Схема содержит два элемента элемента И и один элемент НЕ. На схеме: Х - информационный вход, А - вход адреса, Y0, Y1 - выходы.

Если А=0 сигнал информационного входа передается на выход Y0, а при A=1 - на выход Y1.

Контрольные вопросы и задания

1. Что такое мультиплексор, каково его назначение?

2. Что такое демультиплексор, для решения каких задач его можно применить?

3. Придумайте схему трехканального мультиплексора?

4. Придумайте схему трехвыходного демультиплексора?

Краткая теория

С помощью логических схем можно выполнять арифметические операции с двоичными числами.

Двоичная таблица сложения всего четырьмя формулами:

A	B	A+B

При сложении двоичных чисел в каждом разряде образуется сумма и при этом возможен перенос в старший разряд. Введем обозначения слагаемых (A, B), переноса (P), и суммы (S). Тогда таблица сложения одноразрядных двоичных чисел с учетом переноса в старший разряд выглядит следующим образом:

Слагаемые	Перенос	Сумма
A	B	Р	S
				A’+B’
					A’*B
					A*B’
				A+B

Отсюда видно, что перенос P=A*B, для СКНФ S=(A’+B’)*(A+B);

для СДНФ S=A’*B+A*B’.

Логические схемы с входами A,B и выходами P, S для соответствующих формул:

P

S

B

A

A

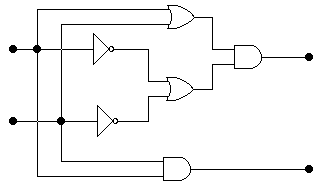Рис. 23

P

S

B

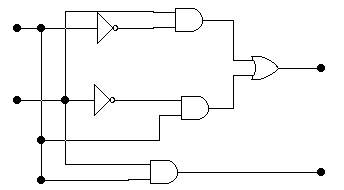Рис. 24

Преобразуем формулу S=(A’+B’)*(A+B), используя, закон де Моргана: S=(A*B)’*(A+B).

Логическая схема для данной формулы (рис. 25):

P

S

B

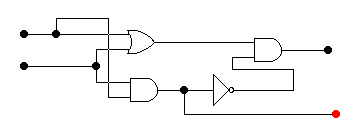Рис. 25

Как видим, что для реализации арифметического устройства сложения достаточно четырех логических элементов.

Приведенные логические устройства называются полусумматорами.

Полный одноразрядный сумматор должен иметь три входа: A, B - слагаемые и P₀ - перенос из младшего разряда и два выхода сумму S и перенос P.

Слагаемые	Перенос из младшего разряда	Перенос	Сумма
A	B	P0	Р	S

Формула переноса (СДНФ): P=(A*B)+(A*P₀)+(B*P₀). Для получения суммы необходимо результат логического сложения переменных A, B,P₀ умножить на P’:

S=(A+B+P₀)*P’.

Данное логическое выражение дает правильное значение во всех случаях, кроме, когда все входные переменные принимают логическую 1.

P=(A*B)+(A*P₀)+(B*P₀)+(A*B*P₀) - данная формула дает ожидаемый результат.

Арифметические сумматоры являются составной частью так называемых арифметико-логических устройств (АЛУ) микропроцессоров. В программе EWB арифметические сумматоры представлены в библиотеке Digital двумя базовыми устройствами: полусумматорами и полными сумматорами. Они имеют следующие назначения выводов: А, В – входы слагаемых, S - результат суммирования, С₀ – выход переноса, С_i - вход переноса. N – разрядный сумматор создается на базе одного полусумматора и n-1 полных сумматоров. На рис.26 приведено исследование полусумматора.

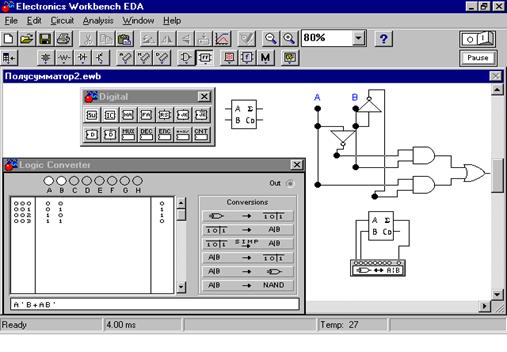
Рис. 26

На рис.27 приведена схема подключения полного сумматора к логическому конвертору и трехразрядный сумматор.

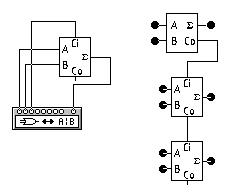
Рис. 27

Контрольные вопросы и задания

1. Чем отличается полусумматор от полного сумматора.

2. Выясните внутреннюю структуру полного сумматора, пользуясь схемой подключения к логическому конвертору, аналогично приведенному анализу полусумматора.

3. Исследуйте выходы переноса полусумматоров и полного сумматора.

4. Исследуйте приведенный трехразрядный сумматор, последовательно подключая выходы к логическому конвертору.

Краткая теория

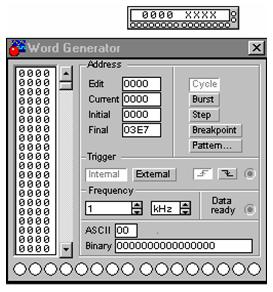
Рис. 28

Внешний вид виртуального генератора слова и лицевая панель приведены на рис. 28.

Генератор (его еще кодовым генератором) предназначен для генерации 16 разрядных двоичных слов. Кодовые комбинации необходимо задавать в шестнадцатиричном коде.

Каждая комбинация заносится с помощью клавиатуры, номер редактируемой ячейки фиксируется в окошке EDIT блока ADRESS. Всего таких ячеек и следовательно, комбинаций – 2048. В процессе работы генератора в отсеке ADRESS индицируется номер текущей ячейки (CURRENT), ячейки инициализации или начала работы (INITIAL) и конечной ячейки (FINAL). Выдаваемые на 16 выходов (В нижней части генератора) кодовые комбинации индицируются в текстовом (ASCII) и двоичном коде (BINARY).

Сформированные слова выдаются на 16 расположенных в нижней части виртуального прибора клемм-индикаторов:

· В пошаговом (при нажатии кнопки STEP), циклическом (при нажатии кнопки CYCLE) или с выбранного слова до конца (при нажатии клавиши BURST) при заданной частоте посылок (установка – нажатиями кнопок в окнах FREQUENCY);

· При внутреннем (при нажатии кнопки INTERNAL) или внешнем запуске (при нажатии кнопки EXTERNAL по готовности данных (клемма DATA READY), рядом расположена клемма для подключения канала синхронизации);

· При запуске по переднему или заднему фронту.

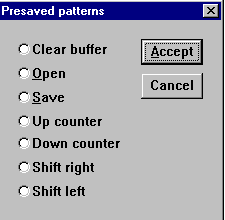
Рис. 29

На клемму CLK выдается выходной синхронизирующий импульс. К органам управления относится также кнопка BREAK POINT – прерывание работы генератора в указанной ячейке. При нажатии на кнопку PATTERN выпадает меню (рис. 29), где:

- Clear buffer – стереть содержимое буфера (содержимое буфера экрана);

- Open – загрузить кодовые комбинации (из файла с расширением .dp);

- Save – записать все набранные на экране комбинации в файл (.dp);

- Up counter - заполнить буфер экрана кодовыми комбинациями, начиная с 0 в нулевой ячейке и далее с прибавлением 1 в каждой последующей ячейке;

- Down counter – заполнить буфер кодовыми комбинациями, начиная с FFFF в нулевой ячейке и далее с уменьшением на 1 в каждой последующей ячейке;

- Shift right – заполнить каждые четыре ячейки комбинациями 1-2-4-8 со смещением их в следующих четырех ячейках вправо;

- Shift left – тоже самое, но со смещением влево.

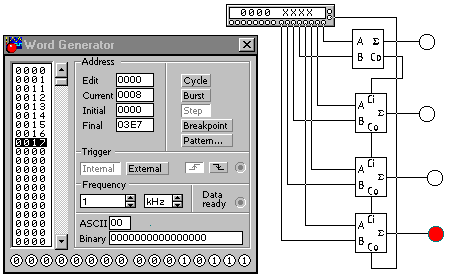
Рис. 30

Задание. Исследовать четырех разрядный сумматор (рис. 30) с помощью виртуального генератора слов.

1. Собираем четырех разрядный сумматор, состоящий из одного полусумматора и трех полных сумматоров.

2. Из панели Indicators выбираем 4 индикатора и подключаем к выходам сумматора (при сигнале 1 – зажигаются).

3. Выходы виртуального генератора слов подключаем к входам сумматора; четыре первых разряда соответствуют первому слагаемому, четыре последующих разряда – второму слагаемому.

4. В лицевой панели генератора вводим шестнадцатиразрядные числа 0, 1, 11, 12, 13, 14, 15, 16, 17.

5. Запустить генератор слов в режиме Step. Проанализировать работу сумматора.

Вычитание

Вычитание числа В из А выполняется путем суммирования отрицательного числа В в дополнительном коде с числом А. Представление отрицательного двоичного числа можно получить путем инвертирования всех битов числа и добавлением 1. Прибавление этой единицы эффективно реализуется в полном сумматоре путем замены его первого каскада (полусумматора) на полный сумматор, вход переноса которого подключается к напряжению с уровнем логической 1.

Контрольные вопросы и задания

1. Объяснить предназначение виртуального генератора слов.

2. Перечислить основные функции генератора слов.

3. Объяснить, почему выбраны шестнадцатиразрядные числа 0, 1, 11, 12, 13, 14, 15, 16, 17 для анализа работы сумматора.

4. Постройте пятиразрядный сумматор и проанализируйте с помощью генератора слов.

5. Какие шестнадцатиразрядные числа необходимо ввести для анализа работы сумматора?

6. Как обеспечить вычитание двух чисел?

Лабораторная работа № 7. Виртуальный логический анализатор. (Logic Analyzer)

Цель: Изучение назначения и принцип работы устройства логического анализатора. Знакомство с базовыми функциями логического анализатора.

Оборудование: Электронная лаборатория Electronics Workbench.

Краткая теория

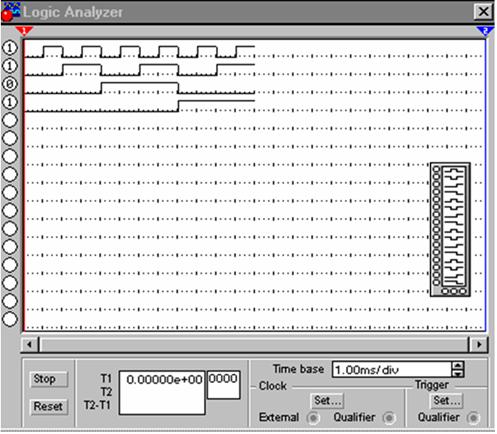
Рис. 31

Внешний вид виртуального логического анализатора приведен на рис. 31.

Анализатор предназначен для отображения на экране монитора 16-разрядных кодовых последовательностей одновременно в 16 точках схемы, а также в виде двоичных чисел на входных клеммах-индикаторах. Длительность развертки задается в окне TIME BASE. В блоке Clock имеются клеммы как для обычного (Extend), так и избирательного (Qualifier) источника запускающих сигналов, параметры которых могут установлены с помощью меню, вызываемого кнопкой Set (рис. 32). Запуск генератора можно осуществлять по переднему (Pozitive) или заднему (Negative) фронту запускающего сигнала с использованием внешнего (External) или внутреннего (Internal) источника. В окне Clock qualifier можно установить значение логического сигнала (0, 1 или Х), при котором производится запуск анализатора.

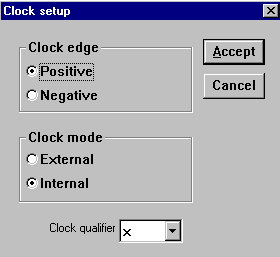
Рис. 32

Дополнительные условия запуска анализатора могут быть выбраны с помощью меню, которое вызывается кнопкой Set в блоке Trigger (рис. 33). C помощью этого окна в каналах А, В и С можно задать нужные двоичные 16-разрядные комбинации сигналов и затем в строке Trigger combinations установить дополнительные условия отбора:

- A OR B – запуск анализатора от канала А или В;

- A THEN B – запуск анализатора от канала А, если сигнал в канале В равен 1;

- (A OR B)THEN C – запуск анализатора от канала А или В, если сигнал в канале С равен 1.

В окне канала Trigger qualifier можно задать логические сигналы 1, 0 или Х, при наличии которых производится запуск анализатора.

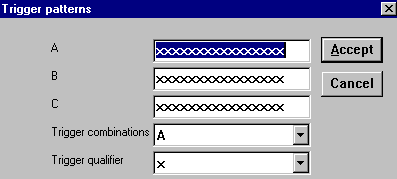
Рис. 33

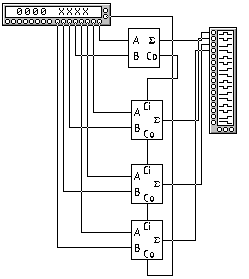
Рис. 34

Задание. Изучение четырех разрядного сумматора (рис. 34) с помощью логического анализатора.

Контрольные вопросы и задания

1. Описать принцип работы логического анализатора.

2. Для чего предназначен логический анализатор.

3. Выполнить следующее задание.

Краткая теория

Любая информация в компьют