СНКФ для выше приведенной таблицы истинности будут иметь вид
.
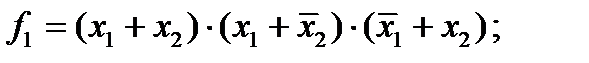
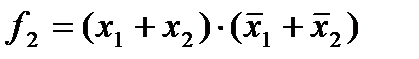2)
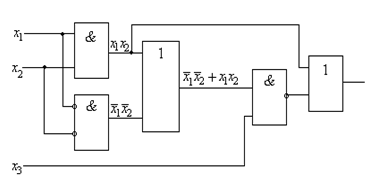
Билет 12.
1) приведем правила минимизации с помощью КК. Пример
1. 
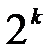соседних клеток, содержащих 1, и расположенных по вертикали либо по горизонтали в виде прямоугольника либо квадрата (такую совокупность клеток называют покрытием), соответствуют одной импликанте, ранг которой 
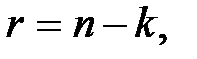где 
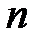− число переменных, меньше ранга покрываемых конституентна 
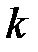единиц. Чем больше клеток в покрытии, тем проще выражаемый этим покрытием член логической функции − импликанта.
2. Импликанта, соответствующая некоторому покрытию заполненных единицами клеток, содержит символы тех переменных, значения которых совпадают у всех клеток, образующих покрытие. Причем символ берется с отрицанием, если для всех клеток покрытия он принимает значение 0, и без отрицания – в противном случае.
Каждое покрытие нужно использовать только один раз. Если КК свернуть в цилиндр вдоль горизонтальной или вертикальной оси, то будет видно, что крайние клетки тоже оказываются соседними и они могут образовывать покрытие.
2) Хз
Билет 20
1) Логическая функция [функция алгебры логики (ФАЛ)]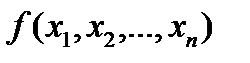 
– это выражение, представляющее собой сложное высказывание, состоящее из нескольких простых высказываний 
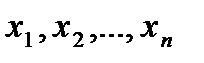,связанных соединительными словами. Это сложное высказывание принимает значения 0 или 1 на всех наборах логических значений всех простых высказываний.
Определение 1. Формула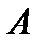 
, принимающая истинное значение при любых комбинациях значений входящих в нее высказываний, называется тождественно истинной (ТИФ) или тавтологией и записывается 
.
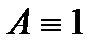Определение 2. Формула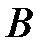 
, принимающая ложное значение при любых комбинациях значений входящих в нее высказываний, называются тождественно ложной (ТЛФ) и записывается 
.
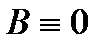Например: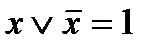 
- ТИФ, 
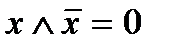- ТЛФ.
Определение 3. Две формулы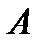 
и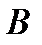 
алгебры логики называются равносильными, если они принимают одинаковые логические значения при всех комбинациях логических значений входящих в них высказываний. Равносильность, как и тождественность, обозначают знаком “ 
” 
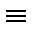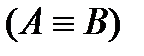
Например, построив таблицу истинности для высказывани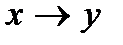й 
и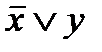 
можно убедиться, что они являются равносильными формулами (т.е. столбцы для первой и второй формул будут одинаковыми), т.е. 
.
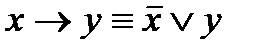2) получится провод
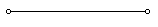
Билет 6
1) Логическую сумму двух элементарных конъюнкций разных рангов, из которых одна является частью другой, можно заменить слагаемым, имеющим меньший ранг.
Пример: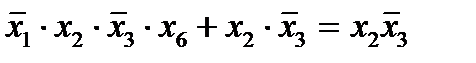 
Правило поглощения для элементарных дизъюнкций формулируется следующим образом: логическое произведение двух элементарных дизъюнкций разных рангов, одна из которых является частью другой, можно заменить сомножителем меньшего ранга.
Пример: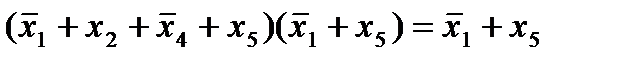 
.
2) Ложны
Билет 11
1) шаги в каждом методе могут иметь свою особенность.
1.Склеивание всевозможных членов исходной СНКФ, т.е. сначала конституент, затем импликант ранга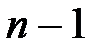 
и т.д., пока склеивание возможно.
2. Проверка каждой простой импликанты в сНКФ на избыточность с целью её удаления. Проверка состоит в следующем. Так как любая импликанта равна 0 для НКФ лишь на одном наборе переменных, то если на этом наборе сумма остальных членов также обращается в (0), то рассматриваемая импликанта не влияет на значение истинности данной логической функции, т.е. она является избыточной. Удаляя все такие импликанты, получим ТНКФ.
3. Упрощение полученной ТНКФ путем применения операции отрицания и распределительного закона 1-го или 2-го рода.
2) 
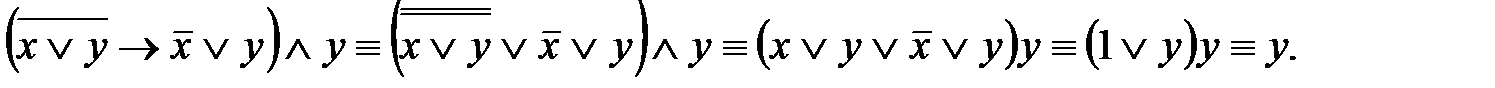
Билет 7
1) Закон двойственности.
Пусть формула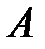 
содержит только операции конъюнкции, дизъюнкции и отрицания. Операцию конъюнкции называют двойственной операции дизъюнкции, и наоборот.
Определение. Формулы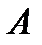 
и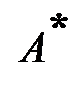 
называются двойственными, если формула 
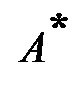получена из формулы 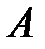путем замены в ней каждой операции на двойственную. Например: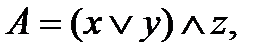 
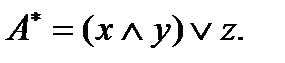
2) 1) при b, равном 1 – ложно. 2) всегда, при любых b - ложно 3) при b=1 – истинно
Билет 4
1) Сначала введем некоторые понятия. Логическое произведение 
сумма любого числа высказываний называется элементарным, если сомножители слагаемые в нем являются либо одиночными высказываниями, либо их отрицаниями.
Например: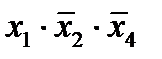 
– элементарное произведение,
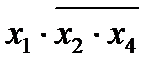– неэлементарное произведение.
Количество сомножителей в элементарном произведении называется его рангом.
Два элементарных произведения одинакового ранга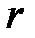 
называются соседними, если они являются формулами одних и тех же высказываний и отличаются знаком отрицания только одного высказывания.
Теперь сформулируем само правило склеивания для элементарных конъюнкций: логическую сумму двух соседних произведений некоторого ранга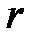 
можно заменить одним элементарным произведением ранга 
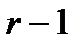, являющимся общей частью исходных слагаемых.
Пример: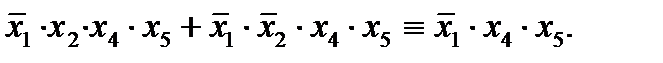 
Аналогично для дизъюнкции определяются ранг и соседство. Правило склеивания для элементарных дизъюнкций формулируется следующим образом: логическое произведение двух соседних дизъюнкций ранга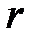 
можно заменить одной дизъюнкцией ранга 
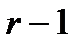, являющейся общей частью исходных сомножителей.
Пример: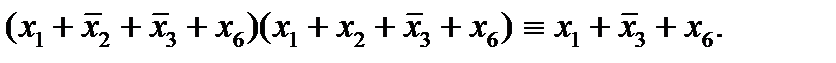 
2) ХЗ
Билет 18
1) 1. В развертываемую элементарную конъюнкцию ранга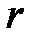 
вводятся в качестве дополнительных сомножителей 
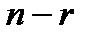единиц, где 
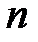– число высказываний и 
.
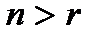2. Каждая единица представляется в ви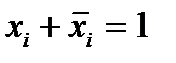де 
, где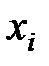 
– высказывание, отсутствующее в исходной конъюнкции.
3. Производится раскрытие всех скобок на основе распределительного закона 1-го рода, что приводит к развертыванию исходной конъюнкции ранга 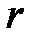в логическую сумму 
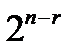КЕ.
Пример. Развернуть конъюнкцию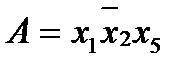 
. Здесь предполагается, что число высказываний 
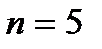, но два из них отсутствуют, тогда:
1. 
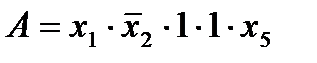
2. 
.
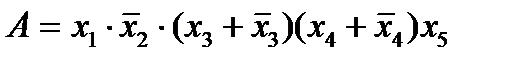3. 
= 
.
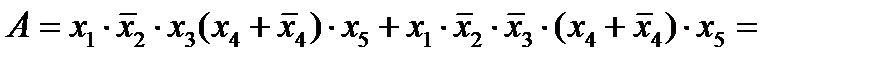
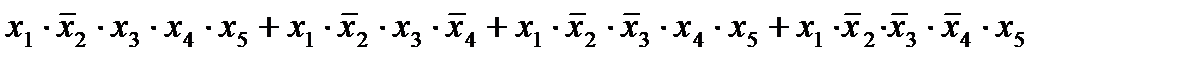2) 2)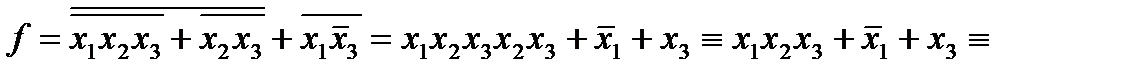 
.
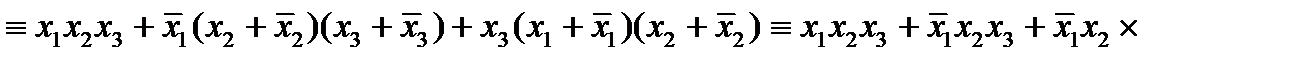
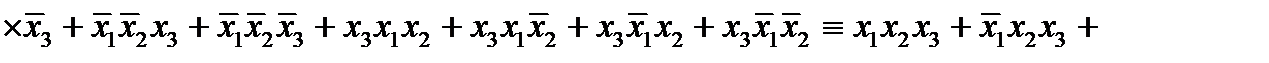
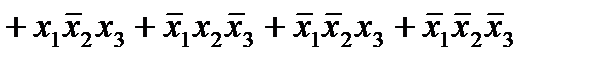Билет 3
1) Сначала введем некоторые понятия. Логическое произведение сумма любого числа высказываний называется элементарным, если сомножители слагаемые в нем являются либо одиночными высказываниями, либо их отрицаниями.
Например: 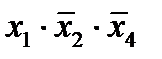– элементарное произведение,
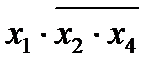– неэлементарное произведение.
Количество сомножителей в элементарном произведении называется его рангом.
Два элементарных произведения одинакового ранга 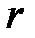называются соседними, если они являются формулами одних и тех же высказываний и отличаются знаком отрицания только одного высказывания.
Теперь сформулируем само правило склеивания для элементарных конъюнкций: логическую сумму двух соседних произведений некоторого ранга 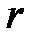можно заменить одним элементарным произведением ранга 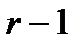, являющимся общей частью исходных слагаемых.
Пример: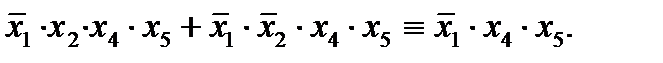
Аналогично для дизъюнкции определяются ранг и соседство. Правило склеивания для элементарных дизъюнкций формулируется следующим образом: логическое произведение двух соседних дизъюнкций ранга 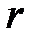можно заменить одной дизъюнкцией ранга 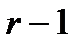, являющейся общей частью исходных сомножителей.
Пример: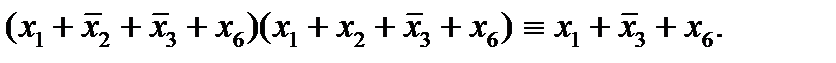
2) ХЗ