Построение проверяющего и диагностическоготестов для комбинационных схем на логических элементах
Логический элемент ЛЭ представляет собой устройство (рисунок 3.1), имеющее n входов и один выход, на котором реализуется некоторая функция алгебры логики (ФАЛ) F(х). Неисправность во внутренней структуре ЛЭ приводит к тому, что на его выходе вместо функции F(х) реализуется функция неисправности f(x). Тест проверки ЛЭ должен определить, какую из функций[F(x) или f(x)]реализует элемент. Число и вид функций неисправности зависят от внутренней структуры ЛЭ. Анализ неисправностей и построение теста ЛЭ выполняют при помощи ТФН.
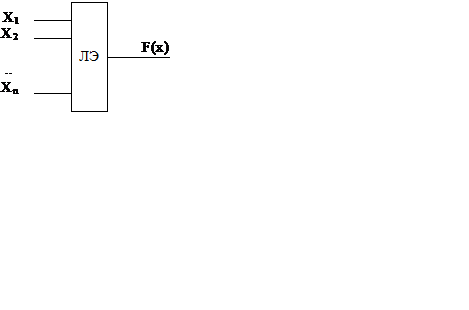
Рисунок 3.1 – Логический элемент
Существуют константные неисправности. Такие неисправности можно инвертировать как фиксацию в константу (нуль или единица) сигнала на входе или выходе ЛЭ. Например, обрыв входа элемента ИЛИ-НЕ соответствует фиксации на нем нулевого сигнала, обрыв перехода Э–К транзистора — фиксации на выходе элемента единичного сигнала и т. д. В общем случае, элемент с n входами может иметь 2n+2 константные неисправности, так как каждые вход и выход могут быть зафиксированы как в нуль, так и в единицу. На схемах константные неисправности обозначают в виде кружков, расположенных около соответствующих входов и выходов (пример приведен на рисунке 3.2). Верхние кружки соответствуют неисправностям “константа 1” (К ® 1), а нижние – неисправностям “константа 0” (К® 0). Как правило, ЛЭ имеет только один вид неисправности на входе.
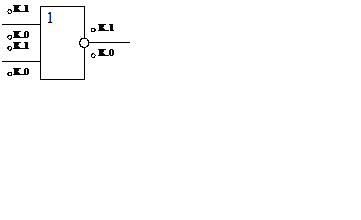
Рисунок 3.2 – Обозначение константных неисправностей
Для ЛЭ можно выделить классы эквивалентных неисправностей, которые показаны на рисунке 3.3 в виде графов, нанесенных на изображение элементов.
Эквивалентные неисправности соединены прямыми линиями. Рассмотрим, например, элемент ИЛИ.
В класс эквивалентных неисправностей входят неисправности 1, 3 и 5, соответствующие неисправностям вида К® 1 входов и выхода элемента. Очевидно, что если на каком-либо входе зафиксировать сигнал единицу, то такой же сигнал фиксируется на выходе.
При этом по выходу элемента невозможно определить, где имеет место неисправность – на каком входе или выходе. Для этих неисправностей равны функции неисправности (f1=f3=f5) и проверяющие функции.
При построении Тп и Тд от класса эквивалентных неисправностей рассматривается только один ее представитель.
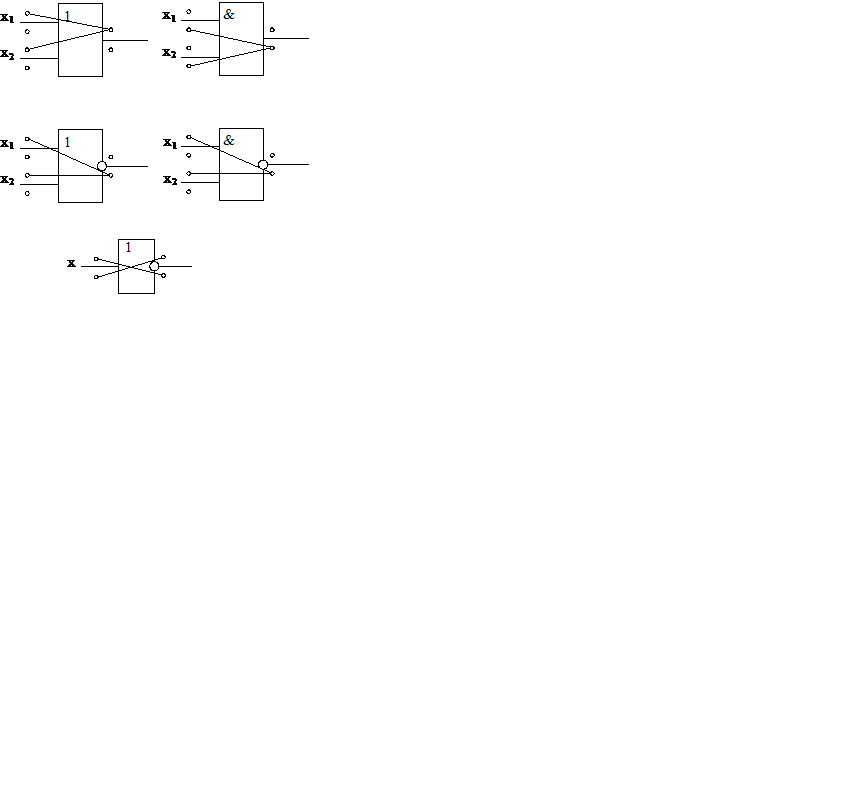
Рисунок 3.3 – Классы эквивалентных неисправностей для логических элементов
Среди константных неисправностей выделяются импликантные неисправности. Неисправность Ni , находится в отношении импликации к неисправности Nj, (обозначается: Ni®Nj), если на тех входных наборах, на которых равна единице проверяющая функция неисправности Niφi , равна также единице и проверяющая функция неисправности Njφj (φi®φj). Отношение импликации указывается на изображениях элементов в виде стрелок, направляющих от Ni к Nj.
Комбинационная схема содержит логические элементы и связи (соединения) между ними. В ней возможны следующие дефекты: неисправности ЛЭ: обрывы соединений, замыкания между соединениями (в том числе с шинами питания), перепутывание связей (неправильный монтаж).
Для диагностирования задана следующая функция:
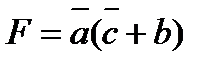
Логическая схема, исполняющая данную функцию будет выглядеть следующим образом:
Рисунок 3.4 Логическая схема функции F
Необходимо нанести неисправности компонент схемы. Под компонентами понимают входы и выходы элементов, и входы схемы.
Если выход элемента или вход схемы соединен с входом только одного элемента, то это соединение рассматривают как одну компоненту. Если в схеме имеется точка разветвления, то в качестве компонент выступают как точки разветвления, так и все ветви разветвления. Для каждой компоненты указывают две константные неисправности К->1 и К->0.
Для каждого логического элемента наносятся графы эквивалентных неисправностей и указывают отношения импликации между неисправностями, в результате чего устанавливают отношения между неисправностями для всей схемы.
Нумеруются неисправности, причем среди эквивалентных неисправностей нумеруют только одну, ближе всех расположенную к выходу (для нее наиболее просто вычислить проверяющую функцию); все неисправности, к которым направлены дуги, не нумеруют; если хотя бы к одной из эквивалентных неисправностей направлена дуга, то ни одну из них не нумеруют. В результате данной операции сокращают список неисправностей, которые необходимо рассматривать при построении теста. В данной схеме пронумеровано 7неисправностей.
Рисунок 3.5 Логическая схема функции F с обозначением неисправностей
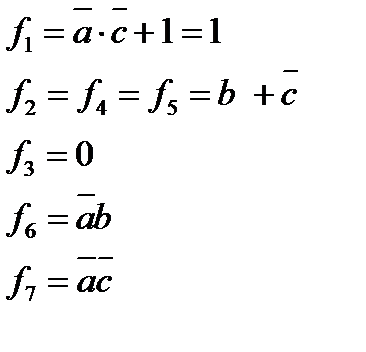
Составляем ТФН
Таблица 3.1 – Таблица ТФН для функции F
| Входнойнабор | F | f1 | f2 | f3 | f4 | f5 | f6 | f7 | |
| № | abc | ||||||||
Составим проверяющие функции по таблице:
φ1 =1v4v5v6v7
φ2= 3
φ3= 1v2v3
φ4= 3
φ5= 3
φ6= 1
φ7= 1
На основании проверяющих функций проверяющий тест будет иметь следующий вид:
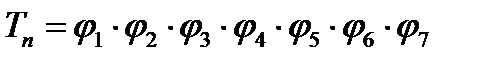 (3.1)
(3.1)
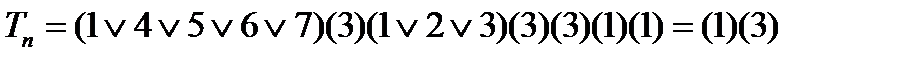
В результате получаем 1минимальный тест:
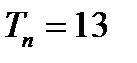
При расчете диагностического теста,не учитывают отношения импликации между неисправностями. На схему наносят только графы эквивалентных неисправностей, которые нумеруют в соответствии с указанным для них правилом. В результате число неисправностей, включаемых в ТФН, увеличивается. В нашем случае в ТФН дополнительно включаются обе неисправности выхода элемента ИЛИ. По диагностическому тесту строят словарь неисправностей.
Рисунок 3.6 Логическая схема функции F для составления диагностического теста
Составим ТФН.
Таблица 3.2 – Таблица ТФН
| Входнойнабор | F | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | |
| № | abc | |||||||||||
Определим различающиефункции:
1)φ1,2=1v3v4v5v6v7
φ1,3=0v1v2v3v4v5v6v7
φ1,4=1v3v4v5v6v7
φ1,5=1v3v4v5v6v7
φ1,6=4v5v6v7
φ1,7=4v5v6v7
φ1,9=0v1v2v3v4v5v6v7
φ1,10=0v1v4v5v6v7
2)φ2,3=0v2
φ2,6=1v3
φ2,7=1v3
φ2,8=1v3v4v5v6v7
φ2,9=0v2
φ2,10=0v2v3
3)φ3,4=0v2
φ3,5=0v2
φ3,6=0v1v2v3
φ3,7=0v1v2v3
φ3,8=0v1v2v3v4v5v6v7
φ3,10=2v3
4)φ4,6=1v3
φ4,7=1v3
φ4,8=1v3v4v5v6v7
φ4,9=0v2
φ4,10= 0v3
5)φ5,6=1v3
φ5,7=1v3
φ5,8=1v3v4v5v6v7
φ5,9=0v2
φ5,10=0v3
6)φ6,8=4v5v6v7
φ6,9= 0v1v2v3
φ6,10=0v1
7)φ7,8=4v5v6v7
φ7,9=0v1v2v3
φ7,10=0v1
8)φ8,9=0v1v2v3v4v5v6v7
φ8,10=0v1v4v5v6v7
9)φ9,10=2v3
Составим диагностический тест, используя формулы алгебры-логики:
Тд = φ1,2 φ1,3 . . . φn-1,n (3.2)
Тд= (1v3v4v5v6v7)(0v1v2v3v4v5v6v7)(1v3v4v5v6v7)(1v3v4v5v6v7)
(4v5v6v7)(4v5v6v7)(0v1v2v3v4v5v6v7)(0v1v4v5v6v7)(0v2)(1v3)(1v3)
(1v3v4v5v6v7)(0v2)(0v2)(0v2)(0v1v2v3)(0v1v2v3)(0v1v2v3v4v5v6v7)
(2v3)(1v3)(1v3)(1v3v4v5v6v7)(0v2)(0v3)(1v3)(1v3)(1v3v4v5v6v7)(0v2)
(0v3)(4v5v6v7)(0v1v2v3)(0v1)(4v5v6v7)(0v1v2v3)(0v1)(0v1v2v3v4v5v6v7)
(0v1v4v5v6v7)(2v3)= (0v2)(0v1v2v3)(1v3)(1v3v4v5v6v7)(2v3)(0v1)
(0v1v4v5v6v7)(0v3) (0v1v2v3v4v5v6v7)= (0v2)(2v3)(1v3)(0v1)(0v3)=
=0(1v2v3)3(1v2)=03(1v2)
Один из минимальных тестов
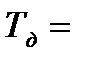 0123
0123
Для упрощения выражения я применил формулы поглощения, и преобразовал выражение к наименьшему числу слагаемых с наименьшим числом множителей.
Аналогичную ситуацию мы проделаем с Тд”
Тд” = Тпφ1,2φ1,3 . . = ТпТд (3.3)
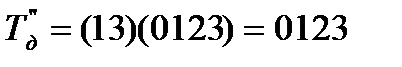
Таблица 3.3 - Словарь неисправностей для Тд
| Входнойнабор | F | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | |
| № | abc | |||||||||||
Таблица 3.4 - Словарь неисправностей для Тд”
| Входнойнабор | F | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | |
| № | abc | |||||||||||
Заключение
На железных дорогах РФ техническая диагностика имеет большое значение. Залогом надежной и бесперебойной работы является постоянный контроль состояния объектов с целью выявления или предупреждения неисправностей. Знание методов построения диагностического и проверяющего тестов для различных систем дает возможность диагностировать работу любого устройства ЖАТС.
Студентам электротехнического факультета как будущим инженерам необходимо разбираться в вопросах диагностики и мониторинга, особенно учитывая то, что уже в ближайшем будущем необходимо создавать системы способные не только измерять параметры объекта, но и предсказывать предотказное состояние.
В общем случае можно сказать, что диагностирование – это одно из ключевых понятий в системах железнодорожной автоматики и телемеханики, дающая в действительности множество полезных в практике результатов и позволяющая находить неисправные элементы подачей каких-либо наборов или слежкой за изменением состояния каких-либо элементов.
В результате выполнения курсовой работы были построены проверяющие и диагностические тесты для непрерывной системы. Выполнено построение теста для комбинационной релейно-контактной схемы и тесты методом цепей и сечений. Построены тесты для комбинационных схем на логических элементах. По полученным тестам были построены таблицы функцийнеисправностей и словари неисправностей.
Список литературы
1. Коваленко В.Н.Построение проверяющих и диагностических тестов. Методическое пособие и задания к курсовой работе по дисциплине «Основы технической диагностики устройств железнодорожной автоматики, телемеханики и связи» - Екатеринбург: УрГУПС, 2005.-43с.
2. Дмитриенко И.Е., Сапожников В.В., Дьяков Д.В. Измерение и диагностирование в системах железнодорожной автоматики, телемеханики и связи, Учебник для вузов ж.-д. транспорт - М: Транспорт, 1994.-263с.
Размещено на Allbest.ru
