Лабораторные работы по технологии программирования

Лабораторные работы по технологии программирования

Требования к лабораторным работам

Содержание отчета:

1. Титульный лист взять на сайте кафедры ИСУ

2. Текст задания

3. Текст программы с комментариями

4. Описание функций (Пункты меню). Входные и выходные значение и для чего используется каждая функция.

5. Принтскрины экранов с входными и выходными данные.

6. Используемая литература.

В процессе учебы и сдачи могут быть вынесены дополнительные требования.

Лабораторная работа № 1 Списки. Стеки. Очереди.

Задача 1.Вводится последовательность, состоящая из N пар символов (a_i,b_i). Каждая пара определяет порядок предшествования символов, например, пара (b,с) означает, что символ "b" предшествует символу "с". Из порядка (b,с) и (с,a) следует порядок (b,a). Необходимо определить, является ли введенная последовательность:

а) полной, т.е. все использованные для формирования пар символы (выбросив повторяющиеся) можно выстроить в цепочку (A1,A2,...,As) в порядке предшествования;

б) противоречивой, т.е. для некоторых символов x,y можно получить одновременно порядок как (x,y) так и (y,x);

--------------------------------------------------------------------------------

Задача 2. Вокруг считающего стоит N человек, из которых выделен первый, а остальные занумерованы по часовой стрелке числами от 2 до N. Считающий, начиная с кого-то, ведет счет до M. Человек на котором остановился счет, выходит из круга. Счет продолжается со следующего человека и так до тех пор, пока не останется один человек.

Определить

a) номер оставшегося человека, если известно M и то, что счет начинался с первого человека;

b) номер человека c которого начинался счет, если известно M и номер оставшегося человека L.

--------------------------------------------------------------------------------

Задача 3. Задана полоска длиной 2^k клеток и шириной в одну клетку. Полоску сгибают пополам так, чтобы правая половинка оказалась под левой. Сгибание продолжают до тех пор, пока сверху находится больше одной клетки. Необходимо пронумеровать клетки таким образом, чтобы после окончания сгибания полосы номера клеток в получившейся колонке были расположены в порядке 1,2,3,4,...,2^k.

--------------------------------------------------------------------------------

Задача 4. Квадрат разбит на 4^k равновеликих квадратных клеток. Квадрат перегибается поочередно относительно вертикальной (правая половина подкладывается под левую) и горизонтальной (нижняя половина подкладывается под верхнюю) оси симметрии до тех пор, пока все клетки не будут расположены друг под другом. Требуется занумеровать клетки исходного квадрата таким образом, чтобы в результате выполнения операций перегиба номера клеток, расположенных друг под другом, образовали числовую последовательность 1,2,3,...,4^k, начиная с верхней клетки.

--------------------------------------------------------------------------------

Задача 5. Дана конечная последовательность, состоящая из левых и правых скобок pазличных заданных типов( «(» «{» «[»«)» «}» «]»). Определить, можно ли добавить в нее цифры и знаки арифметических действий так, чтобы получилось правильное арифметическое выражение.

--------------------------------------------------------------------------------

Задача 6. В таблице А размера N за один просмотр необходимо каждый элемент заменить на ближайший следующий за ним элемент, который больше его. Если такого элемента нет, то заменить его на ноль.

ПРИМЕР А=1 3 2 5 3 4

ОТВЕТ А=3 5 5 0 4 0

--------------------------------------------------------------------------------

Задача 7. Одинокий король долго ходил по бесконечной шахматной доске. Известна последовательность из N его ходов (вверх, вниз, влево, вправо, вверх-влево и т.п.).Написать программу, определяющую побывал ли король дважды на одном и том же поле за минимально возможное при заданном N число вычислений.

--------------------------------------------------------------------------------

Задача 8 По кругу расположено N монет гербами вверх и M монет гербами вниз. Обходя круг по ходу часовой стрелки, переворачивает каждую S -тую монету. В первый раз счет начинается с герба. В каком порядке надо расставить монеты, чтобы после K ходов стало L монет, лежащих гербами вверх.

--------------------------------------------------------------------------------

Задача 9.

N серых и M белых мышей сидят по кругу. Кошка ходит по кругу по часовой стрелке и съедает каждую S -тую мышку. В первый раз счет начинается с серой мышки. Составить алгоритм определяющий порядок в котором сидели мышки, если через некоторое время осталось K серых и L белых мышей.

--------------------------------------------------------------------------------

Задача 10.

Из листа клетчатой бумаги размером М*N клеток удалили некоторые клетки. На сколько кусков распадется оставшаяся часть листа?

Пример. Если из шахматной доски удалить все клетки одного цвета, то оставшаяся часть распадется на 32 куска.

--------------------------------------------------------------------------------

Задача 11.

Имеется n черных и белых карточек, сложенных в стопку. Карточки раскладываются на стол в одну линию следующим образом: первая кладется на стол, вторая под низ стопки, третья- на стол, четвертая - под низ стопки и т.д., пока все карточки не будут выложены на стол. Каким должно быть исходное расположение карточек в стопке, чтобы разложенные на столе карточки чередовались по цвету: белая, черная, белая, черная и т.д.

--------------------------------------------------------------------------------

Задача 12.

Есть министерство из N чиновников, где N натуральное число. У каждого из чиновников могут быть как подчиненные, так и начальники, причем справедливы правила: подчиненные моего подчиненного мои подчиненные, начальники моего начальника - мои начальники, мой начальник не есть мой подчиненный, у каждого чиновника не более одного непосредственного начальника.

Для того чтобы получить лицензию на вывоз меди необходимо получить подпись 1-ого чиновника - начальника всех чиновников. Проблема осложняется тем, что каждый чиновник, вообще говоря, может потребовать "визы", т.е. подписи некоторых своих непосредственных подчиненных и взятку - известное количество долларов. Для каждого чиновника известен непустой список возможных наборов "виз" и соответствующая каждому набору взятка. Пустой набор означает, что данный чиновник не требует виз в данном случае. Чиновник ставит свою подпись лишь после того, как ему представлены все подписи одного из наборов "виз" и уплачена соответствующая взятка.

Необходимо определить и вывести минимальный по сумме уплаченных взяток допустимый порядок получения подписей для лицензии и стоимость.

N<100. Количество наборов для каждого чиновника не превосходит 15.

--------------------------------------------------------------------------------

Задача 13.. Объединить n списков в один список

-----------------------------------------------------------------------------------------------------------------

Задача 14. Поменять местами два элемента в списке

-----------------------------------------------------------------------------------------------------------------

Задача 15. Добавить новый элемент в список перед заданным элементом

-----------------------------------------------------------------------------------------------------------------

Задача 16. Удалить из списка неупорядоченные подсписки

-----------------------------------------------------------------------------------------------------------------

Задача 17. Сделать определённый элемент в списке первым

-----------------------------------------------------------------------------------------------------------------

Задача 18. Реализовать удаление элементов из очереди с приоритетом. Очередь с приоритетом – первым включается – с высшим приоритетом исключается

-----------------------------------------------------------------------------------------------------------------

Задача 19. Реализовать функции работы со стеком (удаление, вставка).

--------------------------------------------------------------------------------

Задача 20.

1. Дана величина a строкового типа из четного количества символов. Получить и напечатать величину b, состоящую из символов первой половины величины a, записанных в обратном порядке, после которых идут символы второй половины величины a, также записанные в обратном порядке. Например, при а = “привет” b должно быть равно “ипртев”.

--------------------------------------------------------------------------------

Задача 21.

Написать процедуру, которая меняла бы в односвязном списке крайние элементы.

--------------------------------------------------------------------------------

Задача22.

Даны четыре стека. Два первых стека пустые, а в двух других находятся натуральные числа. В первый пустой стек поместить четные числа в порядке не убывания, взятые из непустых стеков, во второй пустой стек поместить нечетные числа в порядке не возрастания, так же взятые их непустых стеков. Предполагается, что множества четных чисел и нечетных чисел непустые.

--------------------------------------------------------------------------------

Задача 23.

Используя список, удалить из текста программы комментарии и поместить их в отдельных текстовый файл.

--------------------------------------------------------------------------------

Задача 24.

Дан список вещественных чисел. Все его элементы, не равные нулю, переписать, сохраняя порядок, в начало списка, а нулевые элементы в конец списка. Новый список заводить нельзя.

--------------------------------------------------------------------------------

Задача 25.

Используя очередь, отредактировать текст, оставляя один пробел в каждой серии пробелов.

--------------------------------------------------------------------------------

Задача 26.

Используя список, удалить их текста заданный набор букв.

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

Задача**.

Система состоит из двух процессоров P1 и P2, двух стеков S1 и S2 и четырёх очередей F1, F2, F3, F4. В систему могут поступать запросы на выполнение задач двух приоритетов - высший (1) и низший (2). Задачи сначала обрабатываются последовательно процессором P1, затем P2.

Запросы на выполнение задач высшего приоритета, поступающие из генератора задач, ставятся в очередь F1, а поступающие с процессора P1 - в очередь F3. Запросы на выполнение задач низшего приоритета, поступающие с генератора задач, ставятся в очередь F2, а поступающие с процессора P1 - в очередь F4. Процессор P1 обрабатывает запросы из очередей F1 и F2, а процессор P2 - из очередей F3 и F4. Процессор сначала обрабатывает задачи из очереди задач с высшим приоритетом, затем из очереди задач с низшим приоритетом. Если процессор выполняет задачу с низшим приоритетом и приходит запрос на выполнение задачи с высшим приоритетом, то выполняемая задача помещается в соответствующий процессору стек, а пришедшая задача - в процессор. Задача из стека возвращается в процессор, если все задачи большего приоритета обработаны.

--------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------

1.4.

Какуро

Хитори

Китайская стена

Филиппинский кроссворд

Японская мозаика

Морской бой

Мосты

Ожерелье

Фонари

Филломино

Неравенство

Куромасу

Нурикабе

Лагерь

Кен-кен

Хидато

Нумератор

Квадраты

Галактики

Небоскрёбы

Волновой эффект

Гранд тур

Первые встречные

Облако

Бумеранг

Сапёр

27. Сапёр + Морской бой

Комнаты

Числобус

Сто

Стрелки

Матракс

Стрейтс

Линейщик

Двоичный код

Стены

Домино-пасьянс

Лоскутки

Особняки

Рекуто

Соседи

Роза ветров

Шака-шака

Какурасу

Мочикоро

Двери

Маяки

Тапа

Четвёртый лишний

Какуро ("Kakuro") - это числовая головоломка, математический эквивалент кроссворда. Необходимо вставить в клетки цифры от 1 до 9, причем некоторые клетки неактивны (такие клетки помечены черным цветом). В клетках с заданными числовыми значениями правое верхнее значение означает сумму цифр в ряду, а значение снизу слева равно сумме цифр столбца ниже клетки. Например, число 6 можно представить как сумму 1 и 5, 2 и 4; одинаковые цифры (3 и 3) использовать запрещено.

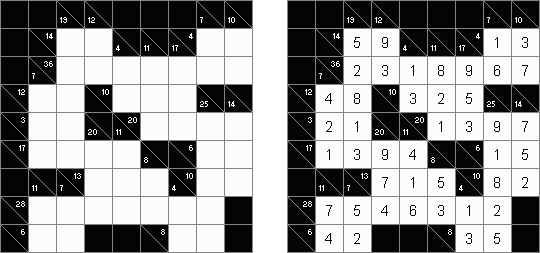
Хитори ("Hitori") - это логическая головоломка. Необходимо вычеркивать повторяющиеся числа, чтобы ни одна из них не встречалась в любой строке или столбце чаще одного раза. Зачеркнутые клетки могут касаться друг друга только углами, но никак не сторонами. Незачеркнутые клетки должны составлять непрерывное "белое" пространство, то есть ни одна из них не должна быть изолирована от других таких же.

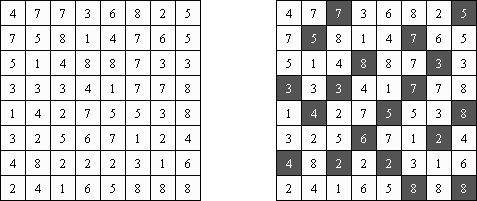
Китайская стена ("Slitherlink", "Fences", "Loop the Loop", "Dotty Dilemma", "Sli-Lin"; еще одно название - Скользящие линии) - это логическая головоломка, напоминающая лабиринт. Необходимо соединить точки вертикальными и горизонтальными прямыми отрезками так, чтобы получилась единая замкнутая цепь, не пересекающая саму себя. Каждая цифра указывает, сколько отрезков должно расположиться вокруг нее по периметру. Если в ячейке нет цифры, то вокруг нее может быть любое количество линий.

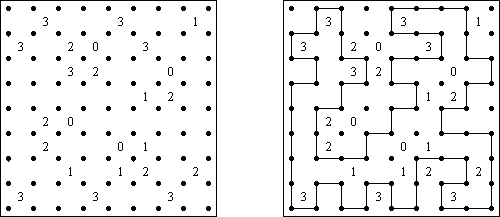
Филиппинский кроссворд ("Link-a-Pix", "Paint by Pairs") - это головоломка с числами. Все числа, расположенные в сетке, кроме единицы, имеют свою пару. Необходимо найти каждую пару чисел и соединить их линиями. Количество клеток в ней должно равняться числам на ее концах. Линии, соединяющие пары, могут преломляться и идти в горизонтальном или вертикальном направлениях (но не по диагоналям). Линии не могут пересекаться друг с другом или проходить через одни и те же клетки.

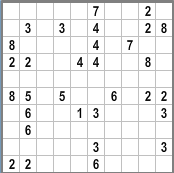
Японская мозаика ("Fill-a-Pix", "Mosaik", "Nurie Puzzle", "Nampre Puzzle") - это логическая головоломка, в которой с помощью цифр зашифрована картинка. Каждое из чисел означает, сколько примыкающих клеток (считая ту, что с цифрой) должно быть закрашено. Например, если в клетке стоит ноль, то ни эта клетка, ни соседствующие с ней закрашены не будут.

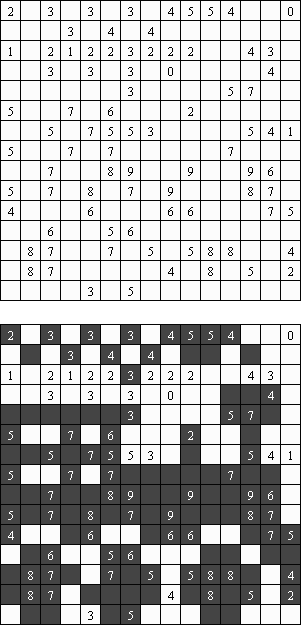
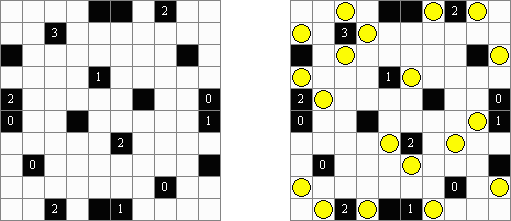
Морской бой ("Battleships", "Solitaire Battleships", "Battleship Solitaire") - это головоломка, правила которой похожи на известную игру. Необходимо расположить "корабли" так, чтобы они не соприкасались даже углами. Цифры сбоку и снизу означают, сколько всего фрагментов кораблей попало в эту строку или столбец.

Стандартные размеры поля - 10 x 10. Имеются один корабль, занимающий 4 клетки, два корабля, занимающие 3 клетки, три корабля из 2 клеток и четыре корабль размером в 1 клетку. Иногда некоторые из фрагментов кораблей уже открыты.

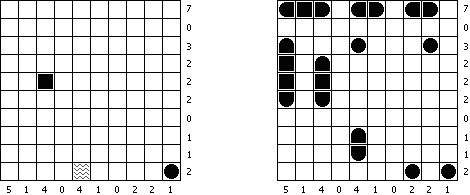
Мосты ("Hashiwokakero", "Hashi", "Bridges", "Chopsticks", "Ai-Ki-Ai") - головоломка, в которой необходимо соединить кружки с цифрами ("острова") прямыми линиями ("мостами"). Цифра на острове показывает, сколько мостов должно быть к нему проложено. Изолированных островов быть не должно; линии должны быть проведены таким образом, чтобы с любого острова по построенным мостам можно было попасть на любой остров.

Между двумя островами разрешается строить не больше двух мостов. Линии могут проходить по горизонтали и вертикали, но не по диагонали. Они не должны преломляться, пересекаться или проходить сквозь острова.

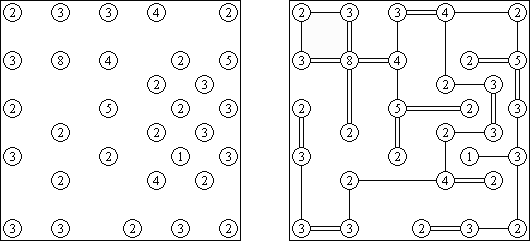
Ожерелье ("Masyu", "Shiroshinju Kuroshinju", "White pearls and black pearls") - это логическая головоломка, в которой необходимо соединить белые и черные круги вертикальными и горизонтальными прямыми отрезками так, чтобы получилась единая замкнутая линия, не пересекающая саму себя. Через белые круги линия проходит прямо, но должна повернуть в предыдущей или следующей клетке (или в обеих этих клетках). Когда линия пересекает черный круг, она должна повернуть на 90 градусов, при этом в предыдущей и следующей клетке повороты запрещены.

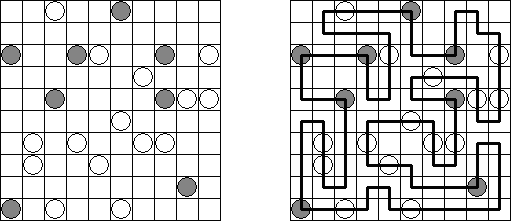
Фонари ("Light Up", "Akari", "Bijutsukan") - это логическая головоломка. Игровое поле состоит из белых и черных клеток; в некоторых черных клетках расположены числа. Необходимо разместить "светильники" в белых клетках таким образом, чтобы все игровое поле было освещено, но фонари не "светили" бы друг на друга.

Свет фонаря распространяется по горизонтали и по вертикали, но может быть заблокирован черной клеткой. В черной клетке может находиться число от 0 до 4, указывая, сколько фонарей должно быть размещено рядом с ней (не учитываются фонари, помещенные по диагонали от этой черной клетки). Если клетка не содержит числа, около нее может быть размещено любое количество фонарей.

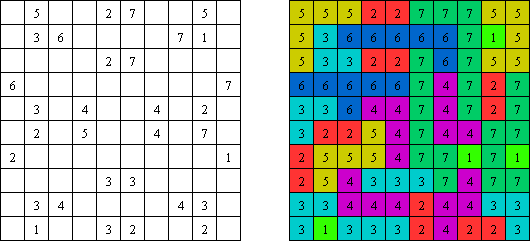
Филломино ("Fillomino") представляет собой прямоугольную сетку произвольного размера; в некоторых клетках находятся числа. Необходимо разбить игровое поле на блоки; блок должен содержать столько клеток, сколько обозначено числом в клетках блока. Блоки, имеющие одинаковый размер, не должны соприкасаться по горизонтали или по вертикали. Клетки, которые изначально не содержали чисел, также могут быть объединены в блоки, необходимые для решения головоломки.

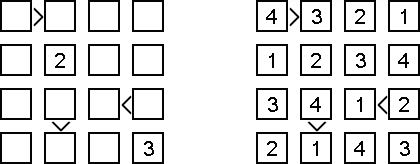
Неравенство ("Futoshiki", "Hutoshiki", "Unequal") - это логическая головоломка с числами. Игровое поле представляет собой квадратную сетку; в некоторых клетках могут стоять цифры; между клетками могут присутствовать знаки "<" и ">", которые показывают соотношения, установленные между соседними цифрами. Необходимо заполнить свободные клетки цифрами так, чтобы в каждой строке и в каждом столбце каждая цифра встречалась бы только один раз.

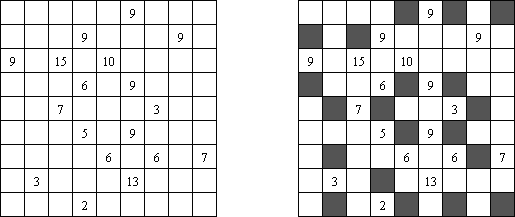
Куромасу ("Kuromasu", "Kurodoko", "Where is black cells?") представляет собой прямоугольную сетку, в некоторых клетках которой могут стоять числа. Необходимо закрасить черным цветом клетки, соблюдая следующие условия:

• каждое число означает, сколько белых клеток "видно" из данной клетки по вертикали и по горизонтали; "взгляд" простирается до тех пор, пока не достигнет края поля или на пути не встретится клетка черного цвета;
• клетки с числами всегда остаются белыми;
• черные клетки не могут соприкасаться по вертикали или по горизонтали;
• все белые клетки составляют единое белое поле, то есть соприкасаются по вертикали или по горизонтали.

Нурикабе ("Nurikabe", "Cell Structure", "Islands in the Stream") - логическая головоломка с числами. В японской мифологии "нурикабе" - это чудовище в виде большой невидимой стены, загораживающей проход.

Необходимо восстановить карту, на которой изображено расположение островов, соблюдая следующие правила:

• информация о каждом острове представлена в виде числа, показывающего количество клеток, которые занимает этот остров;
• любые два острова могут соприкасаться только углами;
• все острова содержат в своем описании только одно число;
• между островами протекает река;
• все клетки реки должны быть соединены между собой;
• на карте не должно присутствовать ни одного квадрата размерами 2 x 2, все клетки которого содержат реку.

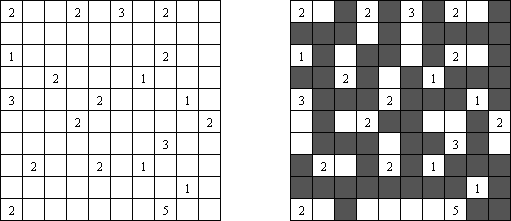
Лагерь ("Tents", "Tents and Trees") представляет собой прямоугольную сетку, некоторые клетки которой содержат "деревья". Необходимо разместить рядом с деревьями "палатки", соблюдая следующие правила:

• Число палаток равняется числу деревьев.
• Каждая палатка располагается рядом со "своим" деревом по горизонтали или вертикали, но не по диагонали. Если это условие выполнено, расположение по отношению к "чужим" деревьям значения не имеет.
• Две палатки не могут располагаться в соседних клетках, в том числе и по диагонали.
• Числа сбоку и сверху означают, сколько палаток находится в этой строке или столбце.

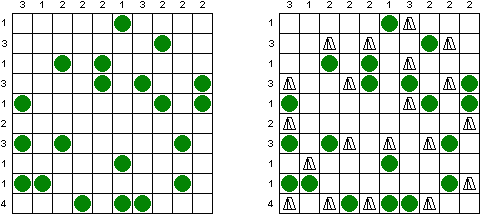
Кен-кен ("KenKen", "KENKEN", "KenDoku", "CalcuDoku", "Square Wisdom") - это математическая и логическая головоломка. Необходимо заполнить сетку цифрами так, чтобы в каждой строке и в каждом столбце они не повторялись. Число в углу каждого выделенного блока является результатом арифметической операции над цифрами в этом блоке. В отличие от судоку-убийцы (сум-до-ку), цифры внутри блока могут повторяться.

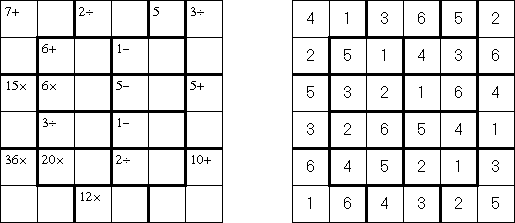
Хидато ("Hidato"; в переводе с идиш: "моя головоломка"; еще одно название - "Hidoku") была изобретена израильским математиком Гиором Бенедеком (Gyora Benedek). Головоломка представляет собой поле произвольной формы (чаще всего прямоугольное или квадратное), состоящее из клеток. Необходимо заполнить все клетки последовательными числами, которые соединены горизонтально, вертикально или по диагонали. В каждой головоломке уже присутствуют наименьшее и наибольшее числа. Также на поле могут стоять и другие числа, чтобы облегчить игроку процесс разгадывания и обеспечить единственность решения задачи.

В России головоломку еще называют "Путь короля", так как движение от одного числа к другому напоминает перемещение шахматного короля по доске.

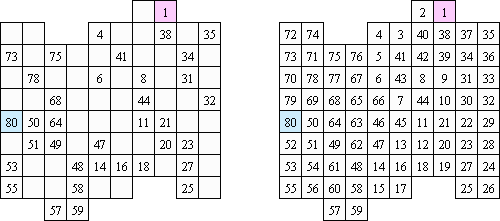
Нумератор ("Numbrix") - вид логической головоломки. Представляет собой прямоугольную сетку, в некоторых клетках которой стоят числа. Требуется заполнить пустые клетки таким образом, чтобы все числа были соединены последовательно, по горизонтали или вертикали. Перемещение по диагонали не допускается.

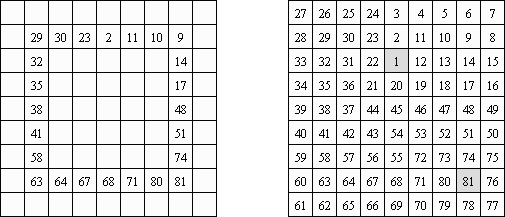
Квадраты ("Shikaku", "Divide by Squares", "Divide by Box", "Number Area") - это логическая головоломка. Она представляет собой прямоугольную сетку без стандартного размера. Некоторые клетки сетки содержат числа. Необходимо прочертить линии, разделяющие сетку на прямоугольные и квадратные регионы таким образом, чтобы каждый регион содержал только одно число, равное площади этого региона.

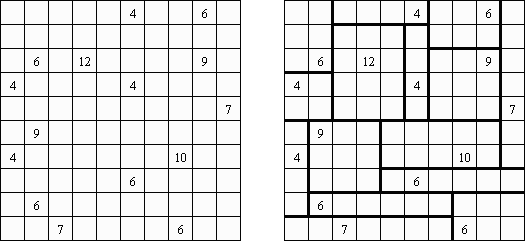
Галактики ("Galaxies", "Tentai Show") - это задача, соединяющая в себе логику и геометрию. Головоломка представляет собой прямоугольную сетку с точками. Необходимо разделить сетку на регионы; каждый регион должен содержать только одну точку. Точка является центром симметрии региона.

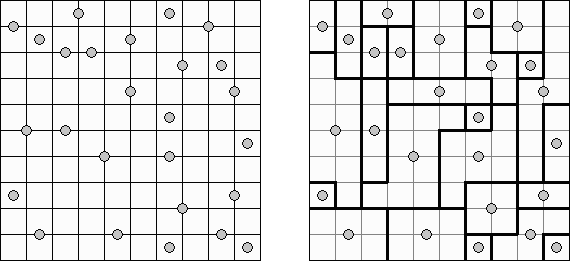
Небоскрёбы ("Skyscrapers") - вид логической головоломки. В ней требуется заполнить числами квадрат так, чтобы в каждой строке и в каждом столбце каждое число использовалось лишь единожды. Заполнение нужно делать с помощью ключевых чисел, считая, что в каждой клетке внутри квадрата стоит дом с количеством этажей, равном стоящему в клетке числу, а числа вне поля означают, сколько домов видно в соответствующей строке или столбце, если смотреть от этого числа.

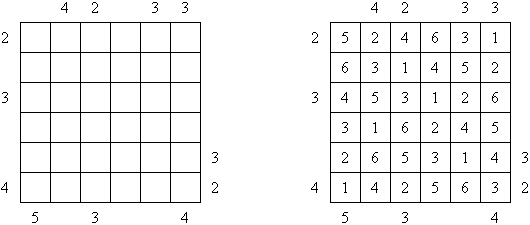
Волновой эффект ("Ripple Effect", "Hakyuu", "Seismic") - вид логической головоломки. Задание состоит из прямоугольной сетки, разделенной на блоки ("комнаты"); в некоторых клетках могут стоять числа. Необходимо заполнить все клетки числами так, чтобы каждый блок содержал числа от 1 до количества клеток в блоке. Если ряд клеток или столбец содержат два одинаковых числа, количество клеток между ними больше или равно этим числам. Например, если столбец содержит две клетки с числом 5, между ними должно быть по крайней мере пять клеток с другими числами.

Гранд тур ("Grand Tour"; еще одно название - Петля с фрагментами) - логическая головоломка, в которой требуется провести не касающуюся и не пересекающую себя замкнутую линию через все точки прямоугольной или квадратной сетки. Для того, чтобы обеспечить единственность решения головоломки, несколько точек уже соединены отрезками.

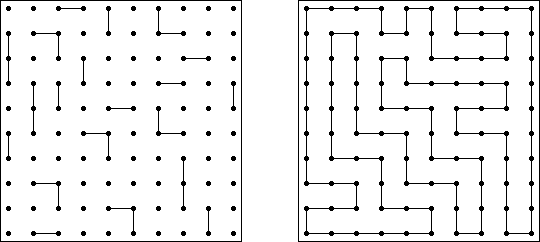
Первые встречные ("Easy as ABC", "ABC End View", "Last Man Standing"; еще одно название - Букварики) - логическая головоломка с буквами. Необходимо заполнить квадратную сетку латинскими буквами (например, от A до E), так чтобы каждый символ встречался в каждой строке и в каждом столбце ровно один раз. Некоторые клетки сетки могут быть пустыми. Буква, стоящая на границе сетки, показывает - какая буква встретится первой в данной строке (столбце).

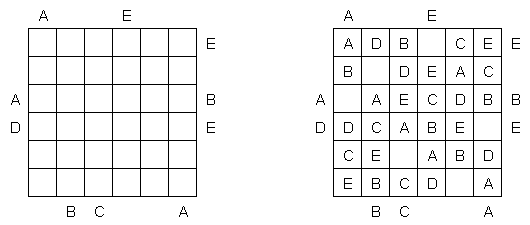
Облака ("Clouds", "Radar"; еще одно название - Синоптик) - это разновидность головоломки "Морской бой". В сетке произвольной формы необходимо расставить прямоугольники ("облака") так, чтобы они не касались друг друга даже углами. Числа по краям сетки означают количество клеток, занятых облаками. Количество и размер облаков не заданы; известно лишь, что стороны прямоугольников имеют длину не меньше двух.

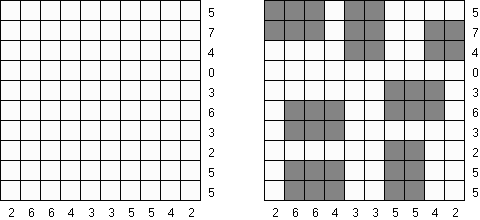
Бумеранг ("Yajilin", "Arrow Ring", "Straight and Arrow") - логическая головоломка квадратной или прямоугольной формы. Задание содержит клетки со стрелками и числами; эта информация необходима для расстановки клеток черного цвета на поле. Цель - нарисовать замкнутую, не пересекающую себя петлю, которая не должна проходить через клетки со стрелками или черные клетки.

• Числа в клетках указывают, сколько именно черных клеток находится в том ряду или том столбце и в том направлении, в котором указывает стрелка. Сами клетки со стрелками не считаются за черные клетки.
• Если клетка не содержит стрелку и не является черной, то она должна содержать сегмент петли.
• Числа в клетках указывают точное число черных клеток. То есть, если ячейка сетки содержит число "3" и стрелку, указывающую влево, это означает, что в ряду слева от такой ячейки располагаются три черных клетки.
• Черные клетки не должны соприкасаться по горизонтали или по вертикали.
• На поле могут быть черные клетки, на которые не указывает ни одна стрелка.

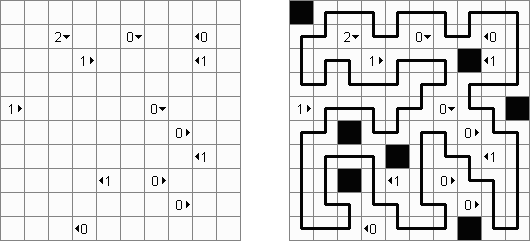
Сапёр ("Minesweeper") известен всем пользователям операционной системы Microsoft Windows. Необходимо расставить "мины" в свободных клетках, используя ключевые числа. Каждое ключевое число показывает, сколько соседних с ним клеток занято минами. Мины расположены по одной в каждой клетке, а в клетке с числом мин не бывает.

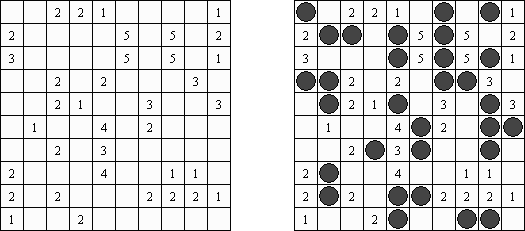
Сапёр + Морской бой ("Minesweeper Battleships") объединяет в себе черты двух популярных головоломок. Необходимо расставить на поле корабли таким образом, чтобы они не касались даже углами. В некоторых клетках сетки стоят цифры. Эти цифры показывают, сколько фрагментов кораблей находится вокруг данной клетки (включая диагонали).

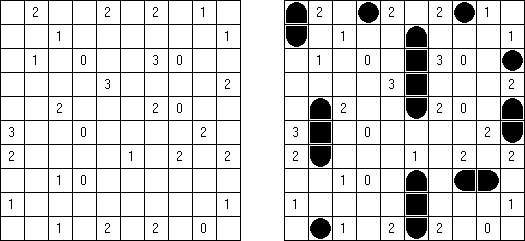
Комнаты ("Heyawake") - логическая головоломка. Она представляет собой прямоугольную сетку, разделенную на блоки ("комнаты"). Некоторые блоки могут содержать числа; число показывает, сколько именно черных клеток должен содержать блок. Если число в блоке отсутствует, такой блок может содержать любое количество черных клеток.

• Черные клетки не должны соприкасаться по горизонтали или по вертикали (только по диагонали).
• Все белые клетки соединены друг с другом по горизонтали или по вертикали.
• Непрерывная линия из белых клеток не должна пересекать более двух "комнат".

Числобус ("Tenner Grid", "From 1 to 10", "Zehnergitter") представляет собой прямоугольную сетку шириной десять клеток. Необходимо заполнить сетку таким образом, чтобы каждый ряд содержал цифры от 0 до 9. В столбцах числа могут повторяться. Число внизу сетки означает сумму всех цифр в столбце. Числа, находящиеся в смежных клетках (даже если клетки соприкасаются лишь по диагонали), должны быть разными.

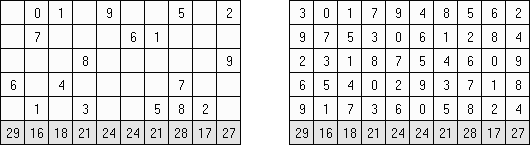
Сто ("Hundred") состоит из квадратной сетки, в каждой клетке которой проставлены цифры. Требуется поставить дополнительные цифры таким образом, чтобы сумма чисел в каждом ряду и каждом столбце была равна 100.

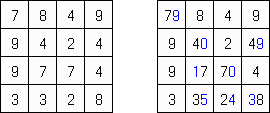
Стрелки ("Arrows") - это разновидность логической головоломки. Она состоит из сетки прямоугольной или квадратной формы, заполненной числами. Цель головоломки - расставить стрелки за пределами сетки. Каждая стрелка указывает хотя бы на одну клетку с числом. Число означает количество стрелок, указывающих на данную клетку.

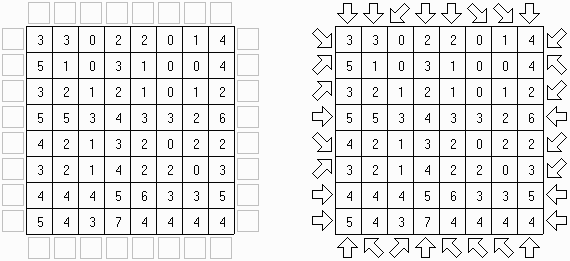
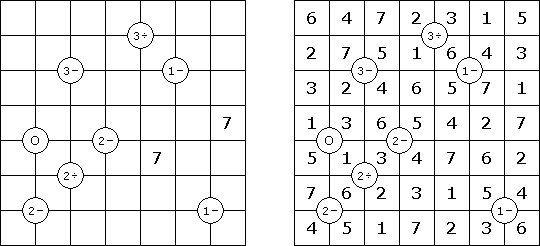
Матракс ("Mathrax") - разновидность логической головоломки. Необходимо заполнить числами квадрат так, чтобы в каждой строке и в каждом столбце каждое число использовалось лишь единожды. Некоторые из чисел уже могут присутствовать в сетке. На пересечениях линий сетки могут располагаться кружки с дополнительными условиями:

• Число и знак арифметического действия (сложение, вычитание, умножение, деление) - число в кружке означает результат выполнения арифметического действия над парами чисел в клетках, примыкающих к кружку и соприкасающихся друг с другом по диагонали.
• Латинская буква "E" - в клетках, примыкающих к кружку, все четыре числа являются чётными ("E" - от английского слова "even", чётный).
• Латинская буква "O" - в клетках вокруг кружка все четыре числа являются нечётными ("O" - от английского слова "odd", нечётный).

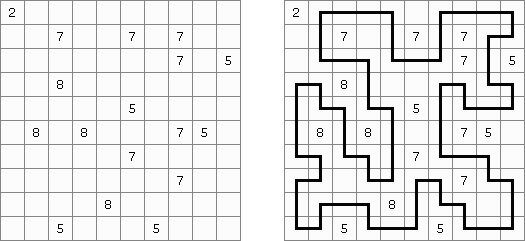
Стрейтс ("Str8ts", "Straights"; от термина в карточной игре покер, обозначающего пять карт по порядку) - логическая головоломка, придуманная Джеффом Виддеричем (Jeff Widderich) из Канады. Сетка квадратной формы содержит черные и белые клетки. Необходимо расставить числа в белых клетках таким образом, чтобы в промежутках между черными клетками образовывались наборы последовательных чисел, но не обязательно в порядке возрастания или убывания (например: 2-1-3-4). В каждой строке и в каждом столбце числа, стоящие в белых и черных клетках, не должны повторяться. Числа в черных клетках не входят в наборы последовательных чисел.

Линейщик ("Linesweeper") - логическая головоломка, правила которой похожи на правила головоломки "Сапёр". Задание представляет собой квадратную или прямоугольную сетку; в некоторых клетках сетки стоят числа (возможны значения от 0 до 8). Необходимо провести замкнутую линию через клетки; линия не должна пересекать саму себя или проходить через клетки с числами. Цифра в клетке показывает, через какое количество клеток, расположенных вокруг клетки с числом, проходит линия.

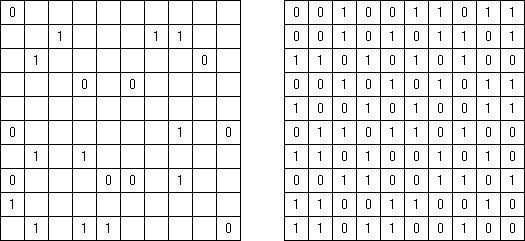
Двоичный код ("Binairo", "Binary Puzzle", "Takuzu", "Tohu wa Vohu") - логическая головоломка с использованием цифр "0" и "1". Прямоугольную или квадратную сетку необходимо заполнить цифрами в соответствии со следующими правилами:

• Каждая строка и каждый столбец содержат столько же цифр "1", как и цифр "0" (или на одну больше для сеток с нечётными размерами).
• Одна и та же цифра может стоять лишь в двух ячейках подряд.
• Каждая строка должна быть уникальной, и каждый столбец должен быть уникальным.

Стены ("Walls") - логическая головоломка; её изобрёл Наоки Инаба (Naoki Inaba) из Японии. Необходимо расставить в белых клетках горизонтальные и вертикальные линии так, чтобы суммарная длина всех "лучей", исходящих из клетки чёрного цвета, совпадала с числом, стоящим в этой клетке.

Домино-пасьянс ("Dominosa", "Dominosa Omnibus", "Solitaire Dominoes", "Domino Hunt") - логическая головоломка, в которой используются костяшки домино. На поле показаны только числа; необходимо восстановить границы между костяшками домино.

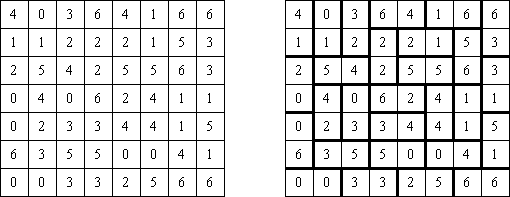
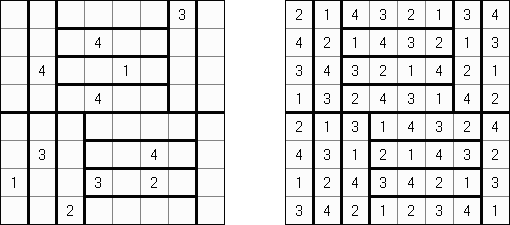
Лоскутки ("Patchwork", "Tatami"; еще одно название - Магические полоски) - головоломка, которая представляет собой квадратную сетку, поделенную на регионы одинакового размера ("комнаты"). Необходимо заполнить каждую комнату цифрами от 1 до числа, равного количеству клеток в регионе. Каждый ряд и каждая колонка должны содержать одинаковые количества каждого вида цифр. Соседние клетки, соприкасающиеся по горизонтали или вертикали, не должны содержать одинаковые цифры.

В некоторых заданиях этой разновидности головоломок используются буквы вместо цифр. Cross+A может решать головоломки как с цифрами, так и с буквами в задании.

Особняки ("Knossos", "Кносс" - древний город и дворец на острове Крит, а также местонахождение лабиринта, в котором был заточён Минотавр) представляет собой прямоугольную или квадратную сетку, в некоторых ячейках которой стоят числа. Необходимо разделить сетку на регионы ("к