Описание нормальных алгоритмов Маркова (НАМ).

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образовании

“Ижевский государственный технический университет имени М.Т.Калашникова” (ИжГТУ)

С.Н.Селивановский,

В.П. Тарануха ,

О.Я. Шамсиахметов

МЕТОДИЧЕСКое руководство

к лабораторной работе по курсу ” Информатика”

направления 211000 “Конструирование и технология электронных средств” профиля ”Проектирование и технология радиоэлектронных средств”

Лабораторная работа № 1

Создание имитационных моделей абстрактных автоматов Тьюринга и Маркова средствами Excel MS Office.

Ижевск 2014

СоставителИ: С.Н.селивановский,доцент

в.п.Тарануха, канд.техн.наук, доцент

шАМСИАХМЕТОВ о.я.

Рецензенты - канд. физ.-мат. наук, доцент Клишин С.В.,

доктор техн. наук, профессор ушаков П.А.

МЕТОДИЧЕСКОЕ РУКОВОДСТВО к лабораторной работе №1 “ Создание имитационных моделей абстрактных автоматов Тьюринга и Маркова средствами Excel MS Office.

. ” пО курсу ” ИНФОРМАТИКА” профиля ”Проектирование и технология радиоэлектронных средств”/ сЕЛИВАНОВСКИЙ с.н.,Тарануха В.П.,ШАМСИАХМЕТОВ О.Я.-: Ижевск: Издательство ИжГТУ, 2014.- 46 с.

Настоящие методические указания определяют последователь­ность выполнения лабораторной работы по дисциплине «ИНФОРМАТИКА» и включают в себя рекомендации ПО СОЗДАНИЮ ПРИКЛАДНЫХ ПРОГРАММ имитационных моделей абстрактных автоматов, А ТАКЖЕ МЕТОДЫ адаптации программного обеспечения к конкретным задачам оптимизации алгоритмов.

© СЕЛИВАНОВСКИЙ С.Н.,Тарануха В.П.,шамсиахметов О.Я.

© ИжГТУ, 2014

Краткая теория.

Описание машины Тьюринга.

Структура машины Тьюринга Машина Тьюринга (МТ) состоит из двух частей - ленты и автомата (рис. 1):

Рисунок 1. Машина Тьюринга.

Лента используется для хранения информации. Она бесконечна в обе стороны и разбита на клетки, которые не имеют нумерацию и имена. В каждой клетке может быть записан один символ или ничего не записано. Содержимое клетки может меняться - в неё можно записать другой символ или стереть находящийся там символ.

Обозначим пустое содержимое клетки символом «пусто» и любым свободным знаком (например Λ или X) .Поэтому изображение ленты, показанное на рисунке 1 справа, такое же, как и на рисунке 1 слева. Удобно операцию стирания символа в некоторой клетке рассматривать как запись в эту клетку символа X.

Автомат - это активная часть МТ. В каждый момент он размещается под одной из клеток ленты и видит её содержимое; это видимая клетка, а находящийся в ней символ - видимый символ; содержимое соседних и других клеток автомат не видит. Кроме того, в каждый момент автомат находится в одном из состояний q1, q2 и т.п. Находясь в некотором состоянии, автомат выполняет какую-то определённую операцию (например, перемещается направо по ленте, заменяя все символы b на a), находясь в другом состоянии - другую операцию.

Пару из видимого символа (S) и текущего состояния автомата (q) будем называть конфигурацией и обозначать <S, q>.

Автомат может выполнять три элементарных действия:

1) записывать в видимую клетку новый символ (менять содержимое других клеток автомат не может);

2) сдвигаться на одну клетку влево или вправо («перепрыгивать» сразу через несколько клеток автомат не может);

3) переходить в новое состояние.

Кроме трех элементарных действий автомат больше ничего не умеет, поэтому все сложные операции должны быть сведены к этим трём действиям.

Машина Тьюринга работает тактами, которые выполняются один за другим. На каждом такте автомат МТ выполняет три следующих действия, причем обязательно в указанном порядке:

1) записывает некоторый символ S' в видимую клетку (в частности, может быть записан тот же символ, что и был в ней, тогда содержимое этой клетки не меняется);

2) сдвигается на одну клетку влево (обозначение – L (left), либо на одну клетку вправо (обозначение – R( right)), либо остается неподвижным (обозна­чение – “0”).

3) переходит в некоторое состояние q' (в частности, может остаться в преж­нем состоянии).

Формально действия одного такта будем записывать в виде тройки:

S' [L, R, 0], q'

где конструкция с квадратными скобками означает возможность записи в этом месте любой из букв L, Rили N. Например, такт *,L,q8 означает запись симво­ла * в видимую клетку, сдвиг на одну клетку влево и переход в состояние q8.

Для того чтобы заставить машину Тьюринга работать, надо написать для неё программу. Эта программа записывается в виде следующей таблицы 1:

	Si	S2		Si		Sn	X
qi
qi				S', [L, R, 0], q'
qm

Таблица 1. Программа машины Тьюринга

Слева перечисляются все состояния, в которых может находиться автомат, сверху - все символы (в том числе и X), которые автомат может видеть на ленте. (Какие именно символы и состояния указывать в таблице - определяет программист.)

В ячейках таблицы указываются те такты, которые должен выполнить автомат, когда он находится в соответст­вующем состоянии и видит на ленте соответствующий символ.

В целом таблица определяет действия МТ при всех возможных конфи­гурациях и тем самым полностью задаёт поведение МТ.

Описать алгоритм в виде МТ - значит предъявить такую таблицу.

До выполнения программы нужно проделать следующие предварительные действия.

1. записать на ленту входное слово - это конечная последовательность символов, записанных в соседних клетках ленты; внутри входного слова пустых клеток быть не должно, а слева и справа от него должны быть только пустые клетки. Пустое входное слово означает, что все клетки ленты пусты.

2. установить автомат в состояние q1 (указанное в таблице первым) и разместить его под первым символом входного слова. Если входное слово пустое, то автомат может смотреть в любую клетку, т.к. все они пусты.

После этих предварительных действий начинается выполнение программы.

В таблице 1 отыскивается ячейка на пересечении первой строки (т.к. автомат находится в состоянии q1) и того столбца, который соответствует первому символу входного слова (это необязательно левый столбец таблицы), и выполняется такт, указанный в этой ячейке. В результате автомат окажется в новой конфигурации. Теперь такие же действия повторяются, но уже для новой конфигурации:

в таблице 1 отыскивается ячейка, соответствующая состоянию и символу этой конфигурации, и выполняется такт из этой ячейки. И так далее.

Завершается выполнение программы тактом останова - тактом, который ничего не меняет: автомат записывает в видимую клетку тот же символ, что и был в ней раньше, не сдвигается и остается в прежнем состоянии, т.е. это такт S,0,q . Попав на такт останова, МТ, по определению, останавливается, завершая свою работу.

Возможны два исхода работы МТ над входным словом:

1) Первый исход - «хороший»: это когда в какой-то момент МТ останавливается (попадает на такт останова). В таком случае говорят, что МТ применима к задан­ному входному слову. А то слово, которое к этому моменту получено на ленте, считается выходнымм словом, т.е. результатом работы МТ, ответом.

В момент останова должны быть выполнены следующие обязательные условия:

- внутри выходного слова не должно быть пустых клеток (во время выполнения программы внутри обрабатываемого слова пустые клетки могут быть, но в конце их уже не должно остаться);

- автомат обязан остановиться под одним из символов выходного слова (под каким именно - не играет роли), а если слово пустое - под любой клеткой ленты.

2) Второй исход - «плохой»: это когда МТ зацикливается, никогда не попадая на такт останова (например, автомат на каждом шаге сдвигается вправо и потому не может остановиться, т.к. лента бесконечна). В этом случае МТ неприменима к заданному входному слову. Ни о каком результате при таком исходе не может идти и речи.

Один и тот же алгоритм (программа МТ) может быть применимым к одним входным словам (т.е. останавливаться) и неприменимым к другим (т.е. зацикливаться). Таким образом, применимость/неприменимость зависит не только от самого алгоритма, но и от входного слова.

На каких входных словах алгоритм должен останавливаться? На, так сказать, хороших словах, которые относятся к допустимым исходным данным решаемой задачи, для которых задача осмысленна. Но на ленте могут быть записаны любые входные слова, в том числе и те, для которых задача не имеет смысла; на таких словах поведение алгоритма не фиксируется, он может остановиться (при любом результате), а может и зациклиться.

Формально можно считать, что в программе МТ имеется конечное состояние q, во всех ячейках которого записаны такты останова. При этом, однако, такую строку явно не выписывают, а лишь подразумевают.

Рассмотрим пример на составление программы для МТ.

Для сокращения формулировки задач введём следующие два соглашения:

- буквой Р будем обозначать входное слово;

- буквой А будем обозначать алфавит входного слова, т.е. набор тех симво­лов, из которых может состоять Р (отметим, однако, что в промежуточных и выходном словах могут появляться и другие символы).

Задача 1:

Пусть алфавит А={0,1,}, Р - непустое слово (последова­тельность из двоичных цифр), т.е. неотрицательное целое число в двоичной системе. Требуется получить на ленте запись числа, которое на 1 больше числа Р и вернуть головку на начало слова.

Решение:

Для решения этой задачи предлагается выполнить следующие действия:

1. Перегнать автомат на последнюю младшую цифру числа.

2. Если это цифра 0, то заменить её цифрой на 1 и вернуться в исходное положение.

3. Если это цифра 1 , то заменить ее цифрой 0 и сдвинуться влево.

4. Особый случай: в Pтолько единицы (например 11). Тогда автомат будет сдвигаться влево, заменяя единицы на нули, и в конце концов окажется под пустой клеткой. В нее надо записать 1 и остановиться (ответом будет 100)

q1 - это состояние, в котором автомат «бежит» к последней младшей цифре числа.

Для этого он всё время движется вправо, не меняя видимые цифры и оставаясь в том же состоянии. Но когда автомат находится под последней цифрой, то он ещё не знает об этом (он не видит, что записано в соседних клетках) и определит это лишь тогда, когда попадёт на пустую клетку. Поэтому, дойдя до первой пустой клетки, автомат возвращается назад под послед­нюю цифру и переходит в состояние q2(вправо двигаться уже не надо).

q2 - это состояние, в котором автомат прибавляет 1 к той цифре, которую видит в данный момент. Сначала это последняя цифра числа; если она 0, то автомат заменяет её цифрой, которая на 1 больше, и возвращается в исходное положение. Но если это цифра 1, то автомат заменяет её на 0 и сдвигается влево, оставаясь в состоянии q2. Тем самым, он будет теперь прибавлять 1 к предыдущей цифре. Если и эта цифра равна 1, то автомат заменяет её на 0 и сдвигается влево, оставаясь по- прежнему в состоянии q2, т.к. должен выполнить то же самое действие - увеличить на 1 видимую цифру. Если же автомат сдвинулся влево, а в видимой клетке нет цифры (а есть «пусто»), то он записывает сюда 1 и останавливается.

q3 - это состояние, в котором автомат возвращается в исходную позицию,сдвигаясь влево,пока не попадется пустая клетка(начало слова). Далее сдвиг вправо на начало слова.

q4 - это состояние, в котором автомат останавливается.

Отметим, что для пустого входного слова наша задача не определена, поэтому на этом слове МТ может вести себя как угодно. В нашей программе, например, при пустом входном слове МТ останавливается и выдает ответ 1.

Приведем запись программы в полном виде в таблице 2:

алфавит (текущее состояние ячейки)			x
текущее состояние головки	записать в ячейку	состояние головки	движение головки	записать в ячейку	состояние головки	движение головки	записать в ячейку	состояние головки	движение головки
							x		-1
			-1			-1			-1
			-1			-1	x

Таблица 2. Запись программы прибавления единицы к двоичному числу.

Правила выполнения НАМ.

Задается некоторое входное слово Р. Его положение в НАМ не оговаривается.

Работа НАМ сводится к выполнению последовательности шагов. На каждом шаге входящие в НАМ формулы подстановки просматриваются сверху вниз и выбирается первая из формул, применимых к входному слову Р, т.е. самая верхняя из тех, левая часть которых входит в Р. Далее выполняется подстановка согласно найденной формуле. Получается новое слово Р'.

На следующем шаге это слово Р' берется за исходное и к нему приме­няется та же самая процедура, т.е. формулы снова просматриваются сверху вниз начиная с самой верхней и ищется первая формула, применимая к слову Р, после чего выполняется соответствующая подстановка и получается новое слово Р. И так далее:

Р → Р' → Р " →…

На каждом шаге формулы в НАМ всегда просматриваются начиная с самой первой.

Если на очередном шаге была применена обычная формула (α→β), то работа НАМ продолжается.

Если же на очередном шаге была применена заключительная формула

( α!→β), то после её применения работа НАМ прекращается. То слово, которое получилось в этот момент, и есть выходное слово, т.е. результат применения НАМ к входному слову.

Если на очередном шаге к текущему слову неприменима ни одна формула, то и в этом случае работа НАМ прекращается, а выходным словом считается текущее слово.

Таким образом, НАМ останавливается по двум причинам:

1. Была применена заключительная формула.

2. Ни одна из формул не подошла.

То и другое считается «хорошим» окончанием работы НАМ. В обоих случаях говорят, что НАМ применим к входному слову.

Однако может случиться и так, что НАМ никогда не остановится; это происходит, когда на каждом шаге есть применимая формула и эта формула обычная. Тогда говорят, что НАМ неприменим к входному слову. В этом случае ни о каком результате нет и речи.

Пример 2:

Для сокращения формулировки задач используем следующие соглашения:

1. Буквой Р будем обозначать входное слово.

2. Буквой А будем обозначать алфавит входного слова, т.е. набор тех символов, которые и только которые могут входить во входное слово Р (но в процессе выполнения НАМ в обрабатываемых словах могут появляться и другие символы).

Кроме того, в примерах будем справа от формул подстановки указывать их номера. Эти номера не входят в формулы, а нужны для ссылок на формулы при показе пошагового выполнения НАМ.

Дан алфавит А={a,b,c,d}. В слове Р требуется заменить первое вхождение подслова bb на ddd и удалить все вхождения символа с.

Например: abbcabbca → adddabba

Решение:

В НАМ, в отличие от машины Тьюринга, просто реализуются вставки и удаления символов. Вставка новых символов в слово - это замена некоторого подслова на подслово с большим числом символов; например, с помощью формулы bb→ddd два символа будут заменены на три символа. При этом не надо заботиться о том, чтобы предварительно освободить место для дополнительных символов, в НАМ слово раздвигается автома­тически.

Удаление символов - это замена некоторого подслова на подслово с меньшим числом символов; например, удаление символа “с” реализуется формулой с→ (с пустой правой частью). При этом никаких пустых позиций внутри слова не появляется, сжатие слова в НАМ происходит автоматически.

С учётом сказанного задача должна, казалось бы, решаться так:

1. bb → ddd

2. с →

Однако это не так. Проверим этот НАМ на входном слове abbcabbca:

abbcabbca→adddcabbca→adddcadddca→adddadddca→…

Заменив первое вхождение bb на ddd, НАМ не перешёл сразу к удалению символов “c”, а стал заменять и другие вхождения bb. Потому, что на каждом шаге работы НАМ формулы подстановки всегда просматриваются сверху вниз, начиная с первой из них.

Поэтому, пока применима первая формула, она и будет применяться, блокируя доступ к остальным формулам. Этот означает, что в НАМ важен порядок перечисления формул подстановки.

Учтём это и переставим наши две формулы:

1. с →

2. bb → ddd

Проверим этот новый алгоритм на том же входном слове:

abbcabbca → abbabbca → abbabba → adddabba → adddaddda

Итак, НАМ сначала удалил все символы “c” и только затем заменил первое вхождение bb на ddd. Однако НАМ на этом не остановился и стал заменять остальные вхождения bb.

Дело в том, что, пока применима хотя бы одна формула, НАМ продолжает свою работу. Необходимо принудительно остановить НАМ после того, как он заменил первое вхождение bb.

Для этого нужны заключительные формулы подстановки, после применения

которых НАМ останавливается. Следовательно, в нашем алгоритме обычную

формулу bb→ddd надо заменить на заключительную формулу bb!→ddd:

1. с →

2. bb !→ ddd

Теперь алгоритм будет работать правильно:

abbcabbca → abbabbca → abbabba !→ adddabba

Слово, которое получилось после применения заключительной формулы ,

является выходным словом, т.е. результатом применения НАМ к заданному

входному слову.

Проверим наш НАМ ещё и на входном слове, в которое не входит bb:

dcacb → dacb → dab

К последнему слову dab неприменима ни одна формула, поэтому, согласно

определению НАМ, алгоритм останавливается и это слово объявляется выходным.

Пример 3:

Дан алфавит А={a,b}. Удалить из непустого слова Р его первый символ. Пустое слово не менять.

Решение:

Удалив первый символ слова, надо тут же остановиться. Поэтому, казалось бы, задачу решает следующий НАМ:

1. a!→

2. b!→

Однако это неправильный алгоритм, в чём можно убедиться, применив его к слову bbaba:

bbaba → bbba

Как видно, этот НАМ удалил не первый символ слова, а первое вхождение символа. Данный алгоритм будет правильно работать, только если входное слово начинается с символа “а”. Перестановка формул в этом НАМ не поможет, т.к. тогда он будет неправильно работать на словах, начинающихся с “а”.

Надо пометить первый символ слова, поставив перед ним какой-либо знак, скажем “%”, отличный от символов алфавита слова. После этого уже можно с помощью формул вида %Δ !→ заменить этот знак и первый символ Δ слова на пусто и остановиться: bbaba → %bbaba !→ baba

Поставить % перед первым символом МОЖНО формулой →% с пустой левой частью, которая приписывает свою правую часть слева к слову.

Получаем следующий НАМ:

1. →%

2. %a!→

3. %b!→

Проверим его на том же входном слове:

bbaba → %bbaba → %%bbaba → %%%bbaba →… _

Как видно, этот алгоритм постоянно приписывает слева символы “%”.

Формула постановки с пустой левой частью применима всегда, поэтому наша формула будет работать бесконечно, блокируя доступ к ос­тальным формулам. Отсюда вытекает важное правило:

если в НАМ есть формула с пустой левой частью (→β), то её место - только в самом конце НАМ. Учтём это правило и перепишем наш НАМ:

1 %a!→

2 %b!→

3 →%

Проверим данный алгоритм:

bbaba → %bbaba → baba

Алгоритм зациклился на пустом входном слове, т.к. постоянно будет применяться формула 3, а согласно условию задачи на таком слове НАМ должен остановиться. Дело в том, что мы ввели знак % для того, чтобы пометить первый символ слова, а затем уничтожить % и этот символ. Но в пустом слове нет ни одного символа, поэтому формулы 1 и 2 ни разу не сработают и по­стоянно будет выполняться формула 3. Следовательно, чтобы учесть случай пустого входного слова, надо после формул 1 и 2 записать ещё одну фор­мулу, которая уничтожает одиночный символ “%” и останавливает алгоритм:

1. %a!→

2. %b!→

3. %!→

4. →%

Вот теперь получили правильный алгоритм.

Пример 4:

Дан алфавит А={a,b}. Требуется приписать символ “a” к концу слова Р.

Например: bbab →bbaba

Решение:

Формула →a приписывает символ “a” слева к слову P, а не справа. Чтобы приписать “a” справа, надо сначала пометить конец слова. Для этого воспользуемся спецзнаком, который поместим в конец P, а затем заменим его на “а”:

P →…→ P% !→ Pa

Чтобы поместить спецзнак в конец слова необходимо сначала спецзнак % приписать слева к слову P, а затем перегнать спецзнак через все буквы слова:

bbab → %bbab → b%bab → bb%ab → bba%b → bbab%

Перепрыгивание % через любой символ Δ алфавита - это замена пары Δ% на пару %Δ ,которая реали­зуется формулой Δ%→%Δ

С учётом всего сказанного получается следующий НАМ:

1. %a → a %

2. %b → b %

3. % !→a

4. → %

Отметим, что при пустом входном слове этот НАМ сначала введёт %, а затем тут же заменит её на символ “a” и остановится.

Основные понятия условного форматирования.

Условное форматирование – это инструмент электронных таблиц Excel, при помощи которого можно изменить форматирование ячеек (цвет заливки, шрифт, границы) в зависимости от заданного условия, не прибегая к помощи встроенного языка программирования Visual Basic for Applications. Условное форматирование может значительно упростить выделение определенных ячеек или диапазона ячеек и визуализацию данных с помощью гистограммы, цветовых шкал и наборов значков. Оно изменяет внешний вид диапазона ячеек на основе указанного условия (или критерия). Если условие выполняется, то диапазон ячеек форматируется в соответствии с заданным для условия форматом; если условие не выполняется, то диапазон ячеек не форматируется.

Например, можно выделить ячейку с текущей датой; ячейку с числом, входящим в указанный диапазон; ячейка с определенным текстом и т.п.

Условное форматирование позволяет автоматизировать выполнение однообразных операций. Например, необходимо в большой таблице данных закрасить красным цветом все ячейки, значение в которых превышает 100. Обычно это делается установкой фильтра→Больше 100 и отфильтрованные строки закрашиваются. При изменении данных таблицы необходимо повторить фильтрацию таблицы вручную. Если значения этих ячеек формируются при помощи условного форматирования – ячейки будут окрашены красным автоматически всякий раз при изменении данных.

При создании условного форматирования можно ссылаться на другие ячейки только в пределах одного листа; нельзя ссылаться на ячейки других листов одной и той же книги или использовать внешние ссылки на другую книгу;

При изменении цвета заливки ячеек, цвета шрифта, границ, форматирования текста при помощи условного форматирования – изменения, сделанные при помощи стандартного форматирования не будут отображаться в ячейках, форматы которых были изменены условным форматированием.

Условное форматирование позволяет применять форматирование ячеек избирательно или автоматически на основании их значений.

К примеру, можно задать условное форматирование таким образом, чтобы все ячейки с отрицательными значениями закрашивались в красный цвет. Когда вы вводите или меняете значение в ячейке, Excel проверяет его и сравнивает с условиями, заданными в правилах. Если значение отрицательное, фон ячейки закрасится, иначе останется без изменений.

Условное форматирование – это простой способ определить ячейки с ошибочными записями или значениями определённого типа. Вы можете использовать формат (например, красная заливка), чтобы легко идентифицировать определенные ячейки.

При нажатии кнопки Условное форматирование, которая находится в группе Стили вкладки Главная, вы появляется выпадающее меню со следующими опциями:

Правила выделения ячеек открывает дополнительное меню с различными параметрами для определения правил форматирования ячеек, содержащих конкретные значения или находится в определенном диапазоне.

Правила отбора первых и последних значений открывает опции, позволяющие задавать формат ячейкам на основании вхождения их в топ первых или последних элементов.

Гистограмма открывает палитру гистограмм различных цветов, которые вы можете задать для выбранных ячеек, для визуализации значений, содержащихся в этих ячейках.

Цветовые шкалы позволяет задавать двух- и трехцветовые шкалы для цвета фона ячейки на основе ее значения относительно других ячеек в диапазоне

Наборы значков отображает значок в ячейке. Какой именно значок отображается, зависит от значения ячейки относительно других ячеек. Excel предоставляет 20 наборов значков на выбор (при этом вы можете смешивать и сочетать значки из разных наборов). Количество значков в наборах колеблется от трех до пяти.

Создать правило открывает диалоговое окно Создание правила форматирования, которое позволяет создать пользовательское условное форматирование для выбранных ячеек.

Удалить правила открывает дополнительное меню, где вы можете удалить правила условного форматирования как для выбранных ячеек, так и на всем листе.

Управление правилами открывает диалоговое окно Диспетчер правил условного форматирования, которое позволяет редактировать и удалять определенные правила, а также задавать приоритет, передвигая вниз и вверх по списку правил.

Рассмотрим пример создания правила изменения формата ячейки на красную заливку с темно-красным шрифтом при условии, если значение ячейки содержит слово Нет.

Выделим диапазон ячеек, к которому применяется условное форматирование. Переходим по вкладке Главная в группу Стили, щелкаем кнопку Условное форматирование → Правила выделения ячеек → Текст содержит (Рис 3):

В появившемся диалоговом окне Текст, который содержит в левом текстовом поле необходимо задать фрагмент текста, который будет условием для применения формата к ячейке, указанного в правом выпадающем списке. В нашем случае – это Светло-красная заливка и темно-красный текст.

Щелкаем ОК, чтобы наше правило вступило в силу.

Рассмотрим еще один пример:

Применить три различных условных форматирования к одному и тому же диапазону ячеек: первый тип формата, когда ячейка содержит целевое значение, второй – когда больше цели и третий – когда меньше. Желая заливка с темно-желтым текстом для ячеек содержащих значение 95, Зеленая заливка с темно-зеленым текстом для ячеек со значениями больше 95 и Светло-красная заливка и темно-красным текстом для ячеек меньше 95.

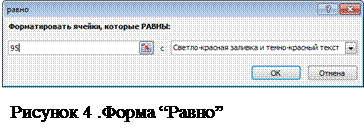Выделяем диапазон ячеек, к которому мы хотим применить три различных правила условного форматирования. Начнем с создания правила для ячеек, содержащих значение равное 95. Переходим по вкладке Главная в группу Стили, щелкаем кнопку Условное форматирование -> Правила выделения ячеек -> Равно (рис 4).

Excel откроет диалоговое окно Равно, где в левом текстовом поле необходимо указать условие 95, а в правом выпадающем списке выбрать формат для этого условия Желтая заливка с темно-желтым текстом.

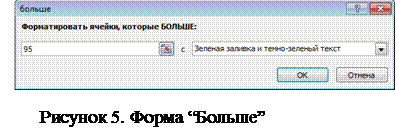
Далее задаем условное форматирование для значений больше 95. Из меню Условное форматирование → Правила выделения ячеек выбираем Больше, в появившемся диалоговом окне Большеуказываем значение, выше которого ячейка будет закрашиваться в зеленый цвет, и сам формат (рис 5).

Аналогичную операцию проделываем для ячеек со значениями меньше 95. На этот раз из списка правил необходимо выбрать Меньше и задать формат с красной заливкой.

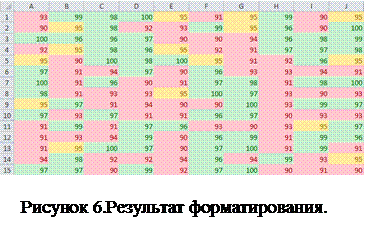По мере того, как вы будете определять все три правила для диапазона, ячейки будут закрашиваться в определенный цвет. В итоге мы получим, примерно такую картину (рис 6).

Обратите внимание, что если ячейка будет пустой, она тоже будет закрашиваться в красный цвет, предполагая, что значение ячейки меньше 95.

Excel предлагает большое количество готовых правил. Но можно задать свое собственное правило на основе формулы. Например, есть таблица с данными по дням и необходимо, чтобы ячейки с выходными днями (суббота и воскресенье) закрашивались.

Выделяем таблицу с данными, к которой мы хотим применить условное форматирование. Переходим по вкладке Главная в группу Стили, щелкаем кнопку Условное форматирование → Создать правило. В появившемся диалоговом окне Создание правила форматирования в поле Выберите тип правила выбираем Использовать формулу для определения форматируемых ячеек.

В поле Измените описание правила задаем условия и формат для нашего правила.

В нашем случае, условием будет формула: =ИЛИ(ДЕНЬНЕД($A2;2)=6;ДЕНЬНЕД($A2;2)=7).

В качестве формата выбираем темно- красную заливку (рис 7).

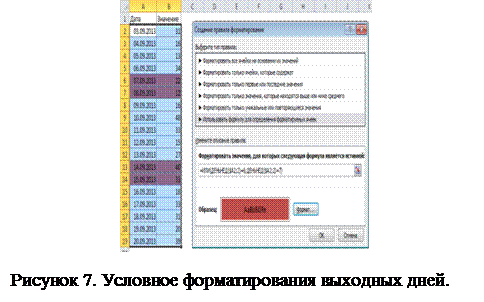
Условное форматирование является полезным инструментом для визуализации числовых данных. В ряде случаев условное форматирование является реальной альтернативой создания диаграммы.

Ход работы.

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образовании

“Ижевский государственный технический университет имени М.Т.Калашникова” (ИжГТУ)

С.Н.Селивановский,

В.П. Тарануха ,

О.Я. Шамсиахметов

МЕТОДИЧЕСКое руководство

к лабораторной работе по курсу ” Информатика”

направления 211000 “Конструирование и технология электронных средств” профиля ”Проектирование и технология радиоэлектронных средств”

Лабораторная работа № 1

Создание имитационных моделей абстрактных автоматов Тьюринга и Маркова средствами Excel MS Office.

Ижевск 2014

СоставителИ: С.Н.селивановский,доцент

в.п.Тарануха, канд.техн.наук, доцент

шАМСИАХМЕТОВ о.я.

Рецензенты - канд. физ.-мат. наук, доцент Клишин С.В.,

доктор техн. наук, профессор ушаков П.А.

МЕТОДИЧЕСКОЕ РУКОВОДСТВО к лабораторной работе №1 “ Создание имитационных моделей абстрактных автоматов Тьюринга и Маркова средствами Excel MS Office.

. ” пО курсу ” ИНФОРМАТИКА” профиля ”Проектирование и технология радиоэлектронных средств”/ сЕЛИВАНОВСКИЙ с.н.,Тарануха В.П.,ШАМСИАХМЕТОВ О.Я.-: Ижевск: Издательство ИжГТУ, 2014.- 46 с.

Настоящие методические указания определяют последователь­ность выполнения лабораторной работы по дисциплине «ИНФОРМАТИКА» и включают в себя рекомендации ПО СОЗДАНИЮ ПРИКЛАДНЫХ ПРОГРАММ имитационных моделей абстрактных автоматов, А ТАКЖЕ МЕТОДЫ адаптации программного обеспечения к конкретным задачам оптимизации алгоритмов.

© СЕЛИВАНОВСКИЙ С.Н.,Тарануха В.П.,шамсиахметов О.Я.

© ИжГТУ, 2014

Краткая теория.

Описание машины Тьюринга.

Структура машины Тьюринга Машина Тьюринга (МТ) состоит из двух частей - ленты и автомата (рис. 1):

Рисунок 1. Машина Тьюринга.

Лента используется для хранения информации. Она бесконечна в обе стороны и разбита на клетки, которые не имеют нумерацию и имена. В каждой клетке может быть записан один символ или ничего не записано. Содержимое клетки может меняться - в неё можно записать другой символ или стереть находящийся там символ.

Обозначим пустое содержимое клетки символом «пусто» и любым свободным знаком (например Λ или X) .Поэтому изображение ленты, показанное на рисунке 1 справа, такое же, как и на рисунке 1 слева. Удобно операцию стирания символа в некоторой клетке рассматривать как запись в эту клетку символа X.

Автомат - это активная часть МТ. В каждый момент он размещается под одной из клеток ленты и видит её содержимое; это видимая клетка, а находящийся в ней символ - видимый символ; содержимое соседних и других клеток автомат не видит. Кроме того, в каждый момент автомат находится в одном из состояний q1, q2 и т.п. Находясь в некотором состоянии, автомат выполняет какую-то определённую операцию (например, перемещается направо по ленте, заменяя все символы b на a), находясь в другом состоянии - другую операцию.

Пару из видимого символа (S) и текущего состояния автомата (q) будем называть конфигурацией и обозначать <S, q>.

Автомат может выполнять три элементарных действия:

1) записывать в видимую клетку новый символ (менять содержимое других клеток автомат не может);

2) сдвигаться на одну клетку влево или вправо («перепрыгивать» сразу через несколько клеток автомат не может);

3) переходить в новое состояние.

Кроме трех элементарных действий автомат больше ничего не умеет, поэтому все сложные операции должны быть сведены к этим трём действиям.

Машина Тьюринга работает тактами, которые выполняются один за другим. На каждом такте автомат МТ выполняет три следующих действия, причем обязательно в указанном порядке:

1) записывает некоторый символ S' в видимую клетку (в частности, может быть записан тот же символ, что и был в ней, тогда содержимое этой клетки не меняется);

2) сдвигается на одну клетку влево (обозначение – L (left), либо на одну клетку вправо (обозначение – R( right)), либо остается неподвижным (обозна­чение – “0”).

3) переходит в некоторое состояние q' (в частности, может остаться в преж­нем состоянии).

Формально действия одного такта будем записывать в виде тройки:

S' [L, R, 0], q'

где конструкция с квадратными скобками означает возможность записи в этом месте любой из букв L, R