Общая характеристика умозаключений
УМОЗАКЛЮЧЕНИЕ
Общая характеристика умозаключений
Умозаключение – форма мышления, в которой из одного или нескольких суждений, называемых посылками (основаниями), выводится новое суждение, называемое заключением или следствием, выводом.
Структура любого умозаключения включает посылки (два первые суждения в примере), заключение (третье суждение) и логическую связь между посылками и заключением.
Логическая связь выражается опосредованно, через используемые логические правила вывода.
Все умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии.
Дедуктивные умозаключения
Дедуктивные умозаключения – вид умозаключений, в котором из посылок, выражающих знания большей степени общности, необходимо следует заключение, выражающее знание меньшей степени общности. Дедукция в переводе с латинского означает "выведение".
Примеры: "Ни один смертный не может до конца постичь замысел Бога. Все люди смертны. Ни один человек не может до конца понять замысел Бога".
Виды дедуктивных умозаключений
Все дедуктивные умозаключения делятся на непосредственные умозаключения и силлогизмы – умозаключения, в которых из двух суждений выводится третье.
Силлогизмы, в свою очередь, делятся по характеру составляющих их суждений на категорический, условный, разделительный и их комбинации: условно-категорический, разделительно-категорический и условно-разделительный силлогизмы. По составу и полноте речевого выражения выделяют простые, сложные, сокращённые и сложносокращённые силлогизмы.
Простой категорический силлогизм
Категорический силлогизм – вид дедуктивного умозаключения, в котором из двух истинных категорических суждений, связанных средним термином, при соблюдении правил вывода необходимо следует заключение.
Понятия, входящие в состав силлогизма, называются терминами силлогизма. В простом категорическом силлогизме только 3 термина:
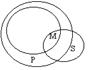
больший термин (Р) – предикат заключения;
меньший термин (S) – субъект заключения;
средний термин (М) – связывает в посылках Р и S, в заключении отсутствует.
Структуру простого категорического силлогизма составляют две посылки и заключение. Посылка, содержащая больший термин (Р), называется большей посылкой; посылка, содержащая меньший термин (S) – меньшей посылкой.
| Все жидкости (М) – упруги (Р) – большая посылка Ртуть (S) – жидкость (М) – меньшая посылка Ртуть (S) – упруга (Р) – заключение |
Общие правила простого категорического силлогизма
Правила терминов
1. В силлогизме должно быть только три термина (S, P, M). Нарушение этого правила ведёт к ошибке "учетверение терминов":
| Движение (М) – вечно (Р) |
| Хождение в школу (S) – движение (М) |
| Хождение в школу вечно |
В данном силлогизме средний термин "движение" употребляется в разных смыслах – в предельно широком (философском) и обыденном (движение как перемещение). Заключение ложно.
2. Средний термин должен быть распределён по крайней мере в одной из посылок.
| Все гусеницы (Р) едят салат (М) |
| Я (S) ем салат (М) |
| Я – гусеница |
Средний термин (те, кто едят салат) не распределён ни в одной из посылок. Вывод ложный.
3. Термин в заключении может быть распределён только тогда, когда он распределён в посылке.
| Во всех городах за полярным кругом (М) – белые ночи (Р) |
| Санкт-Петербург (S) – не за полярным кругом (М) |
| В Санкт-Петербурге не бывает белых ночей. |
Предикат вывода распределён в заключении, но не распределён в посылке. В терминах заключения говорится больше, чем в посылках: произошло расширение большего термина. Заключение ложно.
Правила посылок
1. Из двух отрицательных посылок вывод не производится.
| Дельфины не рыбы. |
| Щуки не дельфины. |
| ? |
2. Если одна из посылок отрицательная, то и заключение должно быть отрицательным:
| Некоторые люди не умеют читать. |
| Все люди умеют смеяться. |
| Некоторые из умеющих смеяться не умеют читать. |
3. Из двух частных посылок нельзя сделать вывод:
| Некоторые животные живут в воде. |
| Некоторые говорящие существа – животные. |
| ? |
4. Если одна из посылок частная, то заключение должно быть частным:
| Все люди обладают сознанием. |
| Некоторые двуногие существа – люди. |
| Некоторые двуногие существа обладают сознанием. |
Условные умозаключения
Чисто условный силлогизм – умозаключение, в котором обе посылки являются условными суждениями.
| Если а, то b | а -> b |
| Если b, то c | b -> с |
| Если а, то с | а -> с |
Пример: Если сложить 2 нечётных числа, то их сумма будет чётным числом; если их сумма – чётное число, то она будет делиться пополам без остатка. Значит, если сложить 2 нечётных числа, то их сумма будет делиться пополам без остатка.
Это отношение суждений выражается формулой: следствие следствия есть следствие основания.
Условно-категорический силлогизм – умозаключение, в котором одна посылка – условное суждение, а другая посылка и вывод – категорические суждения.
Этот силлогизм имеет два правильных модуса: утверждающий и отрицающий.
1. Утверждающий модус (modus ponens) выражается формулой:

Если во второй посылке утверждается следствие первой посылки, то вывод может быть только вероятным.
Примеры:

Если идёт дождь, прохожие раскрывают зонты.
Прохожие раскрывают зонты.
Вероятно, идёт дождь.
2. Отрицательный модус (modus tollens):
Примеры:
| Если на улице светит солнце, то предметы отбрасывают тень. Предметы не отбрасывают тень. На улице не солнечно. | а ->b b а |
Если отрицается основание условной посылки, то вывод может быть только вероятным.
Примеры:
| Если число делится на четыре, то оно делится на два. Число не делится на четыре. Вероятно, оно не делится на два. | а -> b а вероятно, b |
Разделительный силлогизм
Чисто разделительный силлогизм состоит только из разделительных посылок, и вывод – тоже разделительное суждение.
Пример:
Все тела делятся на твёрдые, жидкие и газообразные.
Твёрдые тела бывают тугоплавкими и легкоплавкими.
Все тела либо твёрдые тугоплавкие, либо твёрдые
легкоплавкие, либо жидкие, либо газообразные.
S есть А, или В, или С
А есть А1, или А2
S есть А1, или А2, или В, или C
По сути, такое умозаключение даёт увеличение количества альтернатив, углубляет дизъюнкцию.
В рассуждениях гораздо большее значение имеет разделительно-категорический силлогизм, в котором одна посылка – разделительное суждение, а другая – простое категорическое суждение. Разделительно-категорический силлогизм имеет два правильных модуса.
1. Утверждающе-отрицающий модус (modus ponendo tollens):
Разделительная посылка – дизъюнкция альтернатив. Категорическая посылка – утверждение одной из альтернатив. Заключение – категорическое суждение, отрицающее другую (другие) альтернативу.
Пример:
| Больной либо жив, либо мёртв. Больной ещё жив. Значит, он не умер. | а v b а b | а v b b а |
Необходимым условием правильности вывода по этому модусу является строгость дизъюнкции альтернатив (соединение их союзом "либо"). В случае нестрогой дизъюнкции ("или") вывод с необходимостью не следует.
Пример:
Или ты меня не понял, или я тебя не понял.
Я тебя не понимаю.
? Возможно, оба не поняли друг друга.
2. Отрицающе-утверждающий модус (modus tollendo ponens):
| а v b а b | а v b b а | а v b а b | а v b b а |
В этом модусе правильный вывод возможен при строгой и при нестрогой дизъюнкции разделительной посылки. Необходимым условием правильности вывода по этому модусу является перечисление в разделительной посылке всех возможных альтернатив.
Примеры:
Смерть могла наступить в результате
убийства или самоубийства.
Это не самоубийство.
Следовательно, смерть наступила в результате убийства.
В данном примере не учтена возможность, например, несчастного случая.
Правонарушение может быть проступком либо преступлением.
Это не преступление
Следовательно, это проступок.
Ученики должны решить задачу в классе или дома.
В классе задачу решить не успели.
Ученики должны решить задачу дома.
Индуктивные умозаключения
Индуктивные умозаключения имеют иную логическую природу, нежели дедуктивные. Дедукция, обеспечивая достоверные выводы из истинных посылок, не даёт знания, выходящего за рамки знания, содержащегося в этих посылках. Индукция (в переводе с латинского – "наведение") всегда выходит на новое, не содержащееся в посылках знание, достоверность которого носит вероятностный характер.
В основе логического перехода от посылок к заключению в индуктивном умозаключении лежит подтверждённое практикой положение о всеобщем характере причинной связи, о проявлении необходимых признаков предметов и явлений через их устойчивую повторяемость. Индукция – это переход от знания меньшей степени общности к более общему знанию.
Индуктивное умозаключение – умозаключение, в котором на основании принадлежности признака отдельным предметам делают вывод о его принадлежности классу предметов в целом.
Пример:
Меркурий движется вокруг Солнца.
Земля движется вокруг Солнца.
Венера движется вокруг Солнца.
Марс движется вокруг Солнца.
Сатурн движется вокруг Солнца.
Юпитер движется вокруг Солнца.
Уран движется вокруг Солнца.
Нептун движется вокруг Солнца.
Плутон движется вокруг Солнца.
Меркурий, Земля, Венера, Марс, Сатурн, Юпитер, Уран,
Нептун, Плутон – все известные планеты Солнечной системы.
Все известные планеты Солнечной системы движутся вокруг Солнца.
Степень достоверности индуктивного умозаключения зависит от законченности и полноты опытного исследования. Различают два вида индуктивных умозаключений – полную и неполную индукцию.
Полная индукция
Полная индукция – это умозаключение, в котором на основе принадлежности каждому предмету определённого признака делают вывод о его принадлежности классу предметов в целом.
Полная индукция применяется только тогда, когда исследуется класс с ограниченным числом элементов.
Пример:
Швеция имеет парламент.
Норвегия имеет парламент.
Финляндия имеет парламент.
Швеция, Норвегия, Финляндия – все страны полуострова Скандинавия.
Все страны полуострова Скандинавия имеют парламент.
Информация, выраженная в посылках данного умозаключения о каждом элементе класса, служит показателем полноты исследования и достаточным основанием для логического переноса признака на весь класс. Таким образом, вывод в умозаключении полной индукции является необходимо истинным.
Неполная индукция
Если невозможно охватить исследованием весь класс предметов, то обобщение строится в форме неполной индукции.
Неполная индукция – это умозаключение, в котором на основе принадлежности определённого признака некоторым элементам исследуемого класса делают вывод о его принадлежности всему классу в целом.
Для неполной индукции характерно ослабленное логическое следование – истинные посылки обеспечивают проблематичное заключение.
В подобных выводах получают вероятностное знание.
Пример:
В философии применяется метод индукции.
В физике применяется метод индукции.
В истории применяется метод индукции.
В математике применяется метод индукции.
В биологии применяется метод индукции.
Философия, физика, история, математика, биология – науки.
Индукция – общенаучный метод.
Большое значение в выводах неполной индукции имеет способ отбора исходного материала. По этому критерию различают два вида неполной индукции:
1) популярная индукция (через простое перечисление)
2) научная индукция (путём отбора).
Популярная индукция – вывод, в котором путём перечисления устанавливают принадлежность признака некоторым предметам какого-либо класса и на этой основе проблематично заключают о его принадлежности всему классу. В популярной индукции не исключается возможность ошибочного вывода.
Пример:
Франция имеет конституцию.
Испания имеет конституцию.
Россия имеет конституцию.
Швейцария имеет конституцию.
Франция, Испания, Россия, Швеция – европейские страны.
Все европейские страны имеют конституцию.
Заключение ошибочно, т. к. Англия конституции не имеет.
В Европе, на основе многочисленных наблюдений, считалось истинным суждение "Все лебеди белые", пока в Австралии не обнаружили чёрных лебедей. Суждение оказалось ложным. Подобная ошибка называется "поспешное обобщение" – она вызвана нарушением закона достаточного основания в процессе индуктивного умозаключения (в посылках не учтены все возможные случаи). Возможна ещё одна ошибка "после этого, значит, по причине этого", источник её – смешение причинной связи с простой последовательностью. Построенные с этой ошибкой индуктивные умозаключения породили много суеверий и примет: "чёрная кошка", "дурной глаз", "женщина с пустым ведром" и т.п.
Научная индукция
Научной индукцией называют индуктивное умозаключение, в котором вывод строится путём отбора необходимых признаков и исключения случайных обстоятельств.
В зависимости от способов исследования различают:
(1) индукцию методом отбора (селекции).
(2) индукцию методом исключения (элиминации).
1. Индукция методом отбора – это умозаключение, в котором вывод о принадлежности признака всему классу предметов основывается на знании о подклассе-образце, полученном методическим отбором явлений из различных областей этого класса. Примером подобной индукции может служить вывод о том, что серебро обладает целебными свойствами. На основании многолетних эмпирических наблюдений было заключено, что серебро очищает питьевую воду. Соли серебра стали добавлять в составы при лечении ожогов. Вывод получен на основе индукции методом отбора.
2. Индукция методом исключения – это система умозаключений, в которой вывод о причинах исследуемых явлений строится путём обнаружения подтверждающих обстоятельств и исключения обстоятельств, не удовлетворяющих свойствам причинной связи. Смысл данного типа индукции в установлении причинных связей.
Причинная связь обладает следующими свойствами:
1) всеобщность: каждое явление имеет свою причину; беспричинных явлений не существует;
2) последовательность во времени: причина всегда предшествует следствию (действию);
3) необходимость: отсутствие причины – отсутствие следствия (действия);
4) однозначность: каждая конкретная причина всегда вызывает определённое следствие (действие).
Виды аналогии
В зависимости от характера информации, переносимой с одного предмета на другой, аналогия делится на два вида:
1. Аналогия предметов (свойств) – умозаключение, в котором объектами уподобления выступают два единичных предмета, а переносимым признаком – качества или свойства предметов.
Предмет А обладает свойствами а, b, с, d, e, f.
Предмет В обладает свойствами а, b, с, d, e
Вероятно, предмет В обладает свойствами f.
Рассуждение по аналогии свойств использовал голландский физик ХVII в. Гюйгенс, выявляя природу света. Основываясь на сходстве света и звука в таких свойствах как отражение, преломление, прямолинейное распространение и интерференция, он уподобил световое движение звуковому и пришёл к выводу, что свет также имеет волновую природу.
2. Аналогия отношений – умозаключение, в котором объектом уподобления выступают сходные отношения между двумя парами предметов, а переносимым признаком – свойства этих отношений.
Используя аналогию отношений, Резерфорд предложил планетарную модель атома. Модель построена на основании аналогии отношения между Солнцем и планетами, с одной стороны, и ядром атома и электронами, с другой стороны.
По степени достоверности заключения аналогию делят на три вида:
1. Строгая аналогия. Отличительная её особенность – необходимая связь переносимого признака с признаками сходства. Строгая аналогия даёт достоверное знание.
Предмет А обладает признаками а, b, с, d, e, f.
Предмет В обладает признаками а, b, с, d, e.
Из совокупности признаков а, b, c, d, e необходимо следует f.
Предмет В обязательно обладает признаками f.
Строгую аналогию используют в математических доказательствах, научных исследованиях. Примером строгой аналогии является пропорция.
2. Нестрогая аналогия. Связь между сходными и переносимыми признаками мыслится как необходимая лишь с большей или меньшей степенью вероятности. Используется в исторических исследованиях, при испытаниях моделей.
Предмет А обладает признаками а, b, c, d, e, f.
Предмет В обладает признаками а, b, с.
Вероятно, предмет В обладает признаками f.
Степень вероятности заключений по нестрогой аналогии можно повысить, если соблюдаются следующие условия:
а) число общих признаков должно быть по возможности большим;
б) сходные признаки должны быть существенными;
в) общие признаки должны быть по возможности более разнородными;
г) необходимо учитывать количество и существенность пунктов различия;
д) переносимый признак должен быть того же типа, что и сходные признаки.
3. Поверхностная (ложная) аналогия. Когда у сравниваемых предметов обнаружено недостаточное число сходных признаков или когда зависимость между сходными и переносимыми признаками установлена в слабой форме, если не учитываются признаки различия, тогда перед нами поверхностная (ложная) аналогия. Истинное заключение в таком выводе может быть лишь случайным.
Пример:
Наполеон был маленького роста, носил сапоги и мундир, был военным гением.
Я – маленького роста, ношу сапоги и мундир.
Я – военный гений.
В этом умозаключении недостаточное число сходных признаков, сходные признаки несущественны, не учтены различия и их существенность, переносимый и сходные признаки разнородны, аналогия, в лучшем случае, случайна.
УМОЗАКЛЮЧЕНИЕ
Общая характеристика умозаключений
Умозаключение – форма мышления, в которой из одного или нескольких суждений, называемых посылками (основаниями), выводится новое суждение, называемое заключением или следствием, выводом.

Структура любого умозаключения включает посылки (два первые суждения в примере), заключение (третье суждение) и логическую связь между посылками и заключением.
Логическая связь выражается опосредованно, через используемые логические правила вывода.
Все умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии.
Дедуктивные умозаключения
Дедуктивные умозаключения – вид умозаключений, в котором из посылок, выражающих знания большей степени общности, необходимо следует заключение, выражающее знание меньшей степени общности. Дедукция в переводе с латинского означает "выведение".
Примеры: "Ни один смертный не может до конца постичь замысел Бога. Все люди смертны. Ни один человек не может до конца понять замысел Бога".
Виды дедуктивных умозаключений
Все дедуктивные умозаключения делятся на непосредственные умозаключения и силлогизмы – умозаключения, в которых из двух суждений выводится третье.
Силлогизмы, в свою очередь, делятся по характеру составляющих их суждений на категорический, условный, разделительный и их комбинации: условно-категорический, разделительно-категорический и условно-разделительный силлогизмы. По составу и полноте речевого выражения выделяют простые, сложные, сокращённые и сложносокращённые силлогизмы.
