Конечный автомат. Язык, допускаемый конечным автоматом

Опр. Конечный автомат (ДКА) - набор (Q, S, j, 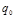, 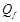), где

Q - конечное множество (внутренних) состояний автомата;

S - конечное множество (входных) символов, «алфавит»;

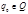- начальное состояние;

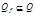- множество заключительных состояний;

j - функция переходов (всюду определенная):

.

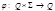(Q, S, j, , )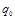

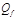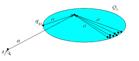
Опр. (как механическое устройство). Конечный автомат состоит из управляющего устройства (УУ), и ленты, разбитой на ячейки.

В каждый момент УУ находится в каком-нибудь состоянии из множества Q, и просматривает ячейку, в которой записан какой-нибудь символ из множества S.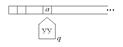

Автомат работает тактами.

На каждом такте, находясь в состоянии q и просматривая ячейку с символом a, автомат выполняет следующие действия:

УУ переходит в состояние q¢, где ;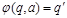

УУ сдвигается по ленте вправо.

Автомат начинает работу в состоянии 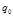(начальное состояние), просматривая самую первую слева ячейку.

Способы задания автомата:

1. Расширенная таблица переходов.

		символы алфавита S
			¼	a	¼	заключ.
состояния из Q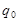
¼
q			j(q, a)		0 или 1

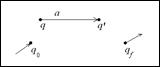
2. Диаграмма переходов.

Пример: «Автомат для продажи кофе».

Пусть стоимость стакана кофе 10 рублей.

Автомат принимает монеты 5 и 10 рублей, S = {5, 10}.

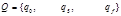
«ожидание клиента»

«кредит 5 рублей»

«кофе»

Расширенная таблица переходов.

			заключ.

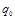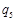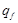Пример: «Автомат для продажи кофе».

Пусть стоимость стакана кофе 10 рублей.

Автомат принимает монеты 5 и 10 рублей, S = {5, 10}.

«ожидание клиента»

«кредит 5 рублей»

«кофе»

Расширенная таблица переходов.

			заключ.

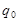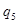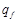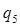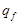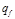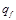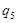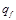Диаграмма переходов:

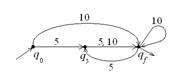
Опр. Автомат допускает слово 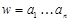, если существует последовательность состояний : , , , …, .

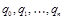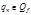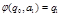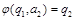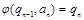(т.е. просмотрев все буквы слова w автомат переходит из начального состояния в заключительное)

Замечание: автомат допускает пустое слово, если .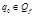

Опр. Язык, допускаемый автоматом - множество всех слов, допускаемых автоматом.

Пример.

Для автомата, продающего кофе, язык L = {5 5, 10, 5 10, 10 10, …}.

Регулярные языки. Теорема Клини

Обозначим 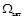класс всех языков над фиксированным алфавитом S, допускаемых конечными автоматами.

Проблема - дать характеристику класса 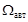, относительно операций над языками.

Теорема.

Класс 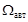замкнут относительно операций пересечения, объединения, дополнения, произведения, итерации.

Теорема.

Класс 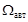замкнут относительно операций пересечения, объединения, дополнения, произведения, итерации.

Доказательство:

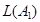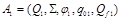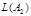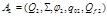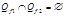Пусть - язык, допускаемый ДКА , - язык, допускаемый ДКА , и . Очевидно, , .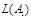

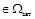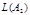
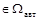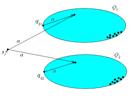
1. Покажем, что .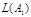

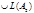
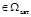Построим НДА 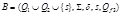, где ,

.

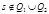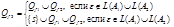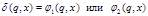, для ; .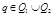

.

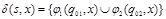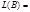
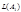
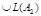По теореме из §4, существует ДКА, допускающий тот же язык.

2. Покажем, что .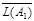

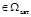Построим ДКА .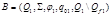

Рассмотрев любое слово w автомат переходит в какое-нибудь состояние q.

Если 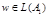, т.е. 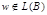, то 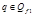, т.е. не является заключительным в автомате В.

И наоборот, если 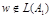, т.е. 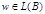, то ,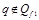

т.е. является заключительным в автомате В.

Следовательно, .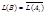

3. .

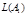
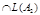
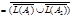4. Покажем, что .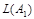

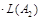
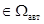1 случай) 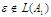, т.е. .

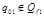Построим НДА 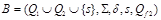, где ,

;

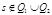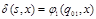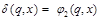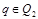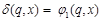, для ;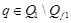

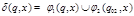, для ; , для .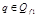

.

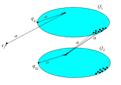
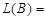
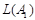
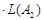По теореме из §4, существует ДКА, допускающий тот же язык.

2 случай) 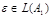, т.е. .

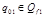К автомату B из случая 1 добавим

.

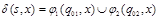
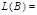
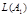
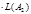По теореме из §4, существует ДКА, допускающий тот же язык.

5. Покажем, что .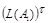

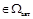Построим НДА 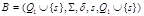, где ,

;

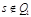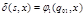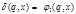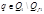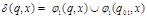, для ;

, для .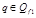

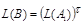
По теореме из §4, существует ДКА, допускающий тот же язык.

Следствие.

Любой конечный язык допускается конечным автоматом.

Доказательство:

Конечный язык - конечное множество слов конечной длины.

1.Если язык пустой (т.е. пустое множество), то он допускается любым ДКА с пустым множеством 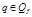заключительных состояний.

2. Если язык состоит из одного пустого слова, то он допускается

ДКА 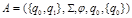, где

, .

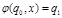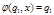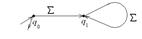
2. Если язык состоит из одного не пустого слова 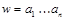, то он допускается НДА 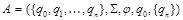, где

, …, .

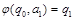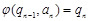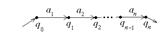
По теореме из §4, существует ДКА, допускающий тот же язык.

4. Если язык 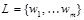, то .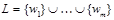

Каждый язык 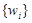допускается ДКА.

Объединение языков допускается автоматом, упоминавшимся в доказательстве теоремы о замкнутости.

Опр. Язык называется регулярным, если он получается из конечных языков применением операций объединения, произведения, итерации.

Обозначим 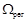класс всех регулярных языков над фиксированным алфавитом S.

Теорема (Клини).

= .

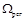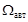Замечание:

Для описания регулярного языка используется регулярное выражение без фигурных скобок.

Например. Для 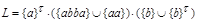используется 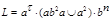или 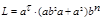.