Арифметика в обратном и дополнительном кодах
Рассмотренные арифметические операции над двоичными числами могут быть сведены к выполнению лишь двух операций; сложения и сдвига. Для этой цели в ЭВМ применяются специальные коды: прямой, обратный и дополнительный.
Для обозначения знака числа, участвующего в операции, в этих кодах выделяется специальный знаковый разряд, в котором записывается 0 для положительного числа и 1 — для отрицательного. Знаковый разряд всегда располагается слева от цифровых разрядов, представляющих данное число.
Прямой код хпр двоичного числа х содержит цифровые разряды этого числа, слева от которых записывается знаковый разряд. Например, для числа х = + 1011 прямой код будет хпр = 0.1011, а для числа х = – 1011 прямой код хпр = 1.1011.
Использование обратного и дополнительного кодов позволяет свести операцию вычитания (алгебраического сложения) чисел к простому арифметическому сложению. Записи положительных чисел в обратном и дополнительном кодах совпадают с их соответствующими записями в прямом коде. Для рассмотренного ранее примера х = + 1011 имеем:
хпр = хобр = хдоп = 0.1011.
Отрицательные числа в этих кодах представляются по-разному.
Обратный код хобр отрицательного числа x получается из прямого кода путем замены значений цифровых разрядов на противоположные. В знаковом разряде, как в прямом коде отрицательного числа, записывается 1. Например, если
x = – 1011, то хпр = 1.1011; хобр = 1.0100.
Дополнительный код хдоп отрицательного числа x образуется из его обратного кода хобр путем прибавления 1 к младшему цифровому разряду. Для предыдущего примера: хобр = 1.0100; хдоп = 1.0101.
В процессе прибавления 1 к младшему разряду могут возникнуть переносы из данного разряда в следующий. Если эта 1 переноса достигает знакового разряда и вызывает соответствующий перенос из него, то при использовании дополнительного кода последний перенос отбрасывается, а при использовании обратного кода единица знакового переноса суммируется с младшим разрядом полученной суммы. Результат вычислений получается в том коде, в каком были представлены слагаемые. Например,
| десятичный код: | обратный код: | дополнительный код: | |||
| – | + | 0.1100 | + | 0.1100 | |
| 1.1010 | 1.1011 | ||||
| 1 0.0110 | 1 0.0111 | ||||
  |   | ||||
| 0.0111 | 0.0111 |
В процессе выполнения расчетов на ЭВМ может образоваться как «положительный», так и «отрицательный» нуль, причем только в дополнительном коде он имеет единственное представление. Действительно,
| в прямом коде: | |
| (+ 0)пр = 0.00...00; | (– 0)пр = 1.00...00; |
| в обратном коде: | |
| (+ 0)обр = 0.00...00; | (– 0)обр = 1.11...11; |
| в дополнительном коде: | |
| (+ 0)доп = 0.00...00; | (– 0)доп = 0.00...00. |
По этой причине, в частности, для представления отрицательных чисел в ЭВМ обычно используется дополнительный код. Поскольку дополнительный код положительного числа совпадает с прямым кодом, то положительные числа участвуют в операциях по сути дела в прямом коде. Как уже отмечалось, использование дополнительных кодов для отрицательных чисел позволяет свести операцию вычитания (или алгебраического сложения) к простому арифметическому суммированию кодов, включая их знаковые разряды. Если в результате суммирования получается положительное число (0 в знаковом разряде), то оно представлено в прямом коде, а если отрицательное число (1 в знаковом разряде), то — в дополнительном коде.
Упражнения
Выполнить арифметические операции со следующими десятичными числами, используя метод дополнительного кода:
а) 7 + 1; б) 31 + 26; в) 8 – 5; г) 89 – 46; д) 1 – 6; е) 20 – 60;
ж) – 3 – 4; з) – 13 – 41; и) 7 – 2; к) 113 – 50; л) 3 – 8; м) 12 – 63.
МАТЕМАТИЧЕСКАЯ ЛОГИКА
Любая, даже самая примитивная ЭВМ — сложнейшее техническое устройство. Но даже такое сложное устройство, как и все в природе и в технике, состоит их простейших элементов. Все устройства ЭВМ состоят из десятков и сотен тысяч элементарных логических схем, так называемых вентилей, объединяемых по правилам и законам (аксиомам) алгебры логики в схемы и модули.
Автором алгебры логики является английский математик Джордж Буль. Занимаясь исследованием законов мышления, он применил в логике систему формальных обозначений и правил, близкую к математической. Впоследствии эту систему назвали логической алгеброй или булевой алгеброй. Правила этой системы применимы к самым разнообразным объектам и их группам (множествам, по терминологии автора). Основное назначение системы Буля состояло в том, чтобы кодировать логические высказывания и сводить структуры умозаключений к простым выражениям, близким по форме к математическим формулировкам. Результатом формального расчета логического выражения является одна из двух логических констант: истина или ложь.
Значение логической алгебры долгое время игнорировалось, поскольку ее приемы и методы не содержали практической пользы для науки и техники того времени. Однако, когда появилась принципиальная возможность создания средств вычислительной техники на электронной базе, операции введенные Булем, оказались весьма полезны. Они изначально ориентированы на работу только с двумя понятиями: истинности и ложности высказывания. Нетрудно понять, как они пригодились для работы с двоичным кодом, который в современных компьютерах тоже представляется всего двумя сигналами: 0 и 1.
Под высказыванием понимается повествовательное предложение, в котором что-либо утверждается или отрицается. В соответствии с такой двоичной природой высказываний условились называть их логическими двоичными переменными и обозначать «1» в случае истинности и «0» в случае ложности. Примерами логических переменных являются высказывания: X = «5 – это четное число», Y = «Квадрат – это геометрическая фигура». На основании этих высказываний можно записать X = 0, Y = 1, так как высказывание X ложно, а высказывание Y истинно.
Высказывания могут быть простыми и сложными: простые содержат одно законченное утверждение, сложные образуются из двух или большего числа простых высказываний, связанных между собой некоторыми логическими связями. Формализация и преобразование связей между логическими переменными осуществляются в соответствии с правилами алгебры логики.
Высказывания строятся над множеством {B, Ø, Ù, Ú, 0, 1}, где B — непустое множество, над элементами которого определены три операции: Ø — отрицание (НЕ), Ù — конъюнкция (И), Ú — дизъюнкция (ИЛИ), а также две константы — логический ноль 0 и логическая единица 1.
Отрицание (инверсия). В русском языке логической операции отрицание соответствует частица НЕ (в некоторых высказываниях применяется оборот «неверно, что…»). Отрицание — унарная (одноместная) операция. Записывается в виде: Ø X или 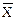 .
.
Конъюнкция (логическое умножение). В русском языке она выражается союзом И. В математической логике используются знаки Ù, & или ´. Конъюнкция — бинарная (двухместная) операция. Записывается в виде: X Ù Y, X & Y или X ´ Y. Значение такого выражения будет Ложь, если значение хотя бы одного из операндов ложно.
Дизъюнкция (логическое сложение). В русском языке она выражается союзом ИЛИ. В математической логике используются знаки Ú или +. Дизъюнкция — бинарная операция. Записывается в виде: X Ú Y или X + Y. Значение такого выражения будет Истина, если значение хотя бы одного из операндов истинно.
Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов: B = {0 (Ложь), 1 (Истина)}. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений, представленных в таблице, однако все они могут быть получены через суперпозицию трёх выбранных операций.
| Функции и их обозначение | Аргументы | Название функции | |||||
| X | Y | X | Y | X | Y | X | Y |
| f1 (XÙY) | Конъюнкция (логическое И) | ||||||
| f2 (XÚY) | Дизъюнкция (логическое ИЛИ) | ||||||
| f3 (XºY) | Эквивалентность | ||||||
| f4 (XÅY) | Сумма по модулю 2 | ||||||
| f5 (XÌY) | Импликация от y к x | ||||||
| f6 (XÉY) | Импликация от x к y | ||||||
| f7 (X¯Y) | Стрелка Пирса («антидизъюнкция») | ||||||
| f8 (X½Y) | Штрих Шеффера («антиконъюнкция») | ||||||
| f9 (XDY) | Инверсия импликации f5 | ||||||
| f10 (YDX) | Инверсия импликации f6 | ||||||
f11 ( 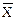 ) ) | Отрицание Х | ||||||
f12 ( 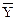 ) ) | Отрицание Y | ||||||
| f13 (X) | Переменная Х | ||||||
| f14 (Y) | Переменная Y | ||||||
| f15 (1) | Константа 1 | ||||||
| f16 (0) | Константа 0 |
Логическая функция (логическое выражение) — формула, содержащая только логические величины и знаки логических операций. Результатом вычисления логической функции является Истина или Ложь.
Не вся система Буля (как и не все предложенные им логические операции) были использованы при создании электронных вычислительных машин. Наибольший практический интерес представляют функции отрицания, логического умножения и логического сложения.
Логическое отрицание НЕ переменной X есть логическая функция F, которая истинна только тогда, когда переменная X имеет значение Ложь, и наоборот.
В алгебре логики любые функции удобно изображать в виде таблицы соответствия всех возможных комбинаций входных логических переменных и выходной логической функции. Для функции логического отрицания НЕ эта таблица имеет вид:
| X | F |
Графически эта функция обозначается кружком на входе или выходе логического символа (рис. 1).
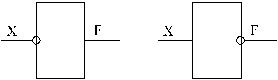
Рис. 1. Графическое изображение функции логического отрицания НЕ
Логическое умножение И двух переменных X и Y есть логическая функция F, которая истинна тогда и только тогда, когда одновременно истинны входные переменные. Для функции логического умножения И таблица истинности имеет вид:
| X | Y | F |
Графическое изображение функции логического умножения И представлено на рис. 2.
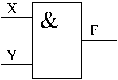
Рис. 2. Графическое изображение функции И
Логическое сложение ИЛИ двух переменных X и Y есть логическая функция F, которая истинна, когда хотя бы одна из входных переменных истинна. Для функции логического сложения ИЛИ таблица соответствия имеет вид:
| X | Y | F |
На рис. 3 представлено графическое изображение функции логического сложения ИЛИ.
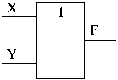
Рис. 3. Условно-графическое изображение функции логической суммы
Три рассмотренные функции позволяют реализовать любую логическую зависимость, они лежат в основе базовых схемотехнических элементов.
Базисом называется совокупность элементов, с помощью которых схемотехнически можно реализовать устройство любой сложности. То есть, базис — это те элементы, при помощи которых можно сделать любое устройство (речь идет о цифровой технике). Из указанных простейших базовых логических элементов собирают, конструируют сложные логические схемы ЭВМ. Например, сумматоры, шифраторы, дешифраторы и др. Большие интегральные схемы (БИС) и сверхбольшие (СБИС) интегральные схемы также содержат в своем составе (на кристалле кремния площадью в несколько квадратных сантиметров) десятки тысяч вентилей.
Это возможно еще и потому, что базовый набор логических схем (инвертор, конъюнктор, дизъюнктор) является функционально полным (любую логическую функцию можно представить через эти базовые вентили), представление логических констант в них одинаково (одинаковы электрические сигналы, представляющие 1 и 0) и различные схемы можно «соединять» и «вкладывать» друг в друга (осуществлять композицию и суперпозицию схем). На их основе можно сделать все вышеперечисленные элементы. Таким способом конструируются более сложные узлы ЭВМ — ячейки памяти, регистры, шифраторы, дешифраторы, а также сложнейшие интегральные схемы.
Кроме того, широкое распространение получили в реализации современных логических схем функции И-НЕ, ИЛИ-НЕ, исключающее ИЛИ.
«И-НЕ» — это схема И и схема НЕ, сложенные вместе. Операция, которую производит такой элемент, называется инверсией логического умножения или отрицанием логического умножения, или инверсией конъюнкции, а также штрих Шеффера. В виде формулы операция И-НЕ записывается так: F = X | Y.
Таблица истинности для этой функции представлена в следующем виде:
| X | Y | F |
Графическое изображение функции И-НЕ представлено на рис. 4.
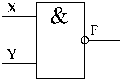
Рис. 4. Графическое представление функции И-НЕ
Операция, выполняемая элементом ИЛИ-НЕ, называется инверсией логического сложения или инверсией дизъюнкции и еще словосочетанием «стрелка Пирса». В виде формулы эта функция записывается так: F = X↓Y.
Значения этой функции при различных X и Y могут быть представлены в таблице истинности:
| X | Y | F |
На рис. 5 представлено графическое изображение инверсии логического сложения.

Рис. 5. Графическое изображение функции ИЛИ-НЕ
Операция, выполняемая таким элементом как «ИСКЛЮЧАЮЩЕЕ ИЛИ», обозначается плюсиком в кружочке, т. е. вот таким символом Å. В виде уравнения функция записывается так: F = XÅY. Читается это, как «либо икс, либо игрек». Таблица истинности элемента ИСКЛЮЧАЮЩЕЕ ИЛИ следующая:
| X | Y | F |
Элемент ИСКЛЮЧАЮЩЕЕ ИЛИ может быть представлен следующее схемой (рис. 6).

Рис. 6. Графическая реализация ИСКЛЮЧАЮЩЕГО ИЛИ
При преобразовании логических выражений следует учитывать приоритет выполнения логических операций. В порядке убывания старшинства, логические операции расположены в следующем порядке: отрицание, конъюнкция, дизъюнкция. Кроме того, на порядок выполнения операций влияют скобки, которые можно использовать в логических выражениях.
Табличный способ определения истинности сложного выражения имеет ограниченное значение, так как при увеличении количества логических переменных приходится перебирать слишком много вариантов. В таких случаях используют правила и законы алгебры логики, которые позволяют значительно упростить логические уравнения и функции.
Аналогично обычной алгебре, в булевой действительны свойства перестановки, сочетательности и распределительности:
a + b = b + a;
a ´ b = b ´ a;
a + (b + c) = (a + b) + c;
a ´ (b ´ c) = (a ´ b) ´ c;
a ´ (b + c) = a ´ b + a ´ c.
Помимо этих есть и другие, свойственные только алгебре логики, законы:
— Законы одинарных элементов:
a ´ 1 = a;
a + 1 = 1;
a ´ 0 = 0;
a + 0 = a;
— Законы отрицания (правила де Моргана):

— Распределительность дизъюнкции:
a + (b ´ c) = (a ´ b) + (a ´ c);
— Правила поглощения:
a + (a ´ b) = a;
a ´ (a + b) = a.
Таким образом, зная свойства цифровых устройств и основы булевой алгебры, недостающий элемент легко заменяется другими. Причем схемотехническая часть может быть любой, главное, чтобы выполнялось условие совпадения таблиц истинности. Подобным образом менять можно почти все, суть в том, чтобы максимально упростить схемотехнику при сохранении ее простоты и легкоповторяемости.
Упражнения
1.Чему равно количество различных комбинаций переменных для таблицы истинности логической функции а)F (a,b,c); б) F (k,l,m,n). Ответ представить в восьмеричной системе счисления.
2. Составить таблицы истинности для следующих логических функций:
а) ØXÚØYÚØZ;
б) XÙØYÙØZ;
в) ØXÙØYÙZ;
г) ØXÚYÚØZ.
ОТВЕТЫ К УПРАЖНЕНИЯМ
Двоичная система счисления
1. а) 1; б) 5; в) 8; г) 11; д) 15; е) 7; ж) 128; з) 16; и) 51; к) 100; л) 31; м) 255.
2. а) 10111; б) 100111; в) 110111; г) 110000.
3. 11001100.
4. 238.
