Восьмеричная система счисления

В восьмеричной системе счисления используются восемь цифр от 0 до 7. Подобно другим позиционным системам счисления, любое число в восьмеричной системе может быть представлено в виде соответствующего степенного ряда. Например:

327₈ = 3×8² + 2×8¹ + 7×8⁰ = 192 + 16 + 7 = 215₁₀;

111₈ = 1×8² + 1×8¹ + 1×8⁰ = 64 + 8 + 1 = 73₁₀.

В силу того, что основание восьмеричной системы соответствует целой степени числа 2 (8 = 2³), то перевод восьмеричных чисел в двоичную форму прост: для этого достаточно заменить каждую цифру этих чисел трехразрядным двоичным числом. При этом ненужные нули отбрасываются. Например,

	(2		3,	4)8	= (10111011,1)2;
	|	|	|	|

	(1		7,	6)8	= (1101111,110)2.
	|	|	|	|

При переводе из двоичной системы счисления в восьмеричную поступают следующим образом: влево и вправо от запятой разбивают двоичное число на группы по три разряда, дополняя при необходимости крайние группы нулями. Затем каждую группу из трех разрядов заменяют соответствующей восьмеричной цифрой. Приведем примеры:

			011,		= (11010011,111)2;
	|	|	|	|
	(3		3,	7)8

			011,		= (1010011,11)2.
	|	|	|	|
	(1		3,	6)8

Упражнения

1. Записать следующие восьмеричные числа в двоичном коде:

а) 3; б) 7; в) 0; г) 7642; д) 1036; е) 2105.

2. Записать следующие двоичные числа в восьмеричном коде:

а) 101; б) 110; в) 010; г) 111000101010; д) 1011000111; е) 100110100101.

3. Записать восьмеричное число в десятичном коде: 6724.

4. Записать десятичное число в восьмеричном коде: 2648.

ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ

В шестнадцатеричной системе счисления алфавит цифровых знаков состоит из 16 символов, причем в качестве первых десяти символов используются арабские цифры от 0 до 9, а дополнительно к ним применяются буквенные символы: 10 — А, 11 — В, 12 — С, 13 — D, 14 — Е, 15 — F. С помощью данного алфавита можно записать все десятичные числа от 0 до 15 включительно. Например:

D7₁₆ = D×16¹ + 7×16⁰ = 13×16 + 7×1 = 208 + 7 = 215₁₀;

49₁₆ = 4×16¹ + 9×1 = 64 + 9 = 73₁₀.

В силу того, что основание шестнадцатеричной системы соответствует целой степени числа 2 (16 = 2⁴), то перевод шестнадцатеричных чисел в двоичную форму также прост, как и для восьмеричной системы. Для перевода достаточно заменить каждую цифру шестнадцатеричных чисел четырехразрядным двоичным числом. При этом ненужные нули отбрасываются.

Например,

	(2	F	3,	4)16	= (1011110011,01)2;
	|	|	|	|

	(3	A	7,	E)16	= (1110100111,111)2.
	|	|	|	|

При переводе из двоичной системы счисления в шестнадцатеричную поступают аналогичным следующим образом: влево и вправо от запятой разбивают двоичное число на группы по четыре разряда, дополняя при необходимости крайние группы нулями. Затем каждую группу из четырех разрядов заменяют соответствующей шестнадцатеричной цифрой. Приведем примеры:

					= (101000110111,1011)2;
	|	|	|	|
	(A		7,	B)16

					= (111010100100,0011)2.
	|	|	|	|
	(E	A	4,	3)16

Упражнения

1. Записать следующие шестнадцатеричные числа в двоичной форме:

а) C; б) 6; в) F; г) E2; д) 1A; е) 3D; ж) AO; з) 8B; и) 45; к) D7.

2. Преобразовать следующие двоичные числа в шестнадцатеричный код:

а) 1001; б) 1100; в) 1101; г) 1111; д) 10000000; е) 01111110; ж) 0010101; з) 11011011.

3. Преобразовать следующие шестнадцатеричные числа в десятичный код:

а) 7E; б) DB; в) 12A3; г) 34CF.

4. Преобразовать следующие десятичные числа в шестнадцатеричный код:

а) 217; б) 48373.

ДВОИЧНО-ДЕСЯТИЧНЫЕ ЧИСЛА

С целью удобства преобразования чистые двоичные числа представляются десятичными либо шестнадцатеричными. Однако двоично-десятичное преобразование — операция не простая. В контрольно-измерительной аппаратуре, устройствах индикации, телефонах, калькуляторах, когда на доступных пользователю выходах и входах широко распространены десятичные числа, для их представления используют специальный двоично-десятичный код.

Микропроцессоры выполняют арифметические операции с двоичными числами, но также они обладают командами для преобразования результата в двоично-десятичный код. Полученные двоично-десятичные числа легко затем представить в десятичной записи, использую табличный метод перекодировки с использованием таблицы.

Упражнения

1. Записать следующие десятичные числа в двоично-десятичном коде:

а) 99; б) 82; в) 17; г) 40; д) 65; е) 39.

2. Записать следующие двоично-десятичные числа в десятичном коде:

а) 01010101; б) 01000011; в) 01110110; г) 10010010; д) 00000001; е) 10000000.

ДВОИЧНАЯ АРИФМЕТИКА

Достоинством двоичной системы счисления, используемой в ЭВМ, является простота выполнения арифметических операций. Арифметические действия с двоичными числами выполняются по следующим правилам:

сложение	вычитание	умножение
0 + 0 = 0	0 – 0 = 0	0 ´ 0 = 0
0 + 1 = 1	1 – 0 = 1	0 ´ 1 = 0
1 + 0 = 1	1 – 1 = 0	1 ´ 0 = 0
1 + 1 = 0 + 1 переноса в старший разряд	10 – 1 = 1	1 ´ 1 = 1

В случае многоразрядных двоичных чисел арифметические операции выполняются подобно тому, как это делается в десятичной системе счисления. Например, при сложении необходимо учитывать возможные переносы единицы из младших разрядов в старшие. При вычитании многоразрядных двоичных чисел может оказаться необходимым «занять» единицу в старшем разряде, что дает две единицы в младшем разряде. Умножение двоичных чисел сводится к умножению множимого на каждый разряд множителя, и последующему сдвигу множимого или множителя и суммированию образующихся частичных произведений. Деление двоичных чисел производится путем последовательного выполнения вычитаний и сдвигов. Например:

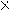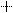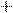Упражнения

1. Выполнить следующие сложения двоичных чисел:

а) 1010 + 0101; б) 1101 + 0101;

в) 01011011 + 00001111; г) 00111111 + 00011111.

2. Выполнить следующие вычитания двоичных чисел:

а) 1110 – 1000; б) 1010 – 0101;

в) 01100110 – 00011010; г) 01111000 – 00111111.

3. Выполнить следующие умножения двоичных чисел:

а) 1001 ´ 11; б) 1101 ´ 1001; в) 1111 ´ 101; г) 1110 ´ 1110.