Парадокс 3: хвастливый цирюльник

Луиджи, цирюльник из Севильи, горделиво хвастался своими успехами.

«Ты знаешь, я — тот человек, который бреет всех и только тех жителей Севильи, которые не бреются сами!»

«Я тебе не верю», — отвечал Франко.

«Почему же?»

«Вот почему. Ты сам-то бреешься? Если бреешься, то из того, что ты сказал, следует, что ты себя не бреешь. Ты же сказал, что бреешь всех и только тех жителей, которые не бреются сами. Верно?»

«Верно, верно. Но что, если я скажу, что сам не бреюсь — это делает за меня моя жена?»

«Но если ты сам не бреешься, значит, сам себя бреешь. Ты же сказал, что бреешь всех, кто не бреется сам. Так ведь?»

«Да, пожалуй, что так».

Так бреет Луиджи тех, кто сам не бреется, или нет?

Парадокс 4: Ахиллес и черепаха

Ахиллес мчится на мощном мотоцикле. Черепаха едет на маленьком мопеде. Они решили устроить соревнование. Но поскольку мотоцикл Ахиллеса гораздо быстрее мопеда черепахи, Ахиллес дает ей фору — она начинает движение, будучи на некотором расстоянии впереди него.

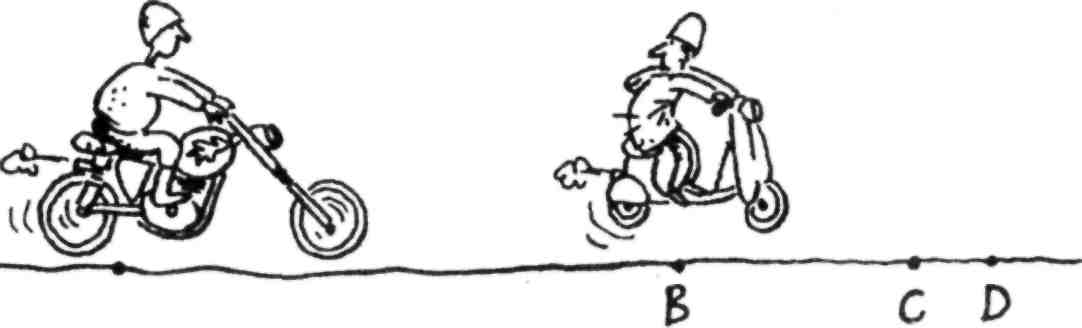
А

Ахиллес стартует в точке А. Черепаха стартует в точке В. Пока Ахиллес доедет до точки В, черепаха продвинется до точки С. Когда Ахиллес достигнет точки С, черепаха доедет до точки Д. Всякий раз, когда Ахиллес достигает той точки, где была черепаха, она успевает переместиться в другую, более далекую точку. Таким образом, Ахиллесу нужно преодо-

леть бесконечное число промежутков, отделяющих его от черепахи. Но преодолеть бесконечного количества отрезков он не может, в этой последовательности нет последнего отрезка. Поэтому Ахиллес никогда не догонит черепаху. Конечно, он ее догонит. Но как?

Парадокс 5: вороны

Плак расспрашивает представителя науки Бриди о том, чем занимаются ученые.

Плак: Как действует наука?

Бриди: Ну, ученые создают теории, которые затем подтверждают наблюдениями.

Плак: Приведи мне какой-нибудь пример.

Бриди: Хорошо. Возьмем общее утверждение о том, что все вороны черные. Все обобщения подтверждаются их конкретными частными случаями. Так, например, наблюдение какого-то черного ворона, будучи частным случаем общего утверждения о том, что вороны черные, подтверждает это общее утверждение. Каждый черный ворон подтверждает в какой-то степени гипотезу о том, что все вороны являются черными.

Плак: Понимаю, понимаю. Но скажи, верно ли, что если две гипотезы логически эквивалентны, то все, что подтверждает одну гипотезу, должно подтверждать также и другую гипотезу?

Бриди: Это должно быть верно. Логически эквивалентные гипотезы фактически представляют собой лишь два разных способа сказать одно и то же. Поэтому все, что подтверждает одну такую гипотезу, должно подтверждать и другую.

Плак: Совершенно верно. Но гипотеза «Все вороны черные» логически эквивалентна гипотезе «Все не-черные предметы являются не-во-ронами».

Бриди: Конечно. По сути дела, они говорят одно и то же.

Плак: В таком случае если все обобщения подтверждаются своими примерами, то не-черные не-вороны подтверждают утверждение о том, что все не-черные предметы являются не-воронами, верно?

Бриди: Плак:

Бриди: Плак:

Бриди: Плак:

Верно.

Но тогда не-черные не-вороны подтверждают, что все вороны черные, так? Пожалуй, так.

Поэтому и белые ботинки, и красные маки, и голубые небеса, будучи не-черными не-воронами, подтверждают гипотезу «Все вороны черные».

Но это же абсурд!

Однако это вытекает из того, с чем ты согласилась раньше. Даже вот эта башня из розового мороженого подтверждает, что все вороны черные!

Плак прав: если согласиться с тем, что сказала Бриди, то даже порция розового мороженого подтверждает, что все вороны черные. Но ведь это же абсурд! Или нет?

Парадокс 6:
неожиданная
проверка

Учитель говорит своим ученикам, что на следующей неделе

их ожидает проверка. Однако он не сообщает им, в какой день будет проведена эта проверка. Проверка должна быть для них неожиданной.

Но будет ли она неожиданной?

Можно ли провести проверку в пятницу? Нет, нельзя. Если учитель захочет провести ее в пятницу, то, зная о том, что это последний день учебной недели, ученики будут ожидать ее именно в этот день. В пятницу проверка не будет неожиданной.

Ну а как насчет четверга? Ученики знают, что в пятницу проверка состояться не может. Поэтому если ее не было в предшествующие дни, ученики будут ожидать ее в четверг. В четверг проверка также не будет неожиданной.

А что со средой? Опять-таки и среда отпадает. Ученики знают, что в пятницу и в четверг проверки быть не может. Если учитель отложил ее на среду, то в среду ученики будут ожидать ее. Она не будет для них неожиданной.

По тем же причинам устраняются вторник и понедельник.

Короче говоря, учитель не может провести неожиданную проверку.

Или все-таки может?