Глава 10. Последовательность правителя Вэня как числовое выражение модульной иерархии

Глава 9 вводит понятие простой волны, извлечённой нами из последовательности правителя Вэня особым графопостроением. Глава 9, по сути, обосновывает возможность использования простой волны в качестве первичной единицы модульной иерархии – были продемонстрированы организующие принципы последовательности правителя Вэня. Эта простая волна переходов в прямом и обратном порядке, в единичной полной последовательности И цзина правителя Вэня (рис. 18 Б), может легко быть моделью физической структуры расщеплённой ДНК и её трансформаций: репликации, дупликации, транскрипции. Это – «микропипеточные» функции ДНК, которые ничего не говорят о гармоничных динамических отношениях в живом мире клеточного ядра. Биологи ещё даже не взялись за системные свойства живой клетки, хотя хорошо изучили функции одноцепочечной ДНК.

Если интеркаляция 5HT считается частью метаболизма 5НТ (см. рис. 9) и она происходит постоянно в участках вставки между кодонами, тогда картина ЭПР в ДНК должна существенно меняться. Представляется возможным, что интерферограммы, генерируемые сдвигом ЭПР-сигнатур, лежат в основе механизма голографической стоячей волны, используемого живой системой для моделирования внешнего мира внутри себя. Лишь 10% ДНК направлено на синтез белка. Оставшиеся 90% в молекуле представляют загадку. На наш взгляд, организм выстраивает и поддерживает внутренний горизонт опыта в энергетическом континууме на основе и под управлением ДНК нейронов. Мышление и рефлексия могут быть голографическими функциями, проявляющимися на фоне энергетического потока подконтрольного ДНК метаболизма. В сущности, ощущаемый организмом поток биохимической энергии и есть само время. Жизнь эволюционировала в виды, отвечая этому потоку.

Мы надеялись применить идею модульной иерархии к простой волне, используя варианты резонансных циклов из наших календарных исследований. Так мы хотели картировать континуум временны́х переменных. Если теория верна, полученные карты будут представлять собой графики континуума метаболической энергии, которую мы все называем временем. Эти графики релевантны для каждого, поскольку его или её жизнь есть проявление ДНК в онтогенезе. Эти графики релевантны и в отношении истории, которая есть не что иное, как время вида Homo Sapiens: она проявление ДНК в филогенезе. Для картирования континуума временных переменных мы выбрали простую волну (рис. 18 Б), которая сама по себе является сложным выражением всего И цзина. Эту волну мы положили первичной единицей иерархии, в которой каждый уровень структурирован на тех же принципах, что вышестоящие и нижележащие. Определение модульной иерархии:

Центральной идеей модульной иерархии является модуль. Это структура или система, могущая рассматриваться и как целое, и как часть. Как целое, модуль разложи́м на субмодули нижележащего уровня. Как часть – стыкуем в сверхмодули вышерасположенного уровня.

… термин модуль, используемый здесь в общем смысле, не требует точной формулировки. Но мы можем ассоциировать его с двумя фундаментальными свойствами:

1) модуль обладает некоторой замкнутостью или частичным замыканием (Уилсон 1969). Эта замкнутость может быть топологической, временнóй или определяться неким операциональным правилом, как в теории групп

2) модуль обладает некоторой степенью полуавтономии в отношении других модулей и их ситуации

Эти два свойства представляются общими во всех модульных иерархиях

(Альберт Уилсон в сборнике под ред. Ланселота Ло Уайта и Донны Уилсон, 1969, стр. 115)

Вспомните из главы 8, что первичная единица в И цзине – это линия, или яо. Полная последовательность шестидесяти четырёх гексаграмм содержит 384 яо. Иерархический надуровень для яо – гексаграмма, состоящая из шести яо. Традиционно гексаграмма разбивается на две половинки по три линии. Эти половинки называются триграммы; две триграммы формируют гексаграмму. Следуя этому же принципу, мы выстроили шесть простых графиков в цепочку. Они аналогичны шести линиям гексаграммы. На них мы наложили – так же гуськом – ещё две простые волны: каждая втрое больше любой из первых шести малых волн. Эти волны побольше – эквиваленты двух триграмм гексаграммы. Поверх последовательности из шести и двух – финáльная простая волна, обозначающая всю гексаграмму. Это однократная волна. Она вшестеро больше любой из шести волн первичного уровня и вдвое больше любой из двух волн промежуточного уровня (рис. 19). Генерируемая таким образом трёхуровневая структура является детализацией простого графика рисунка 18 Б. Она полный аналог гексаграммы. Когда эта модульная иерархия – сложная волна – расширяется дальше, она становится аналогичной единичной гексаграмме И цзина: как часть ещё большей иерархии на правах одной шестьдесят четвёртой от целого. Каждый трёхуровневый модуль или сложная волна является 1/64 ещё большего модуля. Полученная сверхсложная волна имеет на первейшем уровне 384 элемента или 6 · 64 единицы: так же, как вся последовательность И цзина состоит из шестидесяти четырёх гексаграмм по шесть линий каждая, т.е. из 384 яо. Мы знаем, что 384 дня – это почти точная продолжительность тринадцати лунных циклов. Будем исходить из этого, а также из идеи, что органические макромолекулы структурируются ответно периодичности того или иного астрофизического фактора – в особенности, гравитации. Наша гипотеза заключается в том, что лунные циклы оказали формирующее влияние на структуру ДНК. Мы также полагаем, что 384-дневный цикл лунных влияний – это важнейший природный календарь, касающийся любого эволюционировавшего на Земле вида. Этот 384-дневный цикл есть первичный цикл большой биологической значимости. В качестве подуровня он входит в глобальную иерархию в 64 раза длиннее себя. Мы назвали его лунным годом. На наш взгляд, это всего лишь один из уровней многоуровневой иерархии. Каждый уровень описывается волной рисунка 19.

Для описания всей тотальности существования во времени необходима 26- уровневая иерархия. Можно исходить из универсальности рисунка 19 применительно к любому из двадцати шести уровней. Когда рисунок 19 берётся как 384-дневный лунный календарь, каждому дню соответствуют 3 пары (встречных) гексаграмм – по паре с каждого из трёх уровней 6:2:1. Влияние меньших циклов на каждом из уровней (см. таблицу III рис. 20) добавляет опыту бытия колорит, тональность и чувство: именно эти меньшие шкалы и интерфазы между ними ответственны за тончайшие детали, придающие жизни глубину и неоднозначность. Эти эпициклы и интерфазы обрекают на неудачу детерминистский подход к точным пространственно- временным координатам событий. Общие расчёты – основанные на бóльших временны́х шкалах – лежат в основе эмпирического базиса нашего собственно исследования в этом направлении: касательно иерархии И цзина и её отношения к времени.

Лунный год представляет собой процесс во времени, формирующий гексаграмму – полный энергетический гештальт – в пространстве-времени. Эта форма требует 6 x 64 дня для завершения, поскольку шестичастна: из шести линий или яо. Каждой такой части требуется 64 дня для завершения. Лунный год, в свою очередь, является 1/64 большего цикла. Тот – 1/64 ещё большего цикла (см. таблицу I рисунка 16). Сам лунный год состоит из шестидесяти четырёх шестидневок, каждая из которых описывается всё той же сложной волной, моделирующей их. Это гексаграммы шестидневной длительности. Каждая шестидневка, в свою очередь, это целое, состоящее из ещё 64 частей. Каждая такая часть – точная копия целого. И так далее в сторону уменьшения: всё более короткие 64-частные циклы – до планковских величин. Дальнейшее дробление времени не имеет смысла в физике, поэтому на уровне ħ фрактальность прекращается. Итак, модульная иерархия начинается с планковских величин. На наш взгляд, различные временны́е уровни – это обертонные гармоники квантовомеханического потока циклических атомарных временны́х переменных. Если принять идею, что вселенной присуща такая временнáя иерархия, это приводит к проблеме природы и необходимости финального времени, в рамках такой теории.

Таблица III

Уровни и длительности временнóй иерархии*

1)	2,280 · 1018 секунд	(72,25 миллиардов лет)	делим на 64
2)	3,562 · 1016 секунд	(1,129 миллиарда лет)	»	»
3)	5,566 · 1014 секунд	(17 миллионов 638 тыс. лет)	»	»
4)	8,697 · 1012 секунд	(275 тысяч 600 лет)	»	»
5)	1,359 · 1011 секунд	(4306 лет 97,5 дней)	»	»
6)	2,123 · 109 секунд	(67 лет 104 дня 6 часов)	»	»
7)	3,318 · 107 секунд	(384 дня – 13 лунных месяцев)	»	»
8)	5,184 · 105 секунд	(6 дней)	»	»
9)	8,100 · 103 секунд	(135 минут)	»	»
10)	1,266 · 102 секунд	(127 секунд)	»	»
11)	1,978 · 100 секунды	(1,98 секунды – инфразвук)	»	»
12)	3,090 · 10–2 секунды	(5-я гармоника Шумана)	»	»
13)	4,828 · 10–4 секунды	(ЗЧ ≃ до4)	»	»
14)	7,544 · 10–6 секунды	(НЧ)	»	»
15)	1,179 · 10–7 секунды	(ВЧ)	»	»
16)	1,842 · 10–9 секунды	(УВЧ)	»	»
17)	2,877 · 10–11 секунды	(КВЧ)	»	»
18)	4,496 · 10–13 секунды	(терагерцевое излучение)	»	»
19)	7,026 · 10–15 секунды	(ИК)	»	»
20)	1,098 · 10–16 секунды	(экстремальный УФ)	»	»
21)	1,715 · 10–18 секунды	(рентген)	»	»
22)	2,680 · 10–20 секунды	(мягкое гамма-излучение)	»	»
23)	4,188 · 10–22 секунды	(жёсткое гамма-излучение)	»	»
24)	6,543 · 10–24 секунды	(жёсткое гамма-излучение)	»	»
25)	1,022 · 10–25 секунды	(жёсткое гамма-излучение)	»	»
26)	1,597 · 10–27 секунды	(гамма-излучение сверхвысоких энергий)

* значения в секундах вычислены с большой мантиссой, но округлены до

третьего знака

РИСУНОК 20

Таблица III демонстрирует модульную иерархию временны́х интервалов на двадцати шести уровнях, дающих всю полноту охвата существования во времени. В основе соседствующих уровней – всё та же сложная волна рис. 19

Конечный результат вложенного самоподобия временнóго континуума на уровнях иерархии большой длительности может быть связан с видимой конденсацией голограммы ума в виде лучезарного образа, стоячей волны. Организмы вовлечены в нескончаемый процесс совершенствования своего познания мира. Окончательно уяснить себе природу этого феномена не представляется возможным. Сколь бы ни была точна та или иная формулировка, она сильно зависит от своих граничных условий. Во втором веке н.э. александрийские мыслители – в особенности, Климент – углубились в Откровение Иоанна. В Апокалипсисе их, прежде всего, интересовала природа тела воскрешения. Вопрос даты второго пришествия Сына Человеческого казался менее важным:

В тот великий день люди воссоединятся со своими телами – гласит Писание. И именно этот момент вызывал наибольшее смущение современников: христиане были совершенно озадачены, полемизирующие с ними язычники имели лишний повод для презрения и насмешек. Ориген, как и Климент, разрешил все свои сомнения, обратившись к посланиям св. Павла. В них он заново прояснил для себя этот момент: воскрешённое тело будет таким же, какое у нас сейчас – но и отличаться будет тоже. Оно будет другим, поскольку:

· материальное тело станет одухотворённым и сияющим

· это будет другая материя

В то же время, это будет всё то же тело: мы сейчас – это мы два десятилетия назад: атомы сменились, но идентичность та же. Душа – ассимилирующая искра жизни – содержит в себе некий принцип подгонки близлежащей материи. Душа лепит из неё удобное для себя пристанище. Та же сила, которую душа использует еженощно для восстановления дневного износа организма, посмертно направляется на восстановление окончательного износа: душа сооружает себе новую обитель. Монахи-оригенисты считали, что тело воскрешения круглое. Впоследствии Юстиниан Великий осудил это убеждение и предал Оригена анафеме (Бигг 1913, стр. 271-272)

Теория общего доступа к генетической памяти, отражения её контента в ДНК на квантово-биохимическом уровне – вполне удовлетворительно объясняет появление у шаманов стойкого предчувствия. Можно говорить о наличии такого предчувствия у человечества в целом: предчувствия загробной жизни и коллективной трансформации. Она неизбежна. И она порождает ударную волну хаоса сейчас, в конце времён. Выйти на точную дату этой колоссальной «ломки льдов» непросто. Большинство милленариев трактуют Откровение 20:4 в пользу ближайших к себе лет.

В предлагаемой нами модульной иерархии пространства-времени полная энергия континуума полностью содержится и в каждом резонансном подуровне.

[ср. упанишады («Ишавасья»)

– прим. пер.]

Эта идея неизбежно следует из организменной мысли: каждый модуль иерархического континуума вмещает в себя весь континуум. Складка временны́х ограничений – особенно определяющая темпоральный нексус в пространстве – это место, где типичные для высших пространственных измерений виды связей вторгаются в мир обычного пространства-времени. И это место, в каком-то смысле, везде: потенциально это любая точка. Модули суть базовые единицы квантованной или дискретно выраженной иерархической структуры, каждый уровень которой наследует форму первичного уровня. Представляет интерес момент обратной эвольвенты временнóй иерархии в свои короткие эпохи. Будучи людьми современными и по натуре скептиками, мы посчитали маловероятным, что такое случится прямо сейчас. Хотя гипотеза и указывает на возможность ингрессии сращения (временнóго многообразия).

Мы полагаем, что пространство-время – это поток новизны. И переменные этого потока предсказуемы. Исходя из этого предположения, мы попытаемся найти числовое выражение скачков временных параметров. Это даст возможность спрогнозировать ход вторжений новизны в пространство-время (см. Приложение). Это, в принципе, не сложная задача. Всё что требуется – это логически последовательная техника индексирования каждой точки модульной иерархии дискретным значением. Эмпирическое исследование гипотезы потока временны́х параметров не продвинется дальше, пока не будут найдены значения квантификации. Числовое выражение каждой точки в иерархии – с идеальным и окончательным состоянием, квантифицированным как ноль – даёт относительную шкалу значений. Мы использовали эти относительные значения для картографирования интенсивности вторжения новизны в историю. Нашей задачей было увидеть, действительно ли полученная схема предсказывает вторжения новизны в реальный пространственно-временной мир. Избавиться от сомнений в смысле временнóй волны возможно только через квантификацию. Иначе волна и её интерпретация, в лучшем случае, просто мистическая доктрина. После ряда шагов, логически безукоризненных и интуитивно верных, нам удалось численно выразить волну. Форсировать проблему мы начали с рассмотрения простой волны рисунка 18 Б.

Было обнаружено: простой график задают 13 типов линий, независимо от масштаба. [В самом графике линий 11 – прим. пер.] Тринадцать векторов показаны на рисунке 21. Поскольку эти длины всегда дискретные элементы, можно придать им целочисленные индексы в порядке возрастания.

Простая волна – сетка делает возможным вычисление колен графика

[6 скаляров межгексаграммных переходов: 1, , 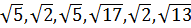– прим. пер.]

РИСУНОК 21

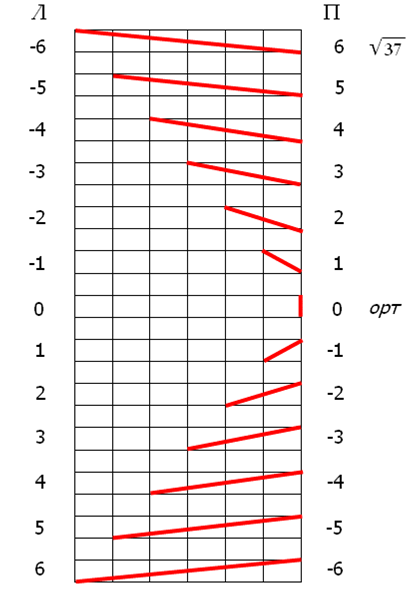
Тринадцать векторов задают простую волну рисунка 18 Б. Для учёта компланарных тангенсов вместе с антипараллельностью, прямонаправленные вектора получили отрицательные индексы, а противоположно направленные – положительные. Значения колонки «Л» предназначены для левой стороны простой волны, колонки «П» – для правой; это те же значения, но их знак противоположный. Числа на рисунке 21 позволяют квантифицировать длины векторов.

Числа больше нуля означают падающую линию, меньше нуля – растущую. Модуль числа в сочетании со знаком адекватно отражает модуль и аверс-реверс вектора. Числа слева относятся к прямому графику, числа справа – к обратному: к правому краю простой волны. Это те же самые числа, но со знаком минус. Знак нужен только при суммировании значений шкалы и при итоговом графическом построении объединённых значений не принимается во внимание – любой из двух наборов значений может применяться как справа, так и слева, но проходиться должен сначала и до конца. На рисунке 22 изображена простая волна с индексами рисунка 21.

Важно иметь в виду, что значения на рисунке 22 сделаны для простой волны мельчайшего масштаба в составе сложной волны. Относительные пропорции трёх уровней сложной волны сохранены и снабжены числовым аналогом, который есть соответствующий индекс исходной шкалы, взятый с нужным коэффициентом. Так, для срединной (триграммной) шкалы исходное значение рисунка 22 умножалось на тройку, так как триграммная шкала втрое больше исходной (линейной). Точно так же, гексаграммные позиции получили числовые аналоги с коэффициентом 6 против исходного индекса. Это потому, что шкала гексаграммы вшестеро больше линейной. Рисунок 22 основан на индексах рисунка 21 и является именно тем вариантом распределения значений, который мы использовали во всех наших вычислениях.

Отметим, что на рисунке 22 все параллельные линии, независимо от расстояний между ними, сокращены до нуля: указанная последовательность действий позволяют численно выразить направление наклона, масштаб и уклон – но не колеблющееся расстояние между границами волны. Необходимые показатели можно найти схожим образом, но процедура несколько иная.

Рисунок 23 показывает 7 типов дивергенции (расхождения), конгруэнции (схождения) и нахлёста, которые демонстрируют точки простой волны. Справа и слева на рисунке – возрастающая и убывающая нумерации, маркирующие возрастание или убывание волны в данном участке. Мы решили использовать правосторонний подход [ср. правосторонний базис в векторном исчислении – прим. пер.] для сохранения интуитивного ощущения, что нахлёст ведёт ситуацию к нулевой точке, а не вспять. Рисунок 24 демонстрирует значения, генерируемые индексами точек в отношении простой волны. На рисунке 25 объединены значения правого и левого уклона, параллельности и относительных размеров – по вышеназванной схеме. 384 позиции с их соответствующими значениями являются квантификацией трёхуровневой волны рисунка 19. Эти же значения вычерчены как однолинейный график рисунка 26. Рисунок 25, банк значений рисунка 26, лежит в основе индексации любой сложной волны, а процесс поиска значений на каждом последующем уровне в её модульной иерархии обязательно исходит из данных рис. 25.

На рисунке 26 вычерчены составные значения отдельной сложной волны. Эти значения показаны на рисунке 25. Рисунок 26 расслаивает комплексную, трёхуровневую, двусторонне текущую сложную волну рисунка 19 в линию с односторонним движением. Рисунок 26 сохранил некоторые качества сложной волны (рис. 19), а именно:

· отход от нулевого состояния, где линии параллельны

· аверс-реверс-градус сдвоенных линий

· относительные пропорции всех трёх уровней

· расстояния между пульсирующими границами составляющих волн

Рис. 26 не отражает сдвига значений, который произойдёт, если однолинейную сложную волну вставить в ту или иную позицию в модульной иерархии сложных волн с наследуемыми 64-кратными уровнями.

РИСУНОК 22

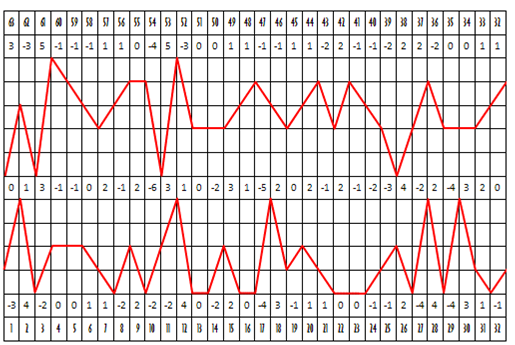
Значения рисунка 21 использованы для квантификации степени и направления наклона простой волны рисунка 18 Б. Обрамляющий крайний верхний и нижний ряд цифр представляют собой номера гексаграмм. Соседние с ними внутренние ряды цифр – это значения квантификации. [Центральный ряд цифр представляет собой алгебраическую сумму соответствующих пар квантификации верхнего и нижнего графиков; значения квантификации легко просчитываются по количеству клеточек сетки – прим. пер.]

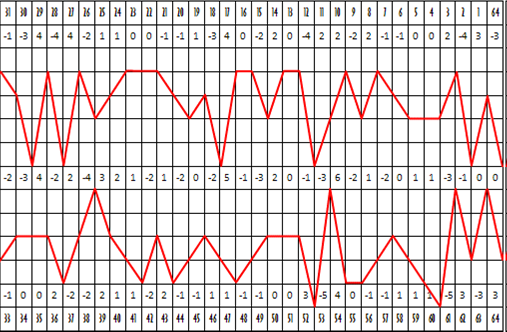
РИСУНОК 23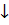

Семь типов разбегания (1), схождения (5) и нахлёста (1), демонстрируемые

вершинами простой волны рисунка 18 Б

Смыкание верхнего и нижнего графиков позволяет видеть 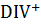и ,

отражённые далее в центральном ряде чисел рисунка 24:

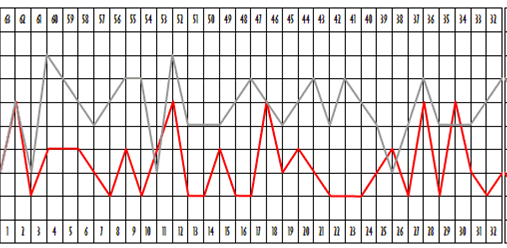
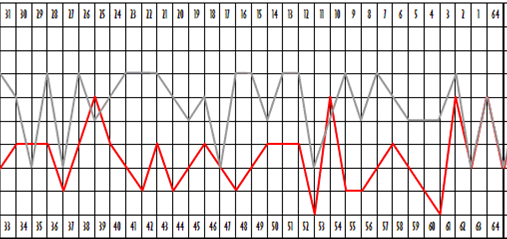
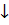РИСУНОК 24

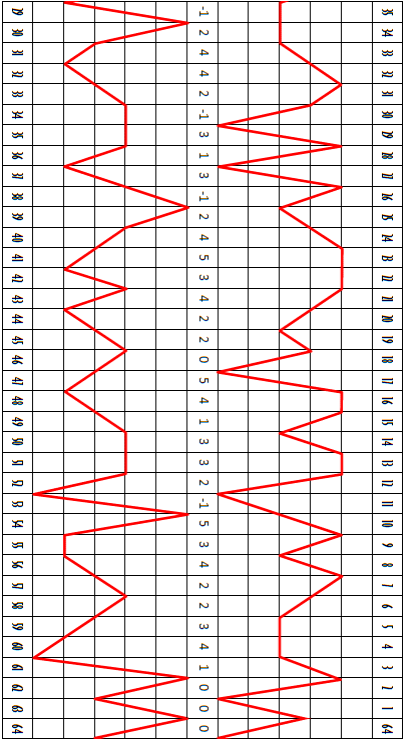
Значения центрального пояса получены применением левого ряда чисел рисунка 23 к простой волне рисунка 18 Б. Обрамляющие возрастающий и убывающий ряды цифр – это гексаграммы. Центральный ряд – квантификация положительной и отрицательной дивергенций.

[Подробно данные графики можно видеть в исполнении автора на сайте http://www.levity.com/eschaton/Watkinsanswered.html – прим. пер.]

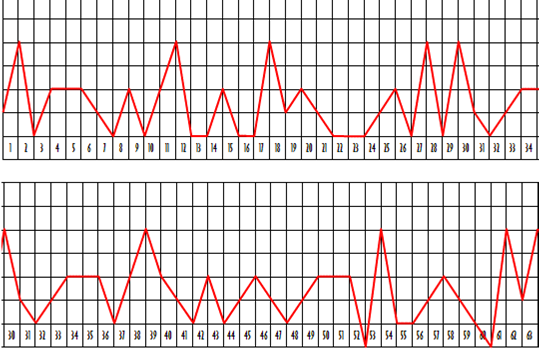
Таким образом, рисунок 26 представляет собой таблицу комбинированных значений, полученных наложением со значениями любого из 64 сегментов следующего большого уровня. Комбинированные значения получены умножением на 64, что означает их переход в последующий большой уровень иерархии. Отсюда берутся 64 варианта рисунка 26. Эти волны мы использовали как временны́е карты для любого интервала истории. Математика наследования одного уровня иерархии другим реализована в компьютерной программе «Временнáя волна ноль» для DOS и Java. Питеру Майеру удалось выразить теорию математически – в Приложении «Математика временнóй волны ноль» в конце книги. Квантификации каждой из 384 позиций рисунка 19 выведены на рисунке 25. Значения таблицы 25 положены в основу дискретных карт временнóго потока – из чего, собственно, и выводится идея фрактальной иерархической структуры времени. Обратите внимание, что таблица 25 выстраивает значения в обратном порядке в сравнении с рисунком 26. Последние три из 384 сегментов волны на любом уровне содержат особые точки (сингулярности), выраженные нулями: рисунок 26, нижний правый угол. Когда волна на любом из уровней входит в такие свои сегменты, являющиеся нулевыми состояниями, она снимает ограничения с нижерасположенных подуровней. Снятие ограничений вышестоящим уровнем в иерархии приводит к числовому провалу, стремящемуся к нулю. Это происходит всякий раз, когда на каком-то иерархическом уровне подходит к завершению цикл. Такие скачкообразные переходы от одной модальности к другой Уайтхед называет сменой эпох. Появление жизни в неорганическом мире, сознания в бессознательном мире, языка в мире без такового – это всё примеры таких эпохальных переходов. Жизнь каждого человека наполнена такими переходами, но они заканчивают лишь относительно короткие циклы в квантифицированной иерархии. Когда же заканчиваются циклы или эпохи действительно большой длительности, это приводит к крайнему ускорению в направлении нуля. Этот момент схож с Уайтхедовской концепцией сращения, как и с учением Махабхараты о сокращающихся югах. Спиральный образ в Апокалипсисе – ещё один пример интуиции, что время – это серия сжимающихся циклов с последующей скачкообразной трансформацией (Норман Кон, 1970).

На рисунке 26 объединены четыре момента: 1)дивергенция от нулевого состояния (когда линии параллельны), 2)направленность и степень уклона пар линий, 3)расстояния между сегментами волны, 4)пропорции всех трёх составляющих относительно последующих уровней – в единой волне.

Сводная таблица квантификации направленности-уклона и схождения- расхождения (гексаграммы 1-32)

№ гексаграммы	направленность-уклон	схождение-расхождение
	-1
	-1
	-1
	-6	-1
	-2
	-5
	-1
	-1
	-2
	-3	-1
	-2
	-4	-1

Сводная таблица квантификации направленности-уклона и схождения- расхождения (гексаграммы 33-64)

№ гексаграммы	направленность-уклон	схождение-расхождение
	-2
	-3	-1
	-2
	-4	-1
	-2
	-2
	-2
	-1
	-3
	-1
	-3	-1
	-2
	-2
	-3
	-1

То же, со сдвигом дивергентного ряда на позицию вниз и суммированием модулей:

гексаграммы	направленность-уклон	схождение-расхождение	lal + lbl
1-64
2-1
3-2
4-3	-1
5-4	-1
6-5
7-6
8-7	-1
9-8
10-9	-6
11-10		-1
12-11
13-12
14-13	-2
15-14
16-15
17-16	-5
18-17
19-18
20-19
21-20	-1
22-21
23-22	-1
24-23	-2
25-24	-3
26-25		-1
27-26	-2
28-27
29-28	-4
30-29		-1
31-30
32-31

гексаграммы	направленность-уклон	схождение-расхождение	lal + lbl
33-32	-2
34-33	-3
35-34		-1
36-35	-2
37-36
38-37	-4
39-38		-1
40-39
41-40
42-41	-2
43-42
44-43	-2
45-44
46-45	-2
47-46
48-47	-1
49-48	-3
50-49
51-50
52-51	-1
53-52	-3
54-53		-1
55-54	-2
56-55
57-56	-2
58-57
59-58
60-59
61-60	-3
62-61	-1
63-62
64-63

Выделенные жирным 0 (первая строка) и 0, 0, 2, 7, 4, 3, 2, 6 (последние восемь строк снизу вверх) представляют собой последнюю девятку трёхсот восьмидесяти четырёх опорных чисел набора Келли – Уоткинса / Майера (см. рис. 25)

Запишем вышеуказанную таблицу следующим образом, меняя знак направленности-уклона на противоположный:

позиция	направленность-уклон	схождение-расхождение
	-1
	-3
	-2
	-2
	-3	-1
	-1
	-3
	-1
	-2
	-2
	-2
	-4	-1
	-2
	-3	-1
	-2
	-4	-1
	-2
	-3	-1
	-2
	-1
	-1

позиция	направленность-уклон	схождение-расхождение
	-5
	-2
	-6	-1
	-1
	-1
	-1

Продублируем колонку направленности-уклона трижды, таки́м образом: утроенное значение с шагом в утроенную позицию, ушестерённое значение с шагом в шесть позиций подряд. Мы получили индексы для триграммной и гексаграммной части графика. Подобная процедура утроения / ушестерения – при соответствующем занятии трёх / шести позиций на месте прежней одной – повторяется для колонки схождения-расхождения (рекомендован Excel):

ПОЗИЦИЯ	направленность-уклон	схождение-расхождение	n
Л	Т	Г		—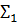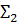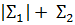
	-1	-3	-6	-10
	-3	-3	-6	-12
		-3	-6	-8
		-9	-6	-14
		-9	-6	-15
	-2	-9	-6	-17
			-18	-14
	-2		-18	-17
			-18	-9

в случае если 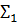< 0. , берется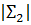

Таблица продолжается до позиции 384. Шестьдесят четыре значения первой (линейной) колонки повторяются шесть раз подряд, значения триграммной колонки повторяются два раза. Последняя колонка (модуль суммы трёх уровней направленности-уклона плюс сумма (модуль суммы) трёх уровней схождения-расхождения) и даёт то, что известно как опорные числа Ройса Келли (вывел их с помощью миниЭВМ в 1974) / Мэтью Уоткинса (нашёл в процедуре «мистическое» полуобращение: изменение знака части данных нач. с поз. 32) / Питера Майера (исправил «мистический» полуповорот):

10 13 12 20 20 22 36 38 32 32 33 33 41 34 39 40 32 32 39 44 40 33 33 32 40 50

44 17 20 22 37 39 38 28 38 32 44 47 49 33 37 32 5147 49 41 40 37 6363 62 71

77 75 26 3026 22 23 28 3533 33 30 31 34 41 40 38 33 38 34 26 17 18 48 50 43

38 33 35 23 25 24 41 40 38 41 45 43 71 79 68 66 70 68 32 22 32 04 04 0727 30

34 25 23 23 49 40 51 19 11 15 44 41 47 48 49 47 53 52 5343 38 36 42 42 4340

47 46 38 36 41 52 62 47 43 45 47 31 36 43 23 19 2130 32 31 42 41 31 32 26 34

05 09 13 45 44 34 55 57 53 50 52 53 25 20 24 17 19 10 3637 29 48 49 5029 37

32 30 26 27 38 43 38 36 36 36 34 37 36 44 44 46 38 34 4426 31 33 37 40 41 42

44 44 33 38 34 27 27 26 42 40 42 47 50 52 19 17 1424 22 24 38 41 43 23 21 22

41 41 39 65 64 61 47 51 5253 41 55 28 30 26 42 43 40 53 51 51 48 4952 35 34

32 27 32 28 32 35 36 30 28 31 30 37 25 53 51 56 47 46 44 47 51 49 57 53 56 64

64 66 14 18 16 30 26 29 33 36 40 31 29 29 49 40 51 19 21 21 34 35 23 46 41 45

41 42 43 43 42 42 60 60 61 52 51 5026 28 29 40 50 35 5757 55 61 62 57 1923

2126 26 27 30 29 21 22 24 22 35 3943 39 38 36 53 47 55 56 60 63 25 20 24 17

19 14 16 13 15 24 25 26 5 13 8 6 2 3 4 7 2 0 0 0 РИСУНОК 25

&nb