Метод минимизации с помощью карт Вейча.
Алгоритм метода карт Вейча включает в себя следующие этапы:
1. Любая формула приводится к СДНФ.
2. Составляется карта Вейча. Карта Вейча – это таблица всех возможных комбинаций значений переменных. В соответствующие ячейки заносятся единицы, соответствующие конституентам СДНФ.
3. Единицы, стоящие по вертикали и горизонтали, объединяются (по 2 , по 4 . по 8 и т.д.). Объединение единиц соответствует операциям склеивания и поглощения. Иначе говоря, формируются максимальные подкубы.
4. Для каждого объединения выписываются конъюнкции из элементов, общих для каждой единицы, входящих в объединение..
5. Выше полученные конъюнкции составляют МДНФ.
Карты Вейча удобны при поиске МДНФ функций двух, трех и четырех переменных.
n=2
СДНФ= 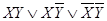
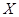 | 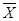 | |
 1 1 | 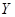 | |
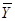 |
МДНФ= 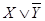
n=3
СДНФ= 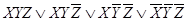
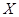 | 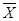 | |||
 1 1 | 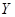 | |||
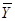 | ||||
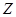 | 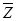 | 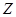 |
МДНФ= 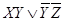
n=4
СДНФ= 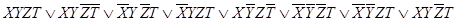
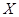 | 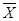  | ||||
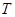 |  1 1 |  1 1 | 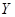 | ||
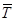 | |||||
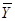 | |||||
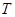 |  | ||||
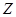 | 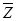 | 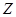 |
МДНФ= 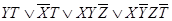
Задание на практическую работу:
Вариант 1
Задание 1.Построить таблицу истинности для функции
f(x,y,z)=(xy 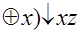
Задание 2. Определить, является ли данная функция алгебры логики тождественно ложной/истинной?
f(x,y,z)=(xy 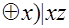
Задание 3. Выразить данную функцию через коньюкцию и дизъюнкцию?
f(x,y,z)=(xy 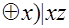 )
)
Задание 5.Упростить данную функцию используя элементарные преобразования
f(x,y,z)=(xy  z)(x|y)
z)(x|y)
Задание 6. Построить СДНФ для функции.
f(x,y,z)=(xy  z)
z) 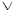 (xz
(xz 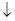 y)
y)
Задание 7. Построить СКНФ для функции.
f(x,y,z)=(xy  z)
z) 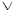 (xz
(xz 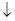 y)
y)
Вариант 2
Задание 1.Построить таблицу истинности для функции
f(x,y,z)=(xy 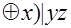
Задание 2. Определить, является ли данная функция алгебры логики тождественно ложной/истинной?
f(x,y)=(x  y)(y
y)(y 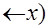 )
)
Задание 3. Выразить данную функцию через коньюкцию и дизъюнкцию?
f(x,y)=(x  y)(y
y)(y 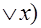 )
)
Задание 5.Упростить данную функцию используя элементарные преобразования
.
f(x,y)=(x  y)(y
y)(y 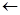 (x
(x  y))
y))
Задание 6. Построить СДНФ для функции.
f(x,y,z)=(xy 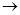 z)
z) 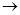 (xz
(xz 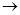 y)
y)
Задание 7. Построить СКНФ для функции.
f(x,y,z)=(xy 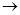 z)
z) 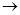 (xz
(xz 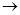 y)
y)
Вариант 3
Задание 1.Построить таблицу истинности для функции
f(x,y)=(xy  x)
x) 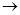 y
y
Задание 2. Определить, является ли данная функция алгебры логики тождественно ложной/истинной?
f(x,y,z)=xyz 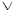
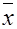
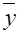
Задание 3. Выразить данную функцию через коньюкцию и дизъюнкцию?
f(x,y,z)=xyz 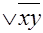
Задание 5.Упростить данную функцию используя элементарные преобразования
f(x,y,z)=(xyz 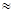 (x
(x  y))
y))  z
z
Задание 6. Построить СДНФ для функции.
f(x,y,z)=(x  z)
z) 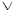 (x
(x  y)
y) 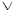 (y
(y  z)
z)
Задание 7. Построить СКНФ для функции.
f(x,y,z)=(x  z)
z) 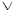 (x
(x  y)
y) 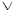 (y
(y  z)
z)
Технология работы
Задание №1Используя таблицы истинности для каждой из операций построить таблицу истинности для функции. Соблюсти лексикографический порядок, использовать все наборы логических значений переменных
Задание №2 Рассчитать логические значения функции на всех наборах переменных, сделать вывод
Задача№3 Используя тождественные преобразования перейти к формуле содержащей только конъюнкции и дизъюнкции (операция отрицания допустимо только применяемо к переменной).
Задача №4Поэтапно применять тождества алгебры логики, учитывая порядок выполнения операций.При их применении необходимо руководствоваться принципом упрощения(сокращение операции, замена более сложных на более простые, сокращение количества переменных)
Задание №5 В данной задачи применимы все 3 метода приведения к совершенной форме. Выбор метода зависит от простоты применения и способностей учащихся.
Задание №6 В данной задачи применимы все 3 метода приведения к совершенной форме. Выбор метода зависит от простоты применения и способностей учащихся.
Контрольные вопросы:
1.
Что называется высказыванием?
2.
Приведите пример высказываний. Какое высказывание называется истинным, а какое ложным?
3.
Что называется составным высказыванием?
4.
Перечислите виды логических операций над высказываниями и сформулируйте их определение.
5.
Какие основные символы используются в теории высказываний?
6.
Какие связки простейшие? Назовите другие связки.
7.
Что такое таблица истинности высказывания и как она строится? Как ещё называется эта таблица?
8.
Какие существуют логические отношения между высказываниями?
9.
Перечислите варианты импликации.
10.
Сформулируйте основные законы алгебры высказываний. Как их доказать?
11.
Что такое булева функция?
12.
Как строится таблица истинности для булевых функций?
13.
Что такое ДНФ и КНФ?
14.
Дайте определение совершенного одночлена.
15.
Приведите правило преобразования формул в СДНФ и СКНФ.
16.
Как булевы функции связаны с формулами алгебры высказываний?
17.
Дайте определение многочлена Жегалкина и сформулируйте теорему Жегалкина.
18.
Сформулируйте первый алгоритм построения многочлена Жегалкина булевой функции.
19.
В чём состоит метод неопределённых коэффициентов для построения многочлена Жегалкина?
20.
Какой многочлен Жегалкина называется не линейным?
21.
Каков алгоритм определения линейности (нелинейности) булевой функции?
