Количество часов, отводимых на выполнение практической работы 2ч
Тема:Решение задач по теме «Булева алгебра»
Цель:научитьсяприменять законы алгебры логики.
Общие теоретические сведения
Операции над высказываниями.
Отрицанием высказывания х называется новое высказывание, которое истинно, если высказывание ложное и наоборот. Таблица истинности операции отрицания имеет вид:
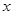 | 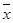 |
Дизъюнкцией двух высказываний x и y(логическое «или»)называется новое высказывание, которое будет истинным тогда когда, когда хотя бы одно из высказываний будет истинным.
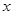 | 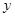 | 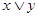 |
Конъюнкцией двух высказываний x и y(логическое «и»)называется новое высказывание, которое будет истинным тогда когда, когда оба высказывания истины. Обозначение операции конъюнкция - &( 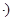
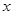 | 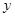 | 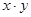 |
Импликацией двух высказываний x и y(«если – то») называется новое высказывание, которое ложно тогда, когда х(предпосылка)- истинно, а у(следствие)- ложно.
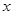 | 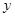 | 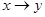 |
Эквивалентностью двух высказываний x и y(«тогда и только тогда») называется новое высказывание, которое будет истинно , если высказывания х и у будут одновременно истинны или ложны.
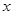 | 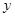 | 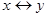 |
Неодназночностью (суммой по модулю два) двух высказываний x и y(«тогда и только тогда») называется новое высказывание, которое будет истинно тогда когда одно из высказываний х или у истинно, а другое ложно.
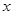 | 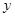 | 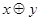 |
Штрих Шеффера (логическое «и - не») высказываний x и y - это новое высказывание, которое будет ложно тогда и только тогда когда оба высказывания истинны.
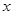 | 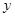 | 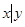 |
Стрелка Пирса (логическое «или - не») высказываний x и y - это новое высказывание, которое будет истинно тогда и только тогда когда оба высказывания ложны.
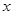 | 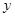 | 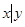 |
Для операций справедливы следующие приоритеты: ù, &, Ú, ®, «.
Формулы равносильности.
1) Коммутативность
АVВ º ВVА А&В º В&А
2) Ассоциативность
АV(ВVС) º (АVВ)VС А&(В&С) º (А&В) &С
3) Дистрибутивность
АV(В&С) º (АVВ)&(АVС) А&(ВVС) º (А&В)V(А&С)
4) Идемпотентность
АVА º А А&А º А
5) Поглощение
АV(А&В) º А А&(АVВ) º А
6) Закон де Моргана
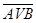 º
º 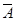 &
& 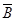
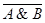 º
º 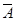 V
V 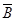
7) Закон исключающий третьего
АV1 º 1 А&1 º A
8) Закон противоречия
AVÆ º A A&Æ º Æ
9) Закон двойного отрицания
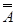 º A
º A
10) 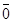 º 1 ,
º 1 , 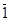 º 0
º 0
11) A®B º 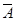 VB
VB
12) A«B º (A®B)&(B®A)
13) AÅB º A& 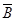 V
V 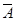 &B
&B
14) A | B º 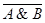 º
º 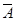 V
V 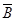
15) A¯B º 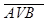 º
º 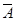 &
& 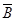
Дизъюнктивной нормальной формой (ДНФ) формулы  называется выражение вида:
называется выражение вида:
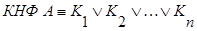 , (2.4)
, (2.4)
где 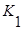 - элементарная конъюнкция.
- элементарная конъюнкция.
Конъюнктивной нормальной формой (КНФ) формулы  называется выражение вида:
называется выражение вида:
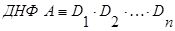 , (2.5)
, (2.5)
где 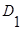 - элементарная дизъюнкция.
- элементарная дизъюнкция.
Любую формулу можно представить в виде ДНФ или КНФ.
ПРИМЕР
Пусть дана формула
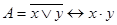
Требуется получить ДНФ и КНФ данной формулы.
Применяя формулы равносильности, получаем КНФ  :
:
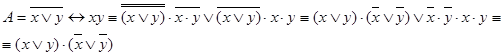
Применяя формулы равносильности, получаем ДНФ  :
:
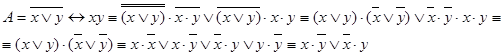
Совершеннойдизъюнктивной нормальной формой(СДНФ) формулы  называется такая ДНФ, для которой выполняются следующие условия:
называется такая ДНФ, для которой выполняются следующие условия:
1. Все элементарные конъюнкции, входящие в ДНФ  , различны.
, различны.
2. Все элементарные конъюнкции, входящие в ДНФ  , содержат литеры, соответствующие всем переменным.
, содержат литеры, соответствующие всем переменным.
3. Каждая элементарная конъюнкция, входящая в ДНФ  , не содержит двух одинаковых литер.
, не содержит двух одинаковых литер.
4. Каждая элементарная конъюнкция, входящая в ДНФ  , не содержит переменную и ее отрицание.
, не содержит переменную и ее отрицание.
СДНФ  можно получить двумя способами:
можно получить двумя способами:
1. по таблице истинности;
2. с помощью равносильных преобразований.
Совершеннойконъюнктивной нормальной формой(СКНФ) формулы  называется такая КНФ, для которой выполняются следующие условия:
называется такая КНФ, для которой выполняются следующие условия:
1. Все элементарные дизъюнкции, входящие в КНФ  , различны.
, различны.
2. Все элементарные дизъюнкции, входящие в КНФ  , содержат литеры, соответствующие всем переменным.
, содержат литеры, соответствующие всем переменным.
3. Каждая элементарная дизъюнкция, входящая в КНФ  , не содержит двух одинаковых литер.
, не содержит двух одинаковых литер.
4. Каждая элементарная дизъюнкция, входящая в КНФ  , не содержит переменную и ее отрицание.
, не содержит переменную и ее отрицание.
