По выполнению практических работ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ
длястудентов 2 курса
специальности
Информационные системы (по отраслям)
Программирование в компьютерных системах
Нижний Новгород
2015г.
| РАССМОТРЕНО на заседании ПЦК Протокол № ___ от _____________ Председатель ПЦК ________ __________ подпись | УТВЕРЖДАЮ Заместитель руководителя СПО по УМР _ _________ Л.Ю. Шалыминова подпись | |
| Составитель:Базин Е.С. преподаватель математических дисциплин. |
Содержание:
Практическая работа № 1 стр 4
Практическая работа №2 стр 11
Практическая работа №3 стр 22
Практическая работа №4 стр 34
Практическая работа № 1
Количество часов, отводимых на выполнение практической работы 2ч
Тема:Решение задач по теме «Теория множеств»
Цель:закреплениеосновных понятий теории множеств, теоретико-множественных операций.
Теоретические сведения:
Свойства подмножеств.
1. Рефлексивность. Множество А является подмножеством множества А:
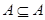 . (2)
. (2)
2. Транзитивность. Если множество А является подмножеством множества В , а множество В является подмножеством множества С, то множество А является подмножеством множества С:
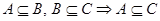 (3)
(3)
3. Принцип объемности. Если множество А является подмножеством множества В, а множество В является подмножеством множество А, то множество А равно множеству В:
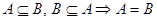 (4)
(4)
Операции над множествами.
1. Объединением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В:
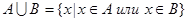 (5)
(5)
2. Пересечениеммножеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат множеству А и множеству В:
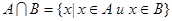 (6)
(6)
3. Разностьюмножества А и В называется множество всех тех элементов, которые принадлежат множеству А и не принадлежат множеству В:
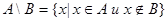 (7)
(7)
4. Симметричной разностьюмножеств А и В называется множество , состоящее из элементов множества А , не принадлежащих множеству В, и элементов множества В, не принадлежащих множеству А:
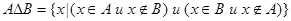 (8)
(8)
5. Дополнениеммножества А называется множество всех тех элементов, которые не принадлежат множеству А:
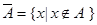
Алгебра теории множеств.
Для любых множеств А, В и С выполнимы следующие тождества:
1. Коммутативный закон
 (9)
(9)
2. Ассоциативный закон
 (10)
(10)
3. Дистрибутивный закон
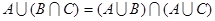
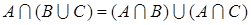 (11)
(11)
4. Закон поглощения
 (12)
(12)
5. Закон идемпотентности
 (13)
(13)
6. Закон де Моргана
 (14)
(14)
7. Закон исключенного третьего
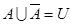 (15)
(15)
8. Закон противоречия
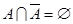 (16)
(16)
9. Операции с универсумом:
 (17)
(17)
10. Операции с пустым множеством:
 (18)
(18)
11.  (19)
(19)
12. Закон двойного дополнения
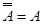 (20)
(20)
13. 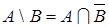 (21)
(21)
14. 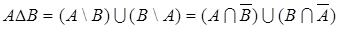 (22)
(22)
Основные свойства отношений.
1. Рефлексивность.
Отношение называется рефлексивным, если для всех x выполняется условие: xjx или DMÍF.
Антирефлексивность.
Отношение называется антирефлексивным, если для всех x выполняется условие: ùxjx (символ “ù“ означает “не выполняется”) или 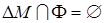 .
.
3. Симметричность.
Отношение называетсясимметричным , если для всех x выполняется условие: xjy Þ yjx или Ф=Ф-1.
Антисимметричность.
Отношение называется антисимметричным, если для всех x выполняется условие: xjy и x¹y Þù yjx или 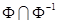 ÍDM.
ÍDM.
Асимметричность.
Отношение называется асимметричным, если для всех x выполняется условие: xjy Þù yjx или 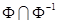 =Æ.
=Æ.
6. Связность (полнота).
Отношение называется связным (полным), если для всех x выполняется условие: x¹y Þ xjy или yjx или М2\DMÍ 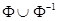 .
.
Транзитивность.
Отношение называется транзитивным, если для всех x выполняется условие: xjy и yjz Þ xjz или Ф 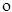 ФÍФ.
ФÍФ.
Задание на практическую работу:
Вариант №1
1. Даны множества:
A = {5, 6, 7, 8, 9, 10, 11, 12},
B = {x / x<11, x – натуральное число},
C = {x / 7<x<14, x – натуральное число};
1) Изобразить эти множества
2) Перечислить элементы множества АÈВÇС.
2. Найдите çPç, где P = 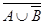 если:
если:
U={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {0, 2, 4, 6};
B = {3, 5, 7, 8, 9}
3. Упростить выражение:
AÇBÇBÇCÇ( 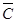 ÈAÇB)ÇCÈC;
ÈAÇB)ÇCÈC;
4. Решить уравнение:
AX∆B=B\X
5. Дать анкету бинарного отношения:
aФb: a-b делится на 2
Вариант №2
1. Даны множества:
A = {5, 6, 7, 8, 9, 11},
B = {x / x<8, x – натуральное число},
C = {x / 1<x<13, x – натуральное число};
1) Изобразить эти множества
2) Перечислить элементы множества АÈВÇС.
2. Найдите çPç, где P = 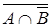 если:
если:
U={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {0, 2, 4, 6};
B = {3, 5, 7, 8, 9}
3. Упростить выражение:
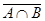 ÇBÇCÇ(
ÇBÇCÇ( 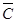 ÈA)ÇBÇCÈC;
ÈA)ÇBÇCÈC;
4. Решить уравнение:
BX=(A\X)B
5. Дать анкету бинарного отношения:
aФb: a>2b
Вариант №3
1. Даны множества:
A = {1, 2, 3, 4, 5, 6},
B = {x / x<8, x – целое число},
C = {x / 1<x<15, x – натуральное четное число};
1) Изобразить эти множества
2) Перечислить элементы множества АÈВÇС.
2. Найдите çPç, где P = 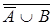 если:
если:
U={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {0, 2, 5, 6};
B = {3, 5, 7, 8, 9}
3. Упростить выражение:
( 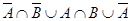 )ÇCÇB
)ÇCÇB
4. Решить уравнение:
AX∆B=X\A
5. Дать анкету бинарного отношения:
aФb: a=b+3
Технология работы:
Задание№1
Используя основные свойства множеств и определение подмножества выполнить задание.
Для изображения множеств использовать или диаграммы Эйлера или числовую прямую
Задание №2
Используя определение мощности множества выполнить задание.
Задание №3
Для выполнения данного задания необходимо последовательно применять тождества алгебры множеств. При их применении необходимо руководствоваться принципом упрощения(сокращение операции, замена более сложных на более простые, сокращение количества переменных)
Задание №4
Используя алгоритм решения, решить его
Задание №5
Последовательно исследовать данное соответствие на все свойства соответствий, сделать вывод
7 Контрольные вопросы
1. Дайте определения: а) пересечения множеств; б) объединения множеств; в) разности двух множеств; г) дополнения множества А до множества В; д) декартова произведения множеств. Как называются соответствующие операции над множествами?
2. Как с помощью кругов Эйлера изобразить а) пересечение множеств; б) объединение множеств; в) разность двух множеств; г) дополнение множества А до множества В?
3. Назовите основные свойства операций пересечения и объединения множеств.
4. Каков порядок действий в формулах, содержащих несколько теоретико-множественных операций, если формулы
а) не содержат скобок; б) содержат скобки?
5. Как изображается на координатной плоскости декартово произведение двух числовых множеств? Приведите примеры.
6. Дайте определение соответствия между множествами XиY. Приведите примеры соответствий.
7. Назовите способы задания соответствий.
8. Что такое граф соответствия; график соответствия?
9. Дайте определение обратного соответствия.
10. Какое соответствие называется взаимно однозначным?
11. Какие множества называются равномощными? Приведите примеры равномощных множеств.
12. Дайте определение бинарного отношения на множестве Х. Приведите примеры отношений.
13. В чем состоит свойство
а) рефлексивности;
б) симметричности;
в) антисимметричности;
г) транзитивности;
д) связанности
отношения? Какова особенность графа отношения в каждом из случаев?
14. Дайте определения отношений эквивалентности и порядка. Приведите примеры таких отношений.
Список рекомендуемой литературы
1. Дискретная математика: Учебное пособие / С.А. Канцедал. - М.: ИД ФОРУМ, НИЦ ИНФРА-М, 2014. - 224 c.
2. Дискретная математика: Учебник для студ. учреждений сред. проф. образования / М. С. Спирина, П. А. Спирин. — М.: Издательский центр «Академия», 2013. — 368 с.
Практическая работа № 2
Формулы равносильности.
1) Коммутативность
АVВ º ВVА А&В º В&А
2) Ассоциативность
АV(ВVС) º (АVВ)VС А&(В&С) º (А&В) &С
3) Дистрибутивность
АV(В&С) º (АVВ)&(АVС) А&(ВVС) º (А&В)V(А&С)
4) Идемпотентность
АVА º А А&А º А
5) Поглощение
АV(А&В) º А А&(АVВ) º А
6) Закон де Моргана
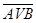 º
º 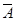 &
& 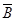
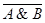 º
º 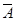 V
V 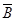
7) Закон исключающий третьего
АV1 º 1 А&1 º A
8) Закон противоречия
AVÆ º A A&Æ º Æ
9) Закон двойного отрицания
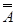 º A
º A
10) 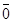 º 1 ,
º 1 , 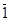 º 0
º 0
11) A®B º 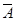 VB
VB
12) A«B º (A®B)&(B®A)
13) AÅB º A& 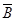 V
V 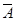 &B
&B
14) A | B º 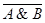 º
º 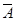 V
V 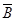
15) A¯B º 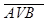 º
º 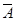 &
& 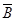
Дизъюнктивной нормальной формой (ДНФ) формулы  называется выражение вида:
называется выражение вида:
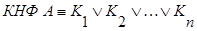 , (2.4)
, (2.4)
где 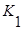 - элементарная конъюнкция.
- элементарная конъюнкция.
Конъюнктивной нормальной формой (КНФ) формулы  называется выражение вида:
называется выражение вида:
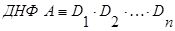 , (2.5)
, (2.5)
где 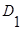 - элементарная дизъюнкция.
- элементарная дизъюнкция.
Любую формулу можно представить в виде ДНФ или КНФ.
ПРИМЕР
Пусть дана формула
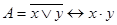
Требуется получить ДНФ и КНФ данной формулы.
Применяя формулы равносильности, получаем КНФ  :
:
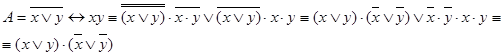
Применяя формулы равносильности, получаем ДНФ  :
:
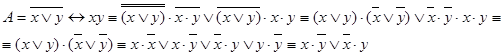
Совершеннойдизъюнктивной нормальной формой(СДНФ) формулы  называется такая ДНФ, для которой выполняются следующие условия:
называется такая ДНФ, для которой выполняются следующие условия:
1. Все элементарные конъюнкции, входящие в ДНФ  , различны.
, различны.
2. Все элементарные конъюнкции, входящие в ДНФ  , содержат литеры, соответствующие всем переменным.
, содержат литеры, соответствующие всем переменным.
3. Каждая элементарная конъюнкция, входящая в ДНФ  , не содержит двух одинаковых литер.
, не содержит двух одинаковых литер.
4. Каждая элементарная конъюнкция, входящая в ДНФ  , не содержит переменную и ее отрицание.
, не содержит переменную и ее отрицание.
СДНФ  можно получить двумя способами:
можно получить двумя способами:
1. по таблице истинности;
2. с помощью равносильных преобразований.
Совершеннойконъюнктивной нормальной формой(СКНФ) формулы  называется такая КНФ, для которой выполняются следующие условия:
называется такая КНФ, для которой выполняются следующие условия:
1. Все элементарные дизъюнкции, входящие в КНФ  , различны.
, различны.
2. Все элементарные дизъюнкции, входящие в КНФ  , содержат литеры, соответствующие всем переменным.
, содержат литеры, соответствующие всем переменным.
3. Каждая элементарная дизъюнкция, входящая в КНФ  , не содержит двух одинаковых литер.
, не содержит двух одинаковых литер.
4. Каждая элементарная дизъюнкция, входящая в КНФ  , не содержит переменную и ее отрицание.
, не содержит переменную и ее отрицание.
Вариант 1
Задание 1.Построить таблицу истинности для функции
f(x,y,z)=(xy 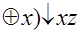
Задание 2. Определить, является ли данная функция алгебры логики тождественно ложной/истинной?
f(x,y,z)=(xy 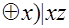
Задание 3. Выразить данную функцию через коньюкцию и дизъюнкцию?
f(x,y,z)=(xy 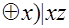 )
)
Задание 5.Упростить данную функцию используя элементарные преобразования
f(x,y,z)=(xy  z)(x|y)
z)(x|y)
Задание 6. Построить СДНФ для функции.
f(x,y,z)=(xy  z)
z) 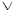 (xz
(xz 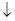 y)
y)
Задание 7. Построить СКНФ для функции.
f(x,y,z)=(xy  z)
z) 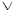 (xz
(xz 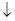 y)
y)
Вариант 2
Задание 1.Построить таблицу истинности для функции
f(x,y,z)=(xy 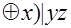
Задание 2. Определить, является ли данная функция алгебры логики тождественно ложной/истинной?
f(x,y)=(x  y)(y
y)(y 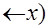 )
)
Задание 3. Выразить данную функцию через коньюкцию и дизъюнкцию?
f(x,y)=(x  y)(y
y)(y 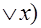 )
)
Задание 5.Упростить данную функцию используя элементарные преобразования
.
f(x,y)=(x  y)(y
y)(y 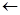 (x
(x  y))
y))
Задание 6. Построить СДНФ для функции.
f(x,y,z)=(xy 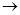 z)
z) 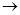 (xz
(xz 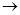 y)
y)
Задание 7. Построить СКНФ для функции.
f(x,y,z)=(xy 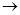 z)
z) 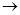 (xz
(xz 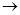 y)
y)
Вариант 3
Задание 1.Построить таблицу истинности для функции
f(x,y)=(xy  x)
x) 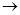 y
y
Задание 2. Определить, является ли данная функция алгебры логики тождественно ложной/истинной?
f(x,y,z)=xyz 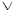
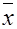
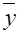
Задание 3. Выразить данную функцию через коньюкцию и дизъюнкцию?
f(x,y,z)=xyz 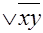
Задание 5.Упростить данную функцию используя элементарные преобразования
f(x,y,z)=(xyz 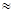 (x
(x  y))
y))  z
z
Задание 6. Построить СДНФ для функции.
f(x,y,z)=(x  z)
z) 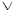 (x
(x  y)
y) 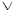 (y
(y  z)
z)
Задание 7. Построить СКНФ для функции.
f(x,y,z)=(x  z)
z) 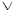 (x
(x  y)
y) 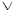 (y
(y  z)
z)
Технология работы
Задание №1Используя таблицы истинности для каждой из операций построить таблицу истинности для функции. Соблюсти лексикографический порядок, использовать все наборы логических значений переменных
Задание №2 Рассчитать логические значения функции на всех наборах переменных, сделать вывод
Задача№3 Используя тождественные преобразования перейти к формуле содержащей только конъюнкции и дизъюнкции (операция отрицания допустимо только применяемо к переменной).
Задача №4Поэтапно применять тождества алгебры логики, учитывая порядок выполнения операций.При их применении необходимо руководствоваться принципом упрощения(сокращение операции, замена более сложных на более простые, сокращение количества переменных)
Задание №5 В данной задачи применимы все 3 метода приведения к совершенной форме. Выбор метода зависит от простоты применения и способностей учащихся.
Задание №6 В данной задачи применимы все 3 метода приведения к совершенной форме. Выбор метода зависит от простоты применения и способностей учащихся.
Контрольные вопросы:
1.
Что называется высказыванием?
2.
Приведите пример высказываний. Какое высказывание называется истинным, а какое ложным?
3.
Что называется составным высказыванием?
4.
Перечислите виды логических операций над высказываниями и сформулируйте их определение.
5.
Какие основные символы используются в теории высказываний?
6.
Какие связки простейшие? Назовите другие связки.
7.
Что такое таблица истинности высказывания и как она строится? Как ещё называется эта таблица?
8.
Какие существуют логические отношения между высказываниями?
9.
Перечислите варианты импликации.
10.
Сформулируйте основные законы алгебры высказываний. Как их доказать?
11.
Что такое булева функция?
12.
Как строится таблица истинности для булевых функций?
13.
Что такое ДНФ и КНФ?
14.
Дайте определение совершенного одночлена.
15.
Приведите правило преобразования формул в СДНФ и СКНФ.
16.
Как булевы функции связаны с формулами алгебры высказываний?
17.
Дайте определение многочлена Жегалкина и сформулируйте теорему Жегалкина.
18.
Сформулируйте первый алгоритм построения многочлена Жегалкина булевой функции.
19.
В чём состоит метод неопределённых коэффициентов для построения многочлена Жегалкина?
20.
Какой многочлен Жегалкина называется не линейным?
21.
Каков алгоритм определения линейности (нелинейности) булевой функции?
Основные понятия теории графов
Графом называется пара следующего вида:
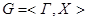 , (3.1)
, (3.1)
где  - график
- график  ;
;
 - множество вершин.
- множество вершин.
Иными словами, граф представляет совокупность множества вершин и дуг.
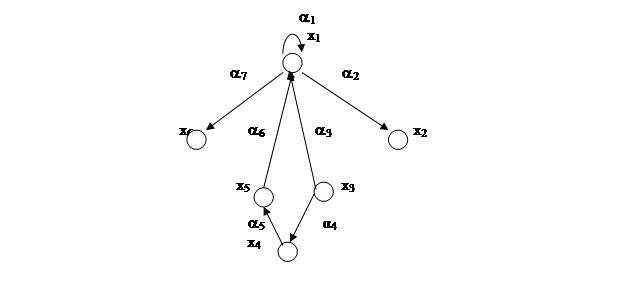 |
Рис. 3.2. Граф
Граф, представленный на рис. 3. 2, состоит из множества вершин 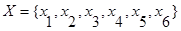
 и множество дуг
и множество дуг 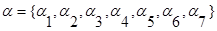
Графическое изображение графа является самым наглядным, но не единственным способом задания графа. Кроме того граф может быть задан:
1. перечислением:
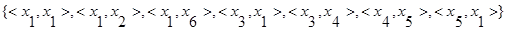
2. множеством образов:
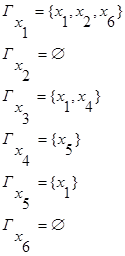 ,
,
где 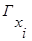 - образ вершины
- образ вершины 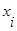 - множество вершин, в которые исходят дуги из данной вершины.
- множество вершин, в которые исходят дуги из данной вершины.
Матрицей инцидентности
Матрица инцидентности - это матрица вершин и инцидентных им дуг.
Дуга инцидентнавершине, если эта дуга исходит или заходит в данную вершину.
Вершина инцидентнадуге, если в эту вершину заходит или исходит данная дуга.
В матрице инцидентности в первом столбце расположены вершины, в первой строке – дуги. Остальные ячейки матрицы инцидентности заполняются по следующему правилу:
· 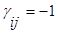 , если из i-той вершины исходит j-тая дуга:
, если из i-той вершины исходит j-тая дуга:
· 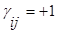 , если в i-той вершину заходит j-тая дуга;
, если в i-той вершину заходит j-тая дуга;
· 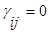 , если i-тая вершина не инцидента j-той дуге;
, если i-тая вершина не инцидента j-той дуге;
· 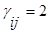 , если из i-той вершины исходит j-тая дуга и в нее же заходит, т.е. в i-той вершине j-тая дуга образует петлю.
, если из i-той вершины исходит j-тая дуга и в нее же заходит, т.е. в i-той вершине j-тая дуга образует петлю.
Для графа, представленного на рис. 3.2 матрица инцидентности имеет вид:
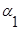 | 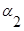 | 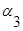 | 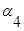 | 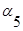 | 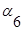 | 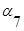 | |
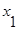 | -1 | +1 | +1 | -1 | |||
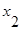 | +1 | ||||||
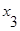 | -1 | -1 | |||||
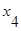 | +1 | -1 | |||||
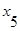 | +1 | -1 | |||||
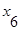 | +1 |
На практике в матрице инцидентности иногда нули не проставляются для наглядности.
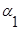 | 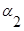 | 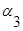 | 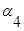 | 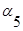 | 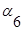 | 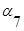 | |
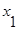 | -1 | +1 | +1 | -1 | |||
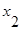 | +1 | ||||||
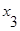 | -1 | -1 | |||||
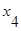 | +1 | -1 | |||||
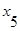 | +1 | -1 | |||||
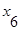 | +1 |
Свойство матрицы инцидентности – сумма элементов по столбцам равна 0 или 2.
Матрицей смежности
Смежные дуги – это дуги инцидентные одной вершине.
Смежные вершины – вершины, инцидентные одной дуге.
Матрица смежности - это матрица смежных вершин.
Матрица смежности заполняется по следующему правилу: 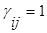 , если из i-той вершины исходит дуга в j – тую вершину; во всех остальных случаях
, если из i-той вершины исходит дуга в j – тую вершину; во всех остальных случаях 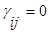 (для удобства и наглядности на практике в матрице смежности нули не проставляются).
(для удобства и наглядности на практике в матрице смежности нули не проставляются).
Для графа, представленного на рис. 3.2 матрица смежности имеет вид:
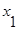 | 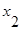 | 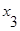 | 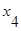 | 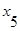 | 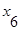 | |
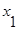 | ||||||
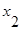 | ||||||
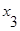 | ||||||
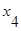 | ||||||
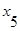 | ||||||
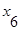 |
Полустепенью захода 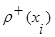 i–той вершины называется число дуг, заходящих в данную вершину.
i–той вершины называется число дуг, заходящих в данную вершину.
Полустепенью исхода 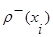 i-той вершины называется число дуг, исходящих из данной вершины.
i-той вершины называется число дуг, исходящих из данной вершины.
Степенью i-той вершины исхода 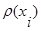 называется сумма полустепеней захода и исхода:
называется сумма полустепеней захода и исхода:
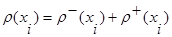 (3.2)
(3.2)
Свойства матрицы смежности:
1. Сумма единиц по строке определяет полустепень исхода;
2. Сумма единиц по столбцу определяет полустепень захода;
3. Сумма единиц по строкам и по столбцам определяет степень вершин.
Основное свойство графа:
В любых графах число вершин с нечетной степенью четно.
Путемв графе называется последовательность дуг такая, что каждая следующая дуга исходит из вершины, в которую заходит предыдущая дуга.
Длиной путиназывается количество пройденных дуг.
Простой путь – это такой путь, в котором дуга встречается не более одного раза.
Элементарный путь – это путь, в котором вершина встречается не более одного раза.
Контур – путь, начинающийся и заканчивающийся в одной точке.
Петля – контур длиной в одну единицу.
Графы бывают двух видов:
· ориентированный граф (орграф) - это граф, состоящий из вершин и дуг.
· неориентированный граф – это граф, состоящий из вершин и ребер. Ребро – это дуга, не имеющая направление.
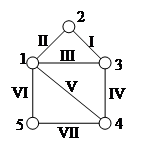
Рис. 3.3. Неориентированный граф
В неориентированном графе путь называется цепью; контур – циклом.
Неориентированный граф также может быть задан с помощью матриц инцидентности и смежности.
Матрица инцидентности для неориентированного графа составляется по правилу:
· 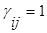 , если i-тая вершина инцидентна j-тому ребру;
, если i-тая вершина инцидентна j-тому ребру;
· 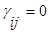 , если i-тая вершина не инцидента j-тому ребру;
, если i-тая вершина не инцидента j-тому ребру;
· 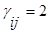 , если. в i-той вершине j-тое ребро образует петлю.
, если. в i-той вершине j-тое ребро образует петлю.
Для графа, представленного на рис. 3.3, матрица инцидентности имеет вид:
| I | II | III | IV | V | VI | VII | |
Матрица смежности для неориентированного графа составляется по правилу: 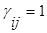 , если из i-тая и j – тая вершины смежные.
, если из i-тая и j – тая вершины смежные.
Для графа, представленного на рис. 3.3, матрица смежности имеет вид:
Матрица смежности для неориентированного графа симметрична относительно главной диагонали. Степень i- той вершины равна сумме элементов по строке или по столбцу матрицы смежности.
Если в графе присутствуют как ребра, так и дуги, то он называется смешанным.
Если между двумя вершинами существует более чем 1 дуга или ребро, то такой граф называется мультиграфом.
 |
Рис. 3.4. Смешанный мультиграф.
Граф называется связным, если между любыми двумя вершинами которого существует путь (цепь).
Эйлеров граф.
Эйлеровой цепьюназывается цепь, проходящая по всем ребрам графа.
Эйлеровым циклом называется эйлеровая цепь, начинающаяся и заканчивающаяся в одной вершине.
Эйлеровым графомназывается граф, содержащий Эйлеров цикл.
ТЕОРЕМА: Для того чтобы связанный граф был Эйлеровым, необходимо и достаточно, чтобы степени всех вершин были четны
Данная теорема позволяет решить задачу о Кенигсбергских мостах. Граф, соответствующий данной задаче, имеет вид
А
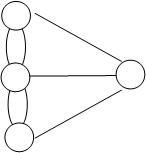 |
С D
B
Рис. 3.5 Граф «Кенигсбергские мосты»
Вершины графа (A, B, C, D) имеют степени:
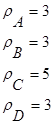 (3.3)
(3.3)
Тогда в соответствии с теоремой Эйлера данный граф не является Эйлеровым. А это означает, что нельзя обойти все мосты г. Кенигсберга строго по одному разу, начав и закончив путь в одной точке суши.
Следствие из ТЕОРЕМЫ: Для того чтобы граф содержал Эйлеровую цепь, необходимо и достаточно, чтобы две вершины имели нечетную степень. При этом в одной из вершин цепь будет начинаться, в другой – заканчиваться.
Алгоритм фронта волны.
Пусть необходимо найти минимальный путь из вершины 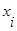 в вершину
в вершину 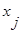 .
.
1. Выписываются все вершины с 1 по n. Вершина  помечается индексом 0.
помечается индексом 0.
2. Находится первый фронт волны 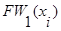 как множество вершин образа вершины
как множество вершин образа вершины 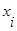 .
.
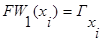 (3.17)
(3.17)
3. Все вершины, принадлежащие первому фронту волны, помечаются индексом 1.
4. Вводится счетчик шагов (фронтов волны) 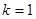 .
.
5. Если 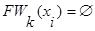 или
или 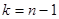 , то вершина
, то вершина 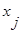 недостижима из вершины, и работа алгоритма на этом заканчивается. В противном смысле переходим к пункту 6.
недостижима из вершины, и работа алгоритма на этом заканчивается. В противном смысле переходим к пункту 6.
6. Если 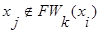 , то переходим к пункту 8. В противном случае существует путь из вершины
, то переходим к пункту 8. В противном случае существует путь из вершины 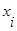 в вершину
в вершину 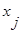 длиной в
длиной в 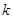 единиц, и этот путь минимальный:
единиц, и этот путь минимальный:
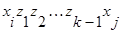
7. Находятся промежуточные вершины 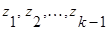 z по правилу:
z по правилу:

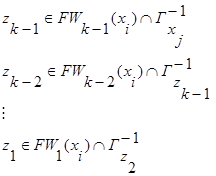 , (3.18)
, (3.18)
где 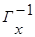 - прообраз вершины
- прообраз вершины 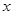 - множество вершин, из которых заходят дуги в вершину
- множество вершин, из которых заходят дуги в вершину 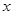
8. Определяется 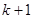 фронт волны как все непомеченные вершины, принадлежащие образу вершин
фронт волны как все непомеченные вершины, принадлежащие образу вершин 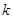 - го фронта волны. Помечаются индексом
- го фронта волны. Помечаются индексом 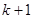 вершины
вершины 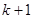 фронта волны. Далее осуществляется переход к пункту 5.
фронта волны. Далее осуществляется переход к пункту 5.
Задание №1.
Найти Эйлерову цепь в неориентированном графе.
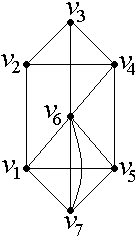 | 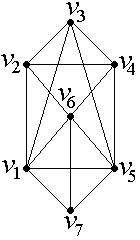 | 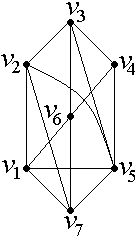 |
| а) | б) | в) |
Задание №2.Для графа G=(V,E), с заданными мощностями |V|=n, |E|=m составьте матрицы смежности и инцидентности, опр
