Вероятностные и энтропийные модели информационно-психологических операций и атак террористического характера

Пусть социотехническая система 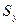подвергается террористическим атакам со стороны 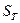- системы террористических организации. При этом спектр террористических актов характеризуется множеством:

T = { },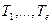

имеющих стохастический характер и характеризующихся соответствующими множествами вероятностей «успеха» и «не успеха» реализации теракта:

P(T) = ,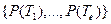

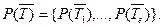
Соответственно, объект террористической атаки 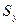в свою очередь характеризуется множеством возможных состояний (векторов переменных состояния):

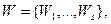
которые также носят вероятностный характер:

.

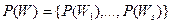Рассмотрим далее стохастический процесс взаимодействия 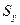и , и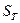спользуя в качестве функции полезности вероятность и энтропию.

При этом можно говорить о конфликте случайных событий, заключающихся в достижении некоторых целевых состояний. Тогда, если W и Т – совместимые зависимые случайные события, заключающиеся в достижении целевых состояний стохастическими системам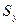и и 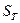соответственно, то в соответствии определениям террористического конфликта можно записать следующие неравенства для условных вероятностей:

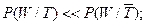
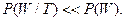
Степень связи между зависимыми событиями W и T предлагается оценивать в виде нормированного коэффициента R_WT свойства которого аналогичны свойствам парного коэффициента корреляции для случайных величин. Этот коэффициент назван коэффициентом корреляции событий

R_WT= [P(W/T)-P(W)P(T)]/√(P(W)[1-P(W)]P(T)[1-P(T)]

Преобразуем числитель в (4.4.20):

P(W/T)-P(W)P(T)=P(T)P(W\T)-P(W)P(T)=P(T)[P(W/T)-P(W)],

следовательно R_WT<0.

Для террористических акций R_WT<<0. Представленные выше соотношения достаточно точно характеризуют вероятности конфликта между атакуемой социотехнической системой S_Y(W) и атакующей её террористической системой S_T(T).

Устранение конфликта связано с изменением окружения, с формированием функциональных, параметрических и других преобразований. Разрешение конфликта связано с изменением элементов окружения 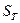систем 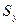таким образом, чтобы обеспечить устранений условий конфликта.

Также можно говорить о решении конфликта, связанным с выбором и построением различных схем компромисса и оптимизации. Хотя компромиссы с террористами мало продуктивны.

Рассмотрим две случайные величины W и T, характеризующие поведение стохастической системы S_Y. Из вышеизложенного следует, что между случайными величинами W и T наблюдается конфликт тогда и только тогда, когда значимое значение выборочного коэффициента корреляции r_XY меньше нуля. Для террористического конфликта это значение существенно меньше нуля.

Предположим, что две системы S_Y и S_T в процессе достижения своих целей W и T взаимодействуют в некоторой среде S (мировое сообщество) с общей целью.

Для анализа конфликта функционирующих стохастических систем необходима количественная мера. Поскольку конфликт определяет степень развития противоречия, вытекающего из организованности или неорганизованности, распознаваемости или не распознаваемости состояний системы, то в качестве такой меры уместно использовать энтропию системы.

Энтропия системы Н(S_Y) обладает следующими свойствами:

1. Энтропия системы Н(S_Y)=0, когда одно из состояний a_i достоверно, а другие невозможны.

2. Н(S_Y) при заданном числе состояний n достигает максимума, когда эти состояния равновероятны: P(W₁)=P(W₂)=…=P(W_S), а при увеличении S Н(S_Y) возрастает.

3 . Н(S_Y) обладает свойством аддитивности.

Мера энтропии системы S_Y определяется при этом следующим образом:

Н(S_Y)= -∑ P(W_i)log₂P(W_i). Энтропия системы S_Y при атаке S_T определяется как

H(W/T)=∑∑P(T_k)P(W_i/T_k)log2P(T_k/W_i).

Отметим, что согласно известной формуле Байеса P(T_k/W_i)=P(T)P(W_i/T_k)/∑P(T_j)P(W_i/T_k) энтропия может быть просчитана лишь через введенные ранее вероятности.

Исходя из выше изложенного, в качестве меры зависимости между системами S_Y и S_T может служить функционал информации

J(W,T)=H(W)-H(W/T)

или J(W,T)=H(W/T)-H(W) для оценки террористической деятельности, который показывает, насколько изменяет связанная с S_Y неопределенность от предварительного осуществления S_T.

В теории информации известны следующие соотношения, связывающие различные виды энтропии:

H(W,T)= H(W) + H(T/W)=H(T) + H(T/W), H(W) +H(T),

J(W/T)=H(W) + H(T)-H(W,T)=H(W)-H(W/T)=H(T)-H(T/W).

Наряду с абсолютной мерой зависимости о ввести нормированную меру зависимости между S_Y и S_T

N(W,T)=J(W,T)/H(W).

Эта мера обладает следующими свойствами:

1. N(W,T)=0, если системы S_Y и S_T независимы

2. N(W,T)=1, когда любое состояние Wkсистемы S_Y определяется поведением систем S_T, то есть реализацией одного из состояний T_j.

3 . Наряду с этим экстренными значениями N(W,T) принимает значения из интервала [0,1], которые характеризуют степень зависимости систем.

4. В общем случае N(W,T)≠N(T,W).

Хронологически энтропийные характеристики террористического акта иллюстрирует рис. 4.13.

Рис. 4.13. Кривая зависимости энтропии системы, атакуемой террористами, от времени

Здесь в период реализации теракта происходит вброс энтропии в систему из системы. Причем величина выброса зависит от чувствительности атакуемого объекта в системе. Целью террориста является значительное превышение по сравнению с уровнем фона. Значительная дезорганизация атакуемой системы через эпидемию страха — задача террористических операций и атак. В свою очередь стоит задача как можно более снизить всплеск энтропии и сократить период последействия.

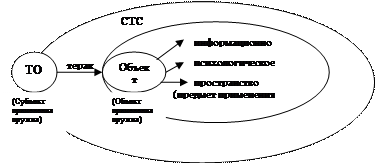
Принципиальным будем считать утверждение о том, что собственно теракт есть прежде всего детонатор для информационно-психологической бомбы (эффект последствия теракта), дестабилизирующей и дезоганизующей (значительно увеличивающей энтропию) атакуемое общество. Террористическая организация (ТО), выступая субъектом применения оружия, реализует теракт в отношении объекта применения оружия (объекта теракта) на стыке технической и социальной подсистем атакуемой социотехнической системы (СТС). Однако предметом атаки выступает уже информационно-психологическое пространство (ИПП), а точнее его энтропия – статический индикатор устойчивости СТС. Вышеизложенное иллюстрирует рис. 4.14, где ИПП выступает средой реакции на теракт.

	Рис 4.14. Обобщенная модель террористической атаки социотехнической системы

Рассмотрим процессы, активизируемые терактом в информационно-психологическом пространстве СТС, для которых прежде всего характерно:

1. Цепная реакция распространения цепного импульса на основе двух эффектов:

– первичного, т.е. успеха непосредственного воздействия на человека от информационного первоисточника;

– вторичного и более высокого порядка, т.е. в результате передачи информационного импульса от одного человека к другому.

При этом успех деструктивного информационно-управляющего воздействия ДИУВ состоит в устрашении отдельно взятой личности, поражающего дезорганизацией общества и государства.

2. Находясь на пороге создания глобального информационного общества, человечество сформировало разветвленную транснациональную информационно-коммуникационную среду, электронные средства массовой информации которой автоматически являются распространителем вышеупомянутого ИУВ практически без каких либо ограничений

Введем обозначения:

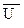– нормированный ущерб от реализации атак {Х};

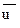– элементарный нормированный ущерб из множества ;

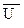R_isk - значение риска, зависимое от величины ;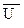

r_isk - элементарный риск из множества R_isk;

u_o - элементарный ущерб личности от одной реализация атаки;

p_o=p(u_o) -• элементарная вероятность нанесения ущерба от одной реализации угрозы ДИУВ (0<р<1);

q(u_o)=l-p(u_o) - вероятность (неуспеха) ДИУВ отсутствия нанесения ущерба от одной реализации атаки А_j;

n – количество личностей, подвергающихся атаки.

По биномиальному закону распределены вероятности наступления события точно k раз в п испытаниях Бернулли (то есть независимых и имеющих два исхода: '"успех", "неуспех"), в нашем случае событие - это реализация атаки Ti с нанесением ущерба u_o, вероятность чего равна р_о.

Результатом единичной атаки (одного события) является элементарный ущерб Uo, а результатом нескольких успешных событий будет ущерб U=ku_o. To есть закон дискретного распределения вероятностей наступления ущерба в общем виде имеет вид

Р = P(k,n, p_o) и U_o=ku_o.

Вероятность P_n(k) для биномиального распределения определяется по формуле Бернулли, которая описывает данное распределение:

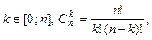
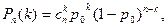
где 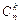– число всех сочетаний из n элементов по k.

Дальнейшее нормирование по максимально допустимому ущербу u_max=nu₀ переводит анализ в единичное пространство. Тогда k успехов из n подверженных ДИУВ имеет

.

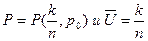Один из подходов оценки риска – это оценка произведений возможных ущербов, взвешенных с учётом их вероятностей. Отсюда проведём оценку риска и защищённости атакуемой системы. Из подверженных ДИУВ при количестве успехов k

На основании биномиального распределения вероятностей наступления ущерба получим риск

.

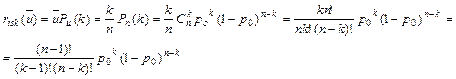
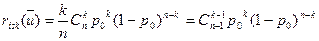Защищённость системы (эффективность защиты) можно оценить по относительному и абсолютному показателям.

Абсолютный показатель защищённости:

.

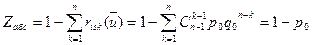Относительный показатель защищённости:

.

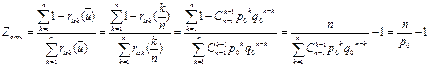По данной формуле увеличение параметра n и уменьшение p₀ приводит к возрастанию защищённости, уменьшение n и увеличение p₀ к его снижению.

Соответственно для нескольких групп ДИУВ n_i, i=1(1)N мы будем иметь свои элементарные вероятности p_0i. Такой разбивкой множества объектов управления мы можем существенно повысить точность описания процесса ДИУВ. Матожидание при таком разбиении будет равно сумме

M=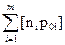

при мощности множества объектов воздействия

N= .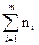

Эффективность ДИУВ в этом случае можно оценить следующим отношением

Э_ДИУВ= ,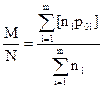

которое заведомо меньше единицы.

Нетрудно заметить, что эффективность будет почти пропорционально зависеть от элементарной вероятности p_0i, которая, в свою очередь, складывается из интенсивности ДИУВ и подверженности объектов ДИУВ.

Вышеприведенные выкладки описывают первичный эффект ДИУВ. Однако структура пространства ДИУВ зачастую носит иерархический характер, когда объекты, в которых достигнут успех ДИУВ на первичном уровне, становятся вторичными источниками ДИУВ по отношению к вторичным объектам их влияния. В этом случае вышерассмотренную модель следует далее также применить для стохастического анализа процесса ДИУВ на вторичном уровне. Если на первичном уровне матожидание составит M₁, а для каждого вторичного ДИУВ матожидание успеха составит M_j, j=1(1)M₁, то суммарное матожидание с учетом вторичного эффекта будет равно

М₂ = М₁ + .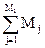

По аналогии, эффект s-порядка принесет в среднем успех в следующем количестве случаев

М_s = М_s-1 + .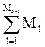

Таким образом, формируется соответствующий ряд, описывающий цепную реакцию ДИУВ.

Вторая стратегия ориентирована на многоуровневую цепную реакцию эффектов высших порядков.

Вероятностно эту ситуацию можно описать гипергеометрическим распределением

P= ,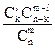

где рассматривается вероятность выявления k проблемных объектов в выборке объема m, взятой из социума объема n, который содержит l проблемных объектов. Математическое ожидание успеха ДИУВ составит в данном случае

М_Б= .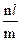

Как при первой, так для второй стратегии интерес представляет успешность ДИУВ, которое зачастую представляет собой последовательность элементарных (единичных) информационных ДИУВ. Здесь вероятность успеха после k-ой атаки будет равна

P=p₀(1-p₀)^k,

а матожидание (1-p₀)/p₀ естественно определяется элементарной вероятностью успеха от единичного ДИУВ p₀. При этом вероятность появления k успешных ДИУВ после n элементарных ДИУВ на объект может быть оценена следующим образом

P = C^k-1_n+k-1p^k₀(1-p₀)^k.

Матожидание k(1-p₀)/p₀ также зависит от p₀.

Задачу возможно детализировать далее, имея ввиду, что объекты располагают ограниченными коммуникационными возможностями. Допустим, что в пространстве из N объектов каждый из них имеет возможность передавать ДИУВ в среднем к N₀ иным объектам данного пространства. Вброс ДИУВ на первой итерации даст матожидание успеха в следующем количестве объектов

M₁=p_BN₀

или с учетом частичной нейтрализации успеха

M₁=p_BN₀(1-p_H),

где: p_B – вероятность восприятия ДИУВ единичным объектом пространства;

p_H – вероятность нейтрализации успеха ДИУВ в единичном объекте пространства.

Вторая итерация, когда объекты М₁ выступают вторичными источниками распространения ДИУВ, очевидно даст матожидание

M₂=M₁[p_BN₀(1-p_H)](1-p_H)

или с учетом того факта, что коммуникации могут быть как с уже подверженными ДИУВ объектами, так и с пока ободными от него, имеем

M₂=M₁² (1-p_H)(1- )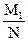

с поправкой на вероятность первичных контактов с ДИУВ.

Рассмотрим вторую стратегию в приложении к информационным технологиям неформальных организаций – вербовка адептов. Число адептов первичного уровня воздействия (первая итерация) равно

,

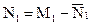где 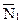- количество адептов, утративших влияние ДИУВ в результате нейтрализации мер (противодействия) и некой естественной убыли.

N₁=p_BN–p_H(p_BN)=p_BN(1-p_H)

При этом только N₁₂ из них способны выполнять роль проводников ДИУВ (вторичных источников ДИУВ) на вторичном уровне (вторая итерация)

N₁₂ = k₁₂N₁,

где k₁₂ – некий коэффициент активности адептов множества N₁. Вероятность успеха их воздействия p₀₂ зачастую бывает ниже, чем у первичного источника p₀₁, где M₁=p₀₁N.

Вторичный эффект дает нам матожидание

M₂=p₀₂(N-N₁)N₁₂.

В результате имеем

N₂=N₁+p₀₂(N-N₁)N₁₂

или

,

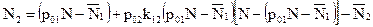где 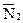- результат противодействия на вторичном уровне.

Очевидно, что в данном случае мы имеем уже уравнение второго порядка относительно N – базовой численности социума, подверженного ДИУВ, т.е.

.

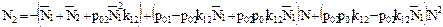Полагая 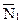= =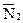0 (без учета потерь в результатах ДИУВ), получаем несколько упрощенную модель

N₂=p₀₁N+p₀₁p₀₂k₁₂N².

Рассмотрим социум с учетом ДИУВ и мер его нейтрализации, для чего введем следующие обозначения:

p_B – вероятность успеха ДИУВ на единичный объект социума;

p_Н – вероятность успешного противодействия (нейтрализации) ДИУВ в единичном объекте социума;

N – численность социума, подверженного ДИУВ и соответствующим мерам противодействия.

Отсюда количество воспринявших ДИУВ на втором уровне имеем

N₂=[N₁+N₁p_B(N-N₁)](1-p_H)=(N₁+p_BN₁N-p_BN₁²)(1-p_H)=Np_B(1-p_H)²(1+Np_Bp_H).

По аналогии на уровне (k+1)

N_k+1=[N_k+N_kp_B(N-N_k)](1-p_H),

где N_k – количество адептов, полученных в результате ДИУВ на уровне k.

По аналогии для k-ой итерации можно записать следующее выражение матожидания

,

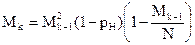где M_k-1 – матожидание (k-1)-ой итерации. Пользуясь вышеприведенными рекурсивными выражениями, можно найти матожидание успеха ДИУВ на любом этапе его распространения.

В связи с вышеизложенным уместно сделать следующие выводы:

1. При жесткой иерархии пространства и передаче ДИУВ от вышестоящего объекта к нижестоящему (отсутствии перекрестных ДИУВ) поправочный коэффициент 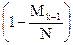может быть исключен из рассмотрения.

2. Устанавливая соотношения между M_k и N, скажем, M_k=mN, задавая тем самым степень их близости и успеха ДИУВ в пространстве N, можно получить уравнения, которые уместно разрешить из относительно p_B или p_H при заданных остальных параметрах. Параметры m и k фактически определяют эффективность ДИУВ, которая может управляться через p_B и p_H.

3. Развивая средства ДИУВ и меры противодействия, мы фактически наращиваем p_B и p_H, а рост коммуникабельности пространства (увеличение N₀) открывает перспективу для успеха ДИУВ [59].

Вопросы для самоконтроля

1. На основе теории конфликтов проведите анализ мотивов террористической деятельности.

2. Поясните специфику информационно-психологических операций и атак террористического характера.

3. На моделях покажите сущность процессов последействия информационно-психологических операций атак террористического характера.

4. Перечислите приемы кибертерроризма

5. Приведите сценарные модели информационно- психологических операций и атак террористического характера.

6. Перечислите меры противодействия информационным операциям террористического характера.

7. Проведите анализ сценариев, содержания и целей террористических информационных операций и атак.

8. Опишите вероятностные модели террористических атак.

9. Рассмотрите энтропийные модели террористических атак.

10. Приведите обобщенную модель террористической атаки социотехнической системы.

11. Опишите процессы, активизируемые терактом в информационно-психологическом пространстве социотехнической системы.

12. Дайте характеристику защищённость системы.