Тема 4. Элементы математической логики

1. Определите, какие из высказываний являются истинными, а какие – ложными:

а) 2 ∙ 2 ≥ 4;

б) Если число 8 имеет меньше четырех делителей, то оно является рациональным;

в) Натуральное число делится на 15 тогда и только тогда, когда оно делится на 5;

г) Если x ∙ y = 0, то x = 0 и y = 0.

2. Определите значения истинности высказываний A и B, если

а) (29 – рациональное число) 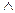A – ложное высказывание;

б) B 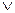(29 – иррациональное число) – истинное высказывание.

3. Определите значения истинности высказываний A и B, если

а) (6 – составное число) 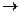A – ложное высказывание;

б) B 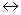(6 – простое число) – истинное высказывание.

4. Определите значения истинности высказываний A и B, если известно, что:

а) высказывание « 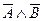» – истинное высказывание;

б) высказывание « 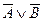» – ложное высказывание;

в) высказывание « 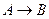» – ложное высказывание.

5. Составьте таблицу истинности для следующего высказывания: .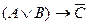

6. Определите значения истинности высказываний и постройте их отрицания:

а) квадратный корень из числа 64 равен 8;

б) некоторые натуральные числа имеют наибольшее кратное;

в) все натуральные числа нечетны;

г) число 21 не принадлежит множеству целых чисел и кратно 7;

д) число 33 является простым или не делится на 5.

7. Докажите или опровергните следующие утверждения:

а) некоторые натуральные числа имеют ровно три делителя;

б) все двузначные числа являются составными;

в) существуют трапеции, у которых углы при основании равны;

г) в любой четырехугольник можно вписать окружность.

8. Вставьте вместо многоточия одно из пропущенных слов «необходимо», «достаточно» или «необходимо и достаточно» так, чтобы получилось истинное высказывание:

а) для того, чтобы сумма чисел делилась на 5, …, чтобы каждое слагаемое делилось на 5;

б) для того, чтобы четырехугольник был квадратом, …, чтобы он был прямоугольником;

в) для того, чтобы вычитание было выполнимо на множестве натуральных чисел, …, чтобы уменьшаемое было больше вычитаемого.

9. Является ли второе предложение следствием первого предложения?

а) 1. Углы A и B вертикальные.

2. Углы A и B равны.

б) 1. a, b – иррациональные числа.

2. a∙b – иррациональное число.

10. Определите, в каком отношении находятся следующие предложения.

а) 1. Число x делится на 2.

2. Десятичная запись числа x оканчивается цифрой 0.

б) 1. Четырехугольник является ромбом.

2. Диагонали четырехугольника пересекаются и точкой пересечения делятся пополам.

11. Используя правило заключения, закончите умозаключения так, чтобы они были дедуктивными:

а) «Если треугольники равны, то они имеют равные площади. Треугольники ABC и MNK …»;

б) «Если число x делится на 9, то сумма его цифр делится на 9. Число 5742 …»

12. Используя правило отрицания, закончите умозаключения так, чтобы они были дедуктивными.

а) «Если треугольники равны, то они имеют равные площади. Треугольники ABC и MNK …»;

б) «Если число x делится на 9, то сумма его цифр делится на 9. Сумма цифр числа 3624 …»