Тема 1. Множества и операции над ними

Тема 1. Множества и операции над ними

1. Задайте двумя способами следующие множества:

а) A – множество делителей числа 24;

б) E – множество чисел, кратных 4 и меньших 28.

В каком отношении находятся данные множества?

2. B – множество натуральных чисел, больших 10, но меньших 35. Составьте подмножество множества B, в котором каждый элемент:

а) число, оканчивающееся цифрой 9;

б) число, записанное одинаковыми цифрами;

в) простое число.

Изобразите при помощи кругов Эйлера отношения между получившимися тремя множествами.

3. Выясните, в каком отношении находятся следующие множества:

а) X – множество четных чисел,

Y – множество чисел, кратных 7;

б) R – множество прямоугольных треугольников,

S – множество равносторонних треугольников;

в) C = {4, 6, 8, 9},

D – множество составных однозначных чисел;

г) T – множество прямоугольников,

Q – множество квадратов.

4. Запишите все подмножества множества F = {m, p, h, s}. Сколько всего получилось подмножеств? Какие из данных подмножеств являются собственными, а какие несобственными?

5. Изобразите при помощи кругов Эйлера отношения между множествами M, N и P, если:

а) M – множество треугольников;

N – множество равнобедренных треугольников;

P – множество тупоугольных треугольников.

б) M – множество чисел, кратных 2;

N – множество трехзначных чисел;

P – множество чисел, кратных 4.

6. Найдите пересечение, объединение и разность множеств A и B, если

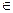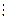A = {x / x N, x 2, x < 8}, B = {x / x 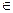N, 28 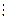x, x ≤ 7}.

7. Известно, что A – множество букв слова «цифра», B – множество букв слова «три». В каком отношении находятся данные множества? Найдите разность множеств A и B. Верно ли, что A\B = B\A?

8. Множества A, B, C попарно пересекаются. Изобразите с помощью кругов Эйлера следующее множество: B \ (A 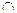C).

9. Запишите формулу, соответствующую не заштрихованной на кругах Эйлера области:

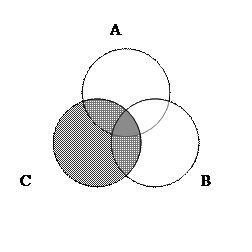
10. Известно, что A = {2, 7}, B = {3, 5, 8}. Перечислите элементы, принадлежащие декартовому произведению множеств B и A. Изобразите получившееся множество на координатной плоскости. Верно ли следующее утверждение: «Декартово умножение множеств коммутативно»?

11. На координатной плоскости построены прямые, параллельные оси oy и проходящие через точки (–2, 1) и (3, 1). Установите, декартово произведение каких двух множеств изображается в виде полосы, заключенной между построенными прямыми.

12. Решите задачу двумя способами: «Каждый ученик класса посещает либо математический кружок, либо биологический, либо оба кружка. Математический посещают 14 человек; биологический – 16 человек; оба кружка – 5 человек. Сколько учеников в классе?»

Тема 6. Системы счисления

1. Цифра десятков в записи данного двузначного числа в четыре раза больше цифры единиц. Если эти цифры переставить, то получится число, меньшее данного числа на 54. Найдите данное число.

2. На примере чисел 283 и 415 покажите, какие теоретические положения лежат в основе алгоритма сложения натуральных чисел.

3. На примере чисел 947 и 6 покажите, какие теоретические положения лежат в основе алгоритма умножения многозначного числа на однозначное число.

4. На примере чисел 793 и 152 покажите, какие теоретические положения лежат в основе алгоритма вычитания натуральных чисел.

5. Покажите на конкретном примере, как перейти от записи числа в шестеричной системе счисления к записи этого числа в десятичной системе счисления.

6. Покажите на конкретном примере, как перейти от записи числа в десятичной системе счисления к записи этого числа в пятеричной системе счисления.

Тема 1. Множества и операции над ними

1. Задайте двумя способами следующие множества:

а) A – множество делителей числа 24;

б) E – множество чисел, кратных 4 и меньших 28.

В каком отношении находятся данные множества?

2. B – множество натуральных чисел, больших 10, но меньших 35. Составьте подмножество множества B, в котором каждый элемент:

а) число, оканчивающееся цифрой 9;

б) число, записанное одинаковыми цифрами;

в) простое число.

Изобразите при помощи кругов Эйлера отношения между получившимися тремя множествами.

3. Выясните, в каком отношении находятся следующие множества:

а) X – множество четных чисел,

Y – множество чисел, кратных 7;

б) R – множество прямоугольных треугольников,

S – множество равносторонних треугольников;

в) C = {4, 6, 8, 9},

D – множество составных однозначных чисел;

г) T – множество прямоугольников,

Q – множество квадратов.

4. Запишите все подмножества множества F = {m, p, h, s}. Сколько всего получилось подмножеств? Какие из данных подмножеств являются собственными, а какие несобственными?

5. Изобразите при помощи кругов Эйлера отношения между множествами M, N и P, если:

а) M – множество треугольников;

N – множество равнобедренных треугольников;

P – множество тупоугольных треугольников.

б) M – множество чисел, кратных 2;

N – множество трехзначных чисел;

P – множество чисел, кратных 4.

6. Найдите пересечение, объединение и разность множеств A и B, если

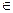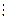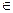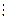A = {x / x N, x 2, x < 8}, B = {x / x N, 28 x, x ≤ 7}.

7. Известно, что A – множество букв слова «цифра», B – множество букв слова «три». В каком отношении находятся данные множества? Найдите разность множеств A и B. Верно ли, что A\B = B\A?

8. Множества A, B, C попарно пересекаются. Изобразите с помощью кругов Эйлера следующее множество: B \ (A 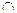C).

9. Запишите формулу, соответствующую не заштрихованной на кругах Эйлера области:

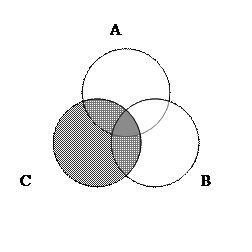
10. Известно, что A = {2, 7}, B = {3, 5, 8}. Перечислите элементы, принадлежащие декартовому произведению множеств B и A. Изобразите получившееся множество на координатной плоскости. Верно ли следующее утверждение: «Декартово умножение множеств коммутативно»?

11. На координатной плоскости построены прямые, параллельные оси oy и проходящие через точки (–2, 1) и (3, 1). Установите, декартово произведение каких двух множеств изображается в виде полосы, заключенной между построенными прямыми.

12. Решите задачу двумя способами: «Каждый ученик класса посещает либо математический кружок, либо биологический, либо оба кружка. Математический посещают 14 человек; биологический – 16 человек; оба кружка – 5 человек. Сколько учеников в классе?»