Формулы включения-исключения

Формулы включения-исключения позволяют определить число элементов в объединении нескольких конечных множеств. Рассмотрим случаи двух и трех множеств. Число элементов конечного множества будем обозначать через .

Тогда для двух конечных множеств А и В справедлива формула,

(7.1)

Справедливость этой формулы можно проиллюстрировать диаграммой Эйлера-Венна.

Действительно общее количество элементов в объединении двух множеств будет складываться из количества элементов в области А и из количества элементов в области В без двойного подсчета элементов в пересечении двух областей (заштрихованная область)

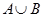Для трех конечных множеств А, В и С справедлива формула

(7.2)

Общее количество элементов в объединении трех множеств будет складываться из количества элементов в области А, из количества элементов в области и В количества элементов в области С без двойного подсчета элементов в пересечении пар областей (заштрихованная область), но с учетом области тройного наложения.

Пример 1.14.Порезультатам тестов из 25 слушателей студенческой группы 12 человек показали себя как обладатели веселого характера, 16 — проявили себя как замкнутые и 8 не показали себя ни веселыми, ни замкнутыми. Сколько человек оказались одновременно веселого, но не замкнутого характера?

Решение. Пусть А — множество студентов веселого характера, В — множество студентов замкнутого характера, и С — множество студентов не обладающих ни веселым ни замкнутым характером.

Количество студентов, которые имеют либо веселый, либо замкнутый характер, равно . Обозначим через количество студентов веселого, но не замкнутого характера, тогда . Отсюда .

Пример 1.14.В бюро переводов работают несколько человек, причем каждый из них знает хотя бы один из трех языков — английский, французский и немецкий. Английский язык знают 12 человек, французский — 10 человек, немецкий — 8 человек, английский и французский — 6 человек, английский и немецкий — 4 человека и французский и немецкий — 2 человека. Все три языка знает один человек. Сколько человек работает в бюро переводов? Сколько из них знает только английский язык? Только французский язык? Только немецкий язык?

Решение. Введем следующие множества:

А — множество всех сотрудников, знающих английский язык;

В — множество всех сотрудников, знающих французский язык;

С — множество всех сотрудников, знающих немецкий язык,

D — множество всех сотрудников, знающих английский и французский языки,

E — множество всех сотрудников, знающих английский и немецкий языки.

Из условия задачи можно записать:

, ,
, ,

Применяя формулу включения-исключения для трех множеств, получим общее число переводчиков бюро:

Продолжим вычисления:

, ,
, ,

Применим формулу включения-исключения для двух множеств получим

Итак, английский язык знают 12 человек, из них еще хотя бы один язык знают 9 человек. Поэтому только английский знают человека.

Аналогично находим, что французский язык и еще хотя бы один язык знают человек. Поэтому число сотрудников, знающих только французский равно .

Только немецкий язык знают человек.