Элементы теории графов

· Пусть 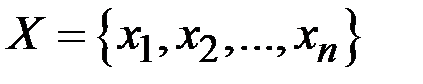– произвольное непустое множество элементов, которые называются вершинами графа (n – число вершин – порядок графа).

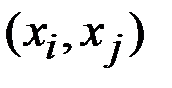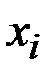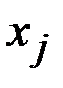· Между элементами множества Х задано соответствие, то есть некоторое множество упорядоченных пар , которые называются дугами графа, причем считается, что дуга имеет направление от до . Граф ориентированный.

· Дуга 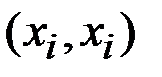называется петлей.

· Если существуют дуг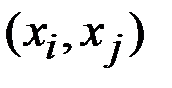и и 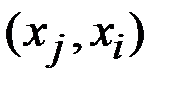, то вершины 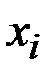и 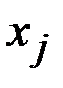соединяют линией без направления и называют ребром.(ДУГИ ИМЕЮТ НАПРАВЛЕНИЕ, РЕБРА – НЕТ)

· Последовательность дуг 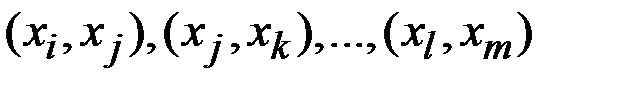, таких, что конец любой дуги (кроме последней) совпадает с началом следующей дуги, называется путем или маршрутом в графе.

· Если для пути справедливо 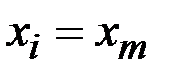, то он называется циклом.

· Граф, в котором есть хотя бы один цикл, называется циклическим. (или есть второй вариант: граф, который представляет собой цикл, называется циклическим)

· Граф, содержащий петли, называется псевдографом.

· Граф называется полным, если любые его две вершины соединены ровно одним ребром.

· Если в графе есть кратные ребра, то он называется мультиграфом.

· Граф, не содержащий циклов, петель, кратных ребер, называется ациклическим или лесом.

· Граф называется связным, если между любыми его двумя вершинами есть путь.

· Вершины 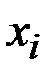и 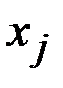называются смежными, если существует дуга или ребро 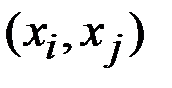или .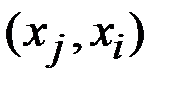

Графы можно задавать матричным способом.

· Матрица смежности – двоичная матрица (из нулей и единиц) размера n×n, в которой строкам и столбцам поставлены в соответствие вершины графа, а элементы матрицы определяются так:

· Если вершина 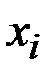является началом или концом дуги, то говорят, что данная вершина и дуга инцидентны.

· Матрица инцидентности – матрица размера n×m, показывающая какая вершина является началом, а какая является концом данной дуги (дуги нумеруются произвольным образом). Элементы определяются так:

· Степень вершины – число инцидентных этой вершине ребер (петля учитывается дважды).

· Вершина степени 0 – изолированная вершина.

· Граф называется однородным, если все вершины имеют одну и ту же степень.

· Граф называется симметричным или неориентированным, если отношение между вершинами симметрично. Если есть дуга 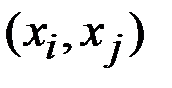, то есть дуга 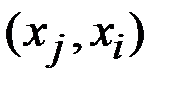. Дуги изображаются без стрелок.

· Гамильтонов цикл – замкнутый обход симметричного графа по всем его вершинам по одному разу. Эйлеров цикл – по всем ребрам по одному разу.

· Ациклический связный граф, в котором одна вершина имеет степень захода 0, а все остальные имеют степень захода 1, называется деревом. «Корень» изображают наверху, это нулевой уровень (ярус). Остальные вершины расположены ниже на первом, втором и т.д. уровнях. Число уровней – высота дерева.