Логистическаямодельдемографическогороста
Увеличениенаселенияпоэкспоненциальномузаконуможетпродолжатьсядобесконечности. Очевидно, подобнаядинамикавозможнатогда, когданикакиефакторыприродногоилисоциальногопорядканеограничиваютэтотрост. Вреальностиэкспоненциальныйростнаблюдаетсянаограниченномвременноминтервале. Поэтомуужев XIX векепроводилисьпоиски «закона», которыйбыотражалфактсдерживанияэкспоненциальногоростанаселенияпомереувеличенияегочисленности. Так, известныйбельгийскийфизикА. Кетле, опираясьнапримерыизфизики, предполагал, что «сопротивлениеростунаселениядолжновозрастатьпропорциональноквадратускоростиэтогороста». ВдальнейшембельгийскийматематикП. Ферхюльст (1838) реализовалэтугипотезувматематическойформеввидекривой, которуюонназвал «логистической». Затемегооткрытиебылопрактическипреданозабвениюдо 1920 г., когдаамериканскиеученыеР. ПирлиЛ. Ридвновьввелилогистическуюкривуювнаучныйоборотдляописанияростачисленностипопуляцийвбиологииидемографиичеловека. Математическилогистическаяфункциявыражаетсяформулой
P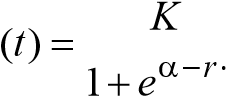 
t ,
гдеP(t) — численностьнаселениявмоментt ; e — основаниенатуральныхлогарифмов; K, α, r — параметрыуравнениялогистическойкривой.
Графическилогистическаяфунцияпредставляется в виде
S-образной, илисигмоидной, кривой
(см. рис. 16.2). ПараметрK определяетположениелинии (асимптоты), задающей
максимально воз- можнуюилипедель-
нуючисленностьнасе- Рис. 16.2 Кривая логистического роста населения
ленияприданныхусловиях. Егоможнотрактоватькакмеру «емкостисреды» дляособейданноговида. Величинаэтогопараметра, какпоказалидемографическиеисследования, например, дляСША, увеличиваетсясовременем. Подобноеувеличениепределовростаученыесвязывалисрастущейемкостьюсредыобитаниячеловекаблагодарянаучно-техническомупрогрессу.
| Вставка 16.4. Гиперболическая модель роста населения Земного шара Попыткинайтимодель, описывающуюдинамикучисленностинаселениявсейЗемлизадлительныйпериодвремени,привелинекоторыхученых, средикоторыхможноназватьизвестногофизикаакадемикаС.Капицу, кзаключению, чтодемографическиеданныезамногопоколенийхорошоукладываютсятольконагиперболическуюкривую. Наосновеанализадемографическихданныхбылаполученапростаяформула, соответствиекоторойреальнымданнымпоказанонарисунке16.3: P = C /(T1 −T) =186/(2025 −T) , гдеP — числолюдейназемлевмоментвремениT (млрд. чел.); T1 — критическаядата; C — постояннаяCсразмерностью (человеко-годы). Однакоги- 8000 перболическаямодельвызывает7000 целыйрядво- 6000 просовсреди5000 | |
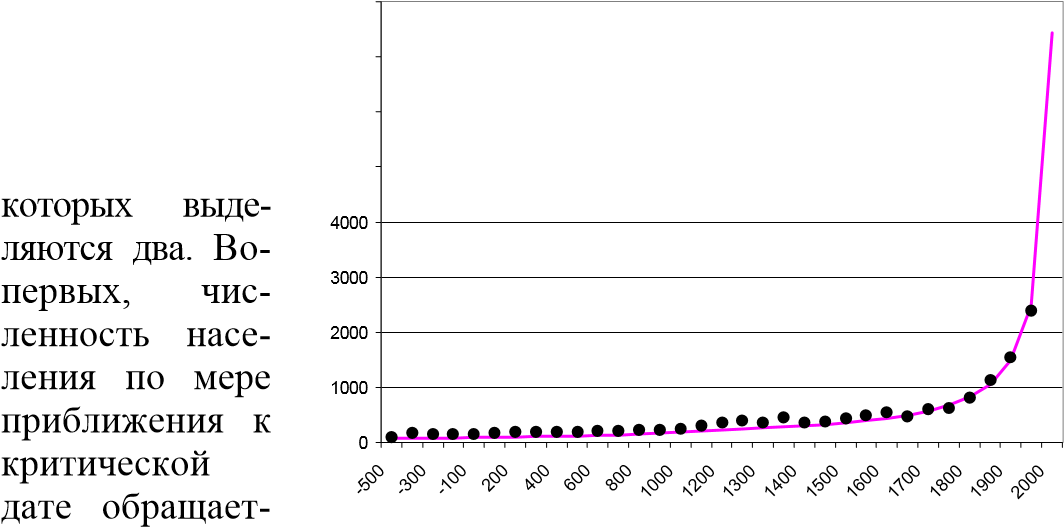 сявбесконеч- Рис. 16.3 Гиперболическая модель роста ность. Получа- (млн. чел.) ется, что 2025 годявляетсяподобиемконцасвета. Во-вторых, делиможноприйтикдругомуабсурдномурезультату, чтолюдипрошлом, например, 10 или 20 млрд. леттомуназад. ВцеляхпреодоленияэтихтрудностейС. Капицаустановил числалюдейпогиперболе, каквпрошлом, такивнастоящем. ницаопределяетсяусловием, чтоскоростьростанеможетбыть человеказапоколение. Максимальнаяграницаопределяетсяприближенияккритическойточкевсилувступаютфакторы, демографическийрост. Скоростьростачисленностинаселения оченьбольшой. Онапроходитчерезмаксимумвпериодхода. Померетого, какскоростьдемографическогоростаниеЗемливыходитнаплатоистабилизируется. Гиперболический ниячисленностинаселенияперестаетдействовать. | оценки Бюро Цензов (США) гиперболическая модель |
| населения мира согласноэтойможиливдалеком границыроста Минимальнаяграменееодноготем, чтопомереограничивающиенестановится демографическогопереуменьшается, населезаконизмене- |
ЛИТЕРАТУРА
Основная
1. КапицаС. Скольколюдейжило, живетибудетжитьнаЗемле. Очеркитеорииростачеловечества. М., 1999.
2. Курсдемографииподред. БоярскогоА.Я. М.. Дополнительная
1. КапицаС. Математическаямодельростанаселениямира // Математическоемоделирование. М., 1992. Т 4, № 6.
2. Keyfitz N. Applied Mathematical Demography. N.-Y., 1985.
3. КапицаС.П. ТеорияростанаселенияЗемли. М., 1997.