Простыемоделидемографическогороста

Простыми^[90]называютдемографическиемодели, вкоторыхспомощьюизвестныханалитическихфункций (линейные, экспоненциальные, гиперболическиеидр.) описываетсядинамикачисленностинаселениябезучетаизмененийвозрастно-половойструктурыиегодругихвнутренниххарактеристик. Простыемоделидемографическогоростанаселенияпоявилисьвдемографическойнаукев XVII веке. ВдальнейшемихиспользоваливсвоихтеоретическихисследованияхвыдающиесяматематикиидемографыЛ. Эйлер, В. БорткевичиА. Лотка.Внастоящеевремяпростыемоделиростанаселенияприменяютсядлярешениясамыхразнообразныхдемографическихиэкономическихзадач, вчастности:

– длявыполненияинтерполяционных, ретроспективныхипрогнозныхоценокчисленностивсегонаселенияиегоотдельныхгрупп;

– дляоценки демографическойситуации, на нихоснованынекоторые демографическиепоказатели;

– вкачествеэкзогенныхпредпосылоконивходятвразличныеэкономическиемодели.

ДЕМОГРАФИЧЕСКИЙРОСТСПОСТОЯННЫМ

ТЕМПОМПРИРОСТА

а) изменениенаселенияпозаконугеометрическойпрогрессии

ПустьнамизвестначисленностьнекоторогонаселениянаначалогодаP(0)итемпегоприростазагодθ_пр . Численностьэтогонаселениянаконецтекущего (илиначалоследующего) годаможноопределитьпоформуле (16.6):

P(1) = P(0)⋅(1+θ_пр) . (16.6)

Еслитемпприростаостанетсявбудущемнеизменным, томожноопределитьчисленностьнаселениявтечениевсехпоследующихлет. Общаясхемаизменениячисленностинаселениябудетвыглядетьследующимобразом:

численность населенияна:	правиловычисления
началопервогогода	P(0)
конецвторогогода	P(1) = P(0)⋅(1+ θпр)
конецтретьегогода	P(2) = P(1)⋅(1+ θпр) = P(0)⋅(1+θпр)2
конецчетвертогогода	P(3) = P(2)⋅(1+ θпр) = P(1)⋅(1+ θпр)2 = P(0)⋅(1+ θпр)3
…	…
конецгодаτ	P(τ) = P(τ−1)⋅(1+ θпр) =…= P(0)⋅(1+θпр)τ

Изпоследнеговыраженияследует, чтонапротяженииτлетчисленностьисследуемогонаселениянаконецкаждогоk–гогодабудетизменятьсяпоформуле

P(k) = P(0)⋅(1+θ_пр)^k , (16.7) т.е. по закону геометрической прогрессии. Такимобразом, геометрическаяпрогрессияявляетсямодельюизменениячисленностинаселенияспостояннымгодовымтемпомприроста.

б) экспоненциальныйдемографическийрост

Позаконугеометрическойпрогрессиичисленностьнаселенияменяет-

сядискретно, т.е. вопределеннойточкевременногопромежутка (внашемслучае — вконце каждогогода). Однаковреальнойдействительностичисленностьнаселенияизменяетсянепрерывно, т.е. вкаждойточкевременногоинтервала. Поэтомуаналитическоеописаниедемографическогоростаспомощьюнепрерывныхпроцессовболееадекватно, чемнаосноведискретных. Непрерывныманалогомгеометрическойпрогрессииявляетсяэкспоненциальнаяфункция. Такимобразом, формуланепрерывногодемографическогороставыражаетсяуравнением

P(k) = P(0)⋅e^r⋅t , (16.8)

гдеe — основаниенатуральногологарифма (e ≈ 2,718281828); r —моментальныйкоэффициентприростанаселения, являющийсяпостоянной. Есливеличинаr большенуля, точисленностьнаселенияувеличивается, еслиrменьшенуля —уменьшается, еслиrравно 0 — остаетсяпостоянной. Примеркривыхэкспоненциальногоростаприразныхзначенияхпостояннойrможноувидетьнарисунке 16.1.

Рис. 16.1. Модель экспоненциального роста населения России в 2000–2100 гг. при разных параметрахr(в млн. чел.)

Однакопрактикапоказала, чтовсегипотезыодинамикечисленности

населения, основанныенаэкспоненциальноймодели, невыдерживалипроверкипрактикойнадлительныхпериодах. Темпыдемографическогоростаменяются. Крометого, нанихвлияетдемографическийпотенциал, накопленныйвозрастнойструктурой. Применениевозможностеймоделидлявыполненияретроспективныхиперспективныхоценкокдемографическойдинамикиограниченокороткимивременнымиинтервалами. б) среднегодовые темпы прироста населения

Длясравненияскоростиувеличениячисленностинаселениявразныепопродолжительностипериодынеобходимооцениватьсреднегодовыетемпыростаиприроста населения. Восновеэтих оценоклежатпредположенияотом, чтовизучаемыймежпереписнойпериоднаселениеизменялосьпогеометрическойпрогрессииилиэкспоненциальномузакону. Изформулы (16.7) путемпростыхарифметическихпреобразованийнепосредственноопределяетсянеизвестнаявеличинаθ_пр , котораяиявляетсясреднегодовымтемпомприростанаселениязаkлет:

θ_пр = _k ^P(k) −1, (16.9)

P(0)

Еслиединицуперенестивправуючастьуравнения, томыполучим

среднегодовойтемпростанаселения: θ_р =1+θ_пр = _k ^P(k) . P(0)

Пустьтеперьнаселениеизменяетсяпоэкспоненциальномузакону. Тогдаизуравнения (16.8) среднегодовойтемпприростанаселениязаkлетравен:

r = ln(P(k)/ P(0) . (16.9)

k

16.10.ПЕРИОД УДВОЕНИЯ ЧИСЛЕННОСТИ НАСЕЛЕНИЯОдинизсамыхраспространенныхподходовкоценкесовременнойдемографическойситуациизаключаетсявоценкенастоящегочерезбудущее. Мыпредполагаем, чтопараметры «сегодняшнегодня» унаселениясохранятсяивотдаленнойперспективе. Затеманализируютсядемографическиехарактеристики, которыенаселениеприобрететвбудущем. Однимизтакихпоказателей, оценивающихнастоящеечерезбудущее, является «периодудвоениячисленностинаселения». Онизмеряетскоростьдемографическогороставременем, котороепотребуетсянекоторомунаселению, чтобыудвоитьсвоючисленностьприсохраненииданноготемпаприроста. Чемкорочеэтотпериод, тембыстреерастетнаселение. Естественно, еслиприростнаселенияимеетотрицательнуювеличину, торечьидетовременидвукратногосокращениячисленностинаселения.

Периодудвоениялегкорассчитатькакдлядискретного, такинепрерывноговременидемографическихизменений. ВпервомслучаеизформулыгеометрическойпрогрессииприусловииP(T) = 2⋅P(0) следует

2⋅P(0) = P(0)⋅(1+θ_пр)^T . Откудаполучаем, чтопериодудвоенияравен:

T = 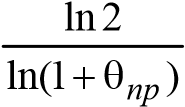. (16.11) Вовторомслучае изэкспоненциальногозаконадемографическогороставытекает 2⋅P(0) = P(0)⋅er^⋅T . Логарифмируялевуюиправуючасти, легкополучить, чтопериодудвоениядлянепрерывногослучаяравен:

T = ^ln2 . (16.12) r

Вычислениепериодаудвоениявдемографических, финансовыхиэкономическихрасчетахизвестнотакжекак «правило 70». Натуральныйлогарифм 2 равен 0,6931… илиокругленно 0,7. ТогдавнепрерывномслучаепериодудвоениябудетравенT = 0,7/rилиT = 70/(100⋅r) , есливыразитьприростнаселениявпроцентах (т.е. 100⋅r ). Вдискретномслучаедляполучения «правила 70» надозаменитьвеличину ln(1+ θ_пр) ееприближеннымзначениемθ_пр .