Определение процента текущего прироста растущих деревьев

При определении прироста у растущих деревьев в основу расчетов берется формула Пресслера (15.19):

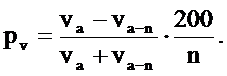
Объем дерева принимаем равным:

в данное время V_a = ghf; n лет назад V_a-n = g₁ h₁ fi.

Подставляем эти обозначения в формулу (15.19):

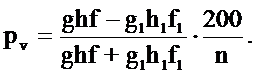
Если допустить, что за n лет высота и видовое число остались неизменными, формула, определяющая процент прироста по объему, примет следующий вид:

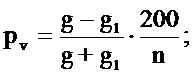g = p d² / 4, g₁ = p d₁² / 4,

отсюда

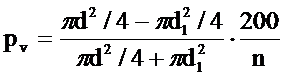
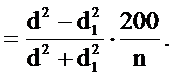
Для упрощения вычислений введем в формулу относительный диаметр.Относительным диаметром r называется частное от деления диаметра без коры d в данный момент на его прирост Z_d за n лет:

r = d / Z_d,

отсюда

d = rZ_d.

Диаметр d₁, который имело дерево год назад, обозначим через d-Z _d . В этом случае можно написать

d₁ = d -Z_d = rZ_d - Z_d (r-1).

Подставив эти величины в формулу для нахождения процента прироста по объему

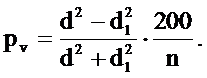
получим

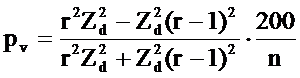
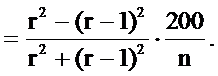
Эта формула, определяющая процент прироста по объему в зависимости от величины относительного диаметра, также предложенная проф. Пресслером, применима для деревьев, у которых прирост в высоту прекратился. Для деревьев, имеющих прирост в высоту, показатели степени в формуле должны соответственно измениться. По мере увеличения роста в высоту показатель степени также увеличивается. По опытным данным, величина его колеблется от 2 до 4.

Исходя из этого, формуле Пресслера, определяющей процент прироста по относительному диаметру, можно придать следующий общий вид:

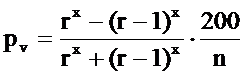
Исследования показали, что у большей части стволов показатель степени изменяется от 2 до 3,5.

Процент прироста по объему для деревьев, у которых прирост в высоту прекратился и форма осталась неизменной, определяется по формуле

p_v = p_g = 2 p_d = 200 Z_d / d

Годичный прирост по диаметру Z_d равен удвоенному приросту по радиусу 2Z_r. Отсюда получим

p_v = 200 ^. 2Z_r / d = 400 Z_r / d.

Годичный прирост по радиусу Z_r представляет не что иное, как ширину одного годичного слоя. Обозначим ее через i. Тогда формула примет такой вид:

p_v = 400 i / d. (15.25)

При определении ширины годичного слоя подсчитывают число слоев n на последнем сантиметре толщины ствола. Разделив 1 см на число слоев n, получим среднюю ширину годичного слоя 1 / n.

Подставив в формулу (15.25) вместо i величину i / n, получим следующую формулу, определяющую процент текущего прироста:

p_v = 400 / dn.

Эта формула еще в прошлом столетии была предложена немецким лесоводом Шнейдером.

Для деревьев, имеющих прирост по высоте, соответственно интенсивности этого прироста коэффициент, стоящий в числителе формулы, увеличивается. Коэффициент 400 соответствует показателю степени x в формуле (15.24), равному 2. Отсюда на единицу показателя степени приходится коэффициент 400 / 2 = 200.

При определении по выведенной формуле процента прироста для данного дерева надо на этот показатель умножить коэффициент 200. Если диаметр дерева без коры принять 38 см, а число слоев на 1 см радиуса равным 10, процент прироста по объему составит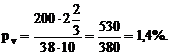

Таким образом, коэффициент, стоящий в числителе формулы, изменяется в зависимости от длины кроны и интенсивности роста в высоту. Поэтому рассмотренной формуле следует придать такой общий вид:

p_V = K_i / d, или p_V = K / dn.

При определении прироста необходимо учитывать соотношение между приростом по высоте и по диаметру. Связь этих двух величин проф. Г.М. Турский характеризует таким уравнением:

h_a-n / h_a = (d_a-n / d_a)^k.

Показатель степени k характеризует особенности роста деревьев. Если k принять равным единице, формула примет следующий вид:

h_a-n / h_a = d_a-n / d_a.

В этом случае рост дерева в высоту пропорционален росту в толщину. Такой рост называют нормальным; при нем видовое число остается неизменным и ствол во всех своих частях сохраняет в росте пропорциональность. При k=0 отношение h_a-n / h_a = 1.

Такой характер роста наблюдается у деревьев, прекративших прирост в высоту (старые деревья с отмирающей верхушкой).

Анализируя различные соотношения прироста по высоте и диаметру, можно прийти к выводу, что чем больше k, тем энергичнее рост в высоту в сравнении с ростом в толщину.

На основании уравнения находим, что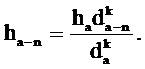

Нам известно, что процент прироста по объему может быть найден по формуле (15.19)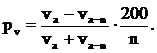

Эту формулу можно выразить следующим образом:

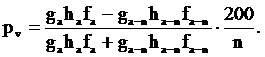
Допустим, что в течение n лет видовое число ствола остается неизменным. Тогда этой формуле можно придать такой вид:

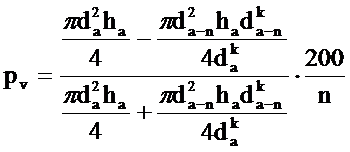
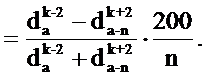
Подставив x вместо k+2, получим

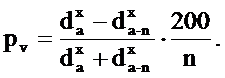
При замене абсолютных диаметров относительными выше была получена формула (15.24):

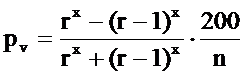
Мы уже говорили, что у большей части стволов показатель степени изменяется от 2 до 3 ¹/₃. Разделив эту амплитуду на пять частей, получаем следующие нормативы для показателя степени: 2; 2,4; 2,7; 3 и 3,3.

Основываясь на правилах сложных процентов и разложив полученные величины в ряды по биному Ньютона, в результате математических преобразований проф. Г.М. Турский получил следующую формулу для определения процента прироста по объему:

p_V = K p_d,

или

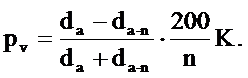
Обобщая изложенное, отметим, что точность определения прироста на срубленных деревьях зависит от точности применяемых формул. Если мы измеряем прирост на отрезках через 1-2 м, то находим прирост достаточно точно: ± 2-3%.