Определение абсолютного объемного прироста срубленных деревьев

Для нахождения абсолютного объемного прироста на срубленном дереве рекомендуется следующий простейший способ. У срубленного дерева срезают вершину. Затем на середине длины ствола измеряют диаметр без коры. В этом месте приростным буравом определяют прирост по радиусу за столько n лет, сколько слоев оказалось на торце срезанной вершины

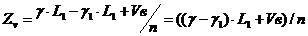Удвоив его, получают прирост по диаметру за n лет. Из величины диаметра без коры вычитают прирост по диаметру и находят диаметр n лет назад. Зная длину обезвершиненного ствола и диаметр его в настоящее время и n лет назад, можно по простой формуле срединного сечения найти объемы. Разность этих объемов, сложенная с объемом срезанной вершины и разделенная на n лет, дает текущий прирост по объему за год:

где g — площадь сечения без коры на середине

обезвершиненного ствола;

g₁ — площадь сечения ствола на середине длины n лет назад;

L₁ — длина обезвершиненного ствола;

V_B — объем вершины, которая определяет прирост по высоте

за n лет.

Объем вершины определяется по формуле объема конуса. Будучи при определении прироста за год уменьшен в 10 раз, этот объем составит ничтожно малую величину, которой можно пренебречь. Объем текущего прироста в этом случае находят по формуле:

Z_V = (g - g₁) L₁ / n.

Для более точного определения текущего прироста объем обезвершиненного ствола можно вычислять по сложной формуле срединных сечений, разметив ствол на определенное число отрезков. Подставив найденные величины в формулу (15.15), находим уточненный текущий прирост.

В таксационной практике длина отрезков l принимается за постоянную величину, устанавливаемую в 1 м, чаще всего в 2 м. При делении обезвершиненного ствола на отрезки длина последнего отрезка обычно получается несколько меньше всех остальных (1-l). Поэтому прирост всего ствола учитывается по сложной формуле: Z_V = ( g₁+g₂+ g₃+... + g_n-1 - g^/₁ - g^/₂ - g^/₃ - ... - g^/_n-1) l+(g_n-g^/_n) (l-l)+V_B.

Минимальным числом отрезков, на которые может быть размечен ствол при пользовании сложной формулой срединных сечений, будет три. В этом случае определяются диаметры без коры в данный момент и n лет назад на 1/6, 1/2 è 5/6 частях обезвершиненного ствола.

Применяемая при этом формула имеет следующий вид:

Z_V = ( g₁+g₂+ g₃ - g^/₁ - g^/₂ - g^/₃) L₁ / 3+V_B.

Прирост ствола, размеченного на двухметровые отрезки, можно определить по формуле : Z_V = ( g₁+g₂+ g₃+... + g_n - g^/₁ - g^/₂ - g^/₃ - ... - g^/_n) l / n.

Проф. А.В. Тюрин разработал метод определения текущего прироста по боковой поверхности древесного ствола без коры и ширине годичных слоев. Если площадь боковой поверхности ствола обозначить через S_ñ, а среднюю ширину годичного слоя через t, прирост по объему будет равен: Z_V = S_c t.

Для определения площади боковой поверхности ствола его делят на n равных частей. Получаемые короткие отрезки можно рассматривать как цилиндры.

Боковая поверхность каждого из этих цилиндров равна: S_ц = p d l,

где d — диаметр на середине отрезков;

l — длина этих отрезков.

Боковая поверхность всего древесного ствола будет равна

S_c = (d₁+d₂+d₃+ ... + d_n) p l + S_B,

где S_B — боковая поверхность вершины.

Площадь боковой поверхности вершины ничтожно мала, поэтому ею можно пренебречь, и формула в этом случае примет следующий вид:

S_c = (d₁+d₂+d₃+ ... + d_n) p l .

Отсюда формуле (15.16) можно придать такой вид:

Z_V = 3,14 (d₁+d₂+d₃+ ... + d_n) l t,

где t — средняя ширина годичного слоя, которую можно найти путем измерения ширины годичного слоя в разных сечениях ствола.

Вместе с тем необходимо подчеркнуть, что при определении ширины годичного слоя необходимо измерить ширину нескольких слоев (5-10) и из полученных результатов измерения вывести среднюю величину.

Формула проф. Тюрина, определяющая текущий прирост по площади боковой поверхности ствола и средней ширине годичного слоя, несколько преувеличивает величину прироста. Это объясняется тем, что последний слой у дерева наращивается на боковую поверхность, которую оно имело год назад.

Большая доля прироста по объему откладывается в нижней части ствола. Поэтому при вычислении прироста по формуле проф. Тюрина среднюю ширину годичного слоя следует выводить из результатов измерений ширины годичных слоев в нижней части ствола. Уподобляя древесный ствол цилиндру, имеющему такую же высоту, как и ствол, а основание, равное его срединному сечению, боковую поверхность ствола можно вычислить по формуле

S_c = p d L,

где d — диаметр на середине ствола; L — длина ствола.

Умножив площадь боковой поверхности на среднюю ширину годичного слоя, находят прирост по объему Z_V = p d L t.

Если необходимо точно определить прирост отдельного дерева, надо применять один из способов, основывающихся на измерениях каждого отрезка, на которые размечается древесный ствол. При учете прироста множества деревьев можно исходить из средних данных. Для получения их надо определить прирост у каждого дерева путем измерения на одном из сечений.

Возможен промежуточный способ определения прироста, при котором ствол делят на три или четыре части и для каждой из них находят боковую поверхность и ширину годичного слоя по измерениям, производимым на середине этих частей.