По двум городам известны следующие данные
| Город А | Город Б | |
| Средняя з/п | ||
| Дисперсия |
К-вар А=30% К-вар Б=25%
Как связаны между собой три вида дисперсии? Напишите формулы для каждого вида дисперсии. Что характеризует каждая дисперсия?
А) Правило сложения дисперсий
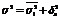, где 
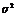- общая дисперсия, 
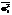- средняя из внутригрупповых дисперсий, 
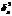- межгрупповая дисперсия
Б) Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию
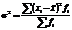
В) Межгрупповая характеризует системати-ческую вариацию.
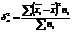где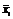 
– групповые средние; 
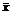- общая средняя
Г) Внутригрупповая отражает случайную вариацию
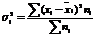где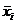 
– групповые средние
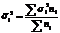где 
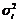– групповые дисперсии; 
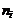- число единиц в группах
56. Стат сов-ть разбита на m групп по факторному признаку. По каждой группе известна внутригрупповая дисперсия результативного признака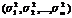 
и численность единиц в каждой группе. Как исчисляется средняя групповая дисперсия? Достаточно ли этих данных для расчета межгрупповой дисперсии?
Б) Нет, не достаточно
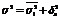, где 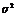- общая дисперсия, 
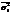- средняя из внутригрупповых дисперсий, 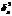- межгрупповая дисп, тк нельзя подсчитать
Стат сов-ть разбита на m групп по фак-торному признаку. По каждой группе известны внутригрупповые средние результативного признака и численность единиц в группах. Как исчисляется межгрупповая дисперсия? Достаточно ли этих данных для расчета средней внутригрупповой дисперсии? Что показывает межгрупповая дисперсия?
Б) Да, достаточно
где 
– групповые дисперсии; 
- число единиц в группах
где 
– групповые средние
При условии, что нам известен ряд вариации по группам, т.е. нам известно 
В) Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки.
Стат сов-ть разбита на m групп по факторному признаку. По каждой группе известны внутригрупповые средние результативного признака и численность единиц в группах. Достаточны ли эти данные для расчета межгрупповой дисперсии? Напишите ее формулу.
А) Достаточно, т.к. я считаю приемлемым найти общую среднюю как среднее арифм-ое групповых средних. Погрешность, естествен-но, будет, но при распределении близком к нормальному она будет минимальной. Общую среднюю можно вычислить и по выборке.
Б) 
где – групповые средние; 
- общая средняя
59. Что представляет из себя ряд дина-мики? Приведите пример интервального ряда динамики.
Ряд динамики представляет собой ряд изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке.
| Годы | ||||
| з/п 1 ч-ка |
60. Приведите примеры моментных рядов динамики с равными и неравными промежутками между датами.
РАВНЫЕ
| Годы | ||||
| з/п 1 ч-ка |
НЕРАВНЫЕ
| Годы | ||||
62. Как исчисляется средний абсолютный прирост в рядах динамики.
где 
– конечный уровень ряда динамики; n- число уровней ряда динамики
дописать цепную!!!!!!!!!!!!!!
63. Как исчисляется средний темп роста в рядах динамики.
где 
– конечный ур-нь ряда дин-ки
дописать цепную!!!!!!!!!!!!!!