Изучение формы распределения, основные типы распределений.

Приблизительное представление о форме распределения можно получить, построив график распределения (гистограмма, полигон). С увеличением числа наблюдений и умен. ширины интервалов, ломаные линии графиков сглаживаются и формируется главная кривая, кривая распределения кот. характеризует теоретическая распределения.

Изучение формы распределения вкл. решение 3-х последовательных задач:

1.выяснение общего характера распределения путем построения графика распределения.

2.подбор функции для описания подходящей эмпирического распределения.

3.проверка адекватности предлагаемого теоретического распределения эмпирическому.

Св-ва нормального распределения:

1.кривая имеет max, кот. находится в положении 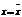, когда

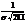
2.кривая асимптотически приближена к оси абсцисс (х).

3.симметрично относительно вертикали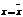

4.чем больше отличается вариант от среднего знач., тем реже встречается.

5.с измен. сред. величины кривая не меняя формы, сдвигается по оси абсцисс.

6.если принять S под кривой распределения за 1 (100%).

Чем шире диапазон, в кот. наход. случай как величина, тем выше надежность (вероятность) его нахожд., в этом диапазоне и наоборот.

Если совокупность характер. «нормал.» распределение, то правило 3-х сигм выполняется строго, поскольку из 1000 вариантов, только 3 могут не попасть. Отсюда, если совокупность распред. по нормальному закону и известно min и max знач. признака, то сред. знач. можно найти:

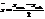
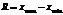
Для определения вероятности попадания случ. величины в люб. диапазон, производ. замену переменой t.

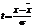
След. этапом изучения формы распред. явл. установл. адекват. прилагаемой теоретической…

Наиболее строгим и частоупотребл. явл. К. Пирсона и хи-квадрат.

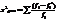
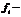эмпир. частота

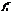- теорет.

Его расч. знач. следует сравнить с табл. кот. берут из табл. распредел., хи-квад. Пирсона, табл. знач. – это max знач., критерий хи-квадрат, при кот. можно считать что распред. соответств. закону «нормал»распределения, поэтому если табл. знач. 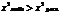, то закон выполняется. В противном случае нет.

Чтобы найти табл. знач. надо:

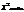df=R-3

D(1-p).

Если по каким-либо причинам табл. знач. не удается установить, то по расч. критерия и критерия согласия Романовского испол. расчетное значение хи-квадрат.

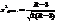, >3, закон нормал. распред. отвергается.

<3, закон принимается.

Типы распределений:

1. Распределение Пуассона.

При рассмотрении маловероятных событий, имеющих место в большойьсерии независимых испытаний некот. число раз, вероятности появления этих событий подчиняются закону Пуассона:

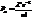
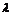равна ср. числу появления событий в одинак. незавим. испытаний, .

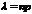Закон Пуассона модно применять для совокупностей, достаточно больших по объему (n>100) и имеющих достаточно малую долю ед. , обладающих данным признаком (Р<0,1).Распределение Пуассона подобно нормальному распределению, есть распределение, кот. оправдывает себя собственными результатами. При наличии достаточного кол-ва данных на кот. можно основать расчет среднего кол-ва случаев в пределах установленного периода времени, будет также достаточно данных для выявления фактич. кол-ва случаев в каждом из конкретных количеств однотипных периодов.

Биномиальное распределение.

Биномиальное распределение симметрично только в его ограничивающей форме. Это распределение именуется так из-за его отношения к разложению двучлена 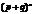. Биномиальное выражение - это выражение, кот. содержит два члена, соединенных знаком + или - . Биномиальное распределение есть распределение вероятности исходов события, кот. могут быть классифицированы как положительные или отрицательные, т.е. оно связано с обстоятельствами, в кот. какое-либо специфическое событие может случиться, или не случиться. Здесь нет места для полумер и не принимается в расчет степень интенсивности события. Общая вер-ть события, случающегося или не случающегося, равна 1.

Поэтому если вер-ть того, что оно случится, равна р, то вер-ть того, что оно не случится, равна 1-р.