Общий индекс физического объема продукции

,

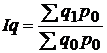где 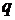– индексируемая величина;

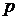– вес;

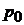– цены сопоставимые (базисные).

К индексам качественных показателей относятся индексы цен, индексы себестоимости продукции, индексы средней заработной платы, индексы производительности труда, индексы удельных расходов материалов. Эти индексы характеризуют показатели, которые носят расчетный характер. Они измеряют интенсивность, эффективность явления и являются либо средними, либо относительными величинами.

Рассмотрим расчет индивидуального и общего индекса качественных показателей на примере индекса цен.

Индивидуальный индекс цен характеризует изменение цены по каждому виду продукции:

,

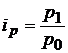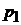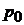где и – соответственно цена отчетного и базисного периода.

Перед общим (агрегатным) индексом качественного показателя ставится задача измерить относительное изменение уровня и абсолютную величину экономического эффекта, который получен в текущем периоде в результате этого изменения. В данном случае сумму экономии покупателей за счет снижения цен, или сумму их дополнительных расходов, если цены повысились.

Для получения общего индекса цен нужно исключить влияние изменения количества проданных товаров. Это возможно, если для обоих сравниваемых периодов использовать одинаковое количество проданных товарова, а именно: в текущем периоде, так как только на приобретении этого количества потребитель может экономить в результате снижения цен или перерасходовать в результате их повышения.

Общий индекс цен:

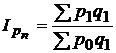– индекс цен Пааше,

где 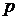– индексируемая величина; 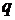– веса.

В числителе индекса дана суммарная стоимость проданных в текущем периоде товаров по ценам текущего периода, а в знаменателе – стоимость того же количества товаров, рассчитанная по ценам базисного периода.

Экономия (перерасход) от изменения цен: .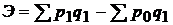

В статистике используются и другие формы представления общих индексов цен – Ласпейреса и Фишера:

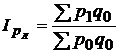– индекс цен Ласпейреса,

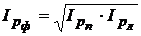– индекс цен Фишера.

Если при исчислении индексов сравниваемых периодов три и более, то возникает вопрос о выборе базы сравнения. В зависимости от базы сравнения различают цепные и базисные индексы.

Цепные индексы получают путем сопоставления индексируемого показателя любого периода с показателем предшествующего ему периода. Базисные индексы вычисляются путем сравнения индексируемого показателя каждого периода с соответствующим показателем периода, принятого за базу сравнения.

Цепные и базисные индексы могут быть как индивидуальные, так и общие.

Между цепными и базисными индексами существует определенная взаимосвязь, которая для индивидуальных индексов проявляется всегда, а для агрегатных индексов – лишь при определенных условиях.

Базисные индивидуальные индексы:

; ; .

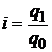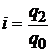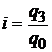Цепной индивидуальный индекс:

; ; .

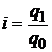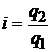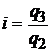Последовательное перемножение цепных индивидуальных индексов дает возможность получить базисный индекс:

.

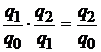Базисный агрегатный индекс физического объема продукции:

; .

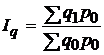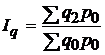Цепной агрегатный индекс физического объема продукции:

; .

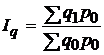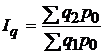Последовательно перемножение цепных агрегатных индексов физического объема продукции дает возможность получить базисный индекс:

.

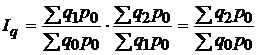Агрегатные индексы качественных показателей всегда являются индексами с переменными весами, так как при их исчислении всегда используются веса отчетного периода. Поэтому цепной метод исчисления базисных индексов для них не приемлем.

Таблица 24

Цепные и базисные индексы

Индексы	Базисные	Цепные
физического объема продукции		; ; ;	; ; ;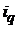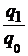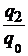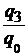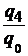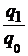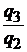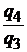
	; ; ;	; ; ;
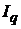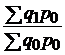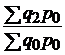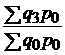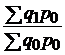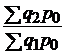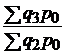цен		; ; ;	; ; ;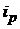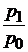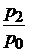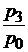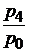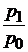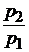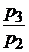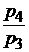
	; ;	; ;
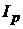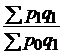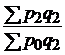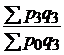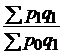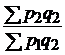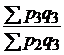стоимости		; ;	; ;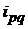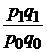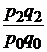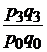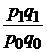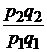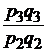
	; ;	; ;

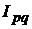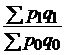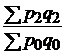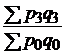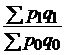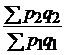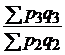3.Средние индексы и их виды.Агрегатный способ исчисления общих индексов является основным, но не единственным в статистике. В ряде случаев из-за отсутствия некоторых данных нельзя произвести расчет по формуле агрегатного индекса. Это может иметь место в том случае, если нет данных об абсолютном значении индексируемой величины, т.е. величины показателя, характеризующего ту сторону явления, изменение которой изучается (например, при исчислении индекса физического объема продукции нет данных об объеме производства в целом). В этом случае применяются средние индексы.

Мы знаем, что индивидуальный индекс физического объема выражается 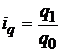, следовательно, 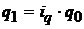. Если в формуле агрегатного индекса 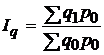заменить 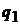на выражение 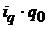, то получим формулу среднего арифметического индекса физического объема:

.

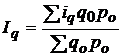Пример.

Таблица 25

Наименование товара	Изменение объема продаж в отчетном периоде по сравнению с базисным, %	Товарооборот в базисном периоде, млн.руб.
Картофель	+25
Капуста	+75
Молоко	без изменения

Определить общий индекс физического объема продукции.

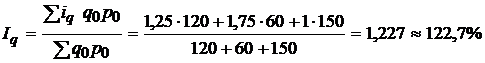(объем выпуска увеличился на 22,7%).

В тех случаях, когда нет данных о количестве проданных товаров, нельзя исчислить агрегатный индекс цен, но если известны индивидуальные индексы цен, а также имеются данные о продажах в текущем периоде в ценах текущего периода, таким образом, можно исчислить средний гармонический индекс цен.

Из формулы индивидуального индекса цен 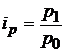, определим 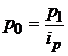. Если в агрегатном индексе цен 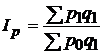заменить в знаменателе 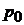на 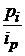, то получим формулу среднего гармонического индекса цен: .

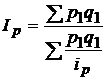Пример.

Таблица 26

Наименование товара	Изменение цены в отчетном периоде по сравнению с базисным, %	Товарооборот в текущем периоде, млн.руб.
Картофель	-25	112,5
Капуста	-17	87,5
Молоко	+17	175,0

Определить общий индекс цены:

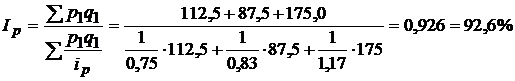
(цены снижены на 7,4%).