Основные показатели рядов динамики

При изучении динамики используются различные показатели и методы анализа, как элементарные, более простые, так и более сложные, требующие соответственно применения более сложных разделов математики.

Если каждый уровень сравнивается с предыдущим, то полученные при этом показатели называются цепными, так как они представляют собой как бы звенья «цепи», связывающей между собой уровни ряда. Если же все уровни связываются с одним и тем же уровнем, выступающим как постоянная база сравнения, то полученные при этом показатели называются базисными.

Абсолютный прирост показывает, на сколько единиц увеличился (или уменьшился) уровень по сравнению с базисным, т. е. за тот или иной промежуток (период) времени. Абсолютный прирост равен разности между сравниваемыми уровнями и измеряется в тех же единицах, что и эти уровни:

Δ =yi - yi-1;

Δ =yi - y0,

где уi – уровень i-го года; yi-1 – уровень предшествующего года; y0 – уровень базисного года. Если уровень уменьшился по сравнению с базисным, то ? ‹ 0; он характеризует абсолютное уменьшение уровня.

Абсолютный прирост за единицу времени (месяц, год) измеряет абсолютную скорость роста (или снижения) уровня. Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных приростов равна соответствующему базисному приросту, т. е. общему приросту за весь период.

Более полную характеристику роста можно получить только тогда, когда абсолютные величины дополняются относительными. Относительными показателями динамики являются темпы роста и темпы прироста, характеризующие интенсивность процесса роста.

Темп роста (Тр) – статистический показатель, который отражает интенсивность изменения уровней ряда динамики и показывает, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения – какую часть базисного уровня составляет сравниваемый уровень; измеряется отношением текущего уровня к предыдущему или базисному:

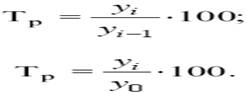
Как и другие относительные величины, темп роста может быть выражен не только в форме коэффициента (простого отношения уровней), но и в процентах. Как и абсолютные приросты, темпы роста для любых рядов динамики сами по себе являются интервальными показателями, т. е. характеризуют тот или иной промежуток (интервал) времени.

Между цепными и базисными темпами роста, выраженными в форме коэффициентов, существует определенная взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста за весь соответствующий период, например: y2/ y1 y3/ y2 = y3/ y1.

Темп прироста (Тпр) характеризует относительную величину прироста, т. е. представляет собой отношение абсолютного прироста к предыдущему или базисному уровню:

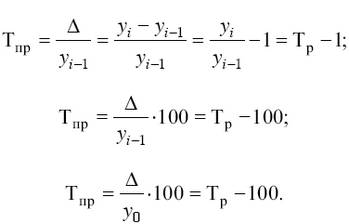
Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился (или уменьшился) уровень по сравнению с базисным, принятым за 100 %.

При анализе темпов развития никогда не следует упускать из виду, какие абсолютные величины – уровни и абсолютные приросты – скрываются за темпами роста и прироста. Нужно, в частности, иметь в виду, что при снижении (замедлении) темпов роста и прироста абсолютный прирост может возрастать.

В связи с этим важно изучать еще один показатель динамики – абсолютное значение (содержание) 1 % прироста, который определяется как результат деления абсолютного прироста на соответствующий темп прироста:

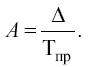
Эта величина показывает, сколько в абсолютном выражении дает каждый процент прироста.

Структура временных рядов.

В общем случае временной ряд можно разделить на составляющие его компоненты:

Основная компонента это тренд. (u)

Следующая компонента – сезонная. (s)

Циклическая компонента

Нерегулярная (случайная) компонента. (e)

Под трендом понимается устойчивое систематическое изменение процесса в течении продолжительного периода времени. На финансовых рынках различают тренд трех видов:

Возрастающий (бычий) тренд

Ниспадающий (медвежий) тренд

Боковой тренд (колебания происходят вокруг какого то среднего значения)

Для определения направленности используют слово тенденция. Это более общая характеристика, чем тренд. Тенденция среднего текущего значения является трендом.

Наряду с долговременными тенденциями во временных рядах экономических процессов часто наблюдаются более или менее регулярные колебания. Если такие колебания носят строго периодический характер и завершаются в течение одного года, то их называют сезонными колебаниями. Основной причиной, вызывающей сезонные колебания, является изменение природно-климатических условий в течение года. Сезонность также вызывают праздники, а также так называемые календарные эффекты, т.е. окончания кварталов, полугодий и т.д.

Сезонность оказывает негативное воздействие на экономические процессы, т.к. она приводит к аритмии производственных процессов.

Циклические колебания. Если период колебания составляет несколько лет, либо период колебания меньше года, то говорят о присутствии в процессе циклической компоненты. Для анализа процессов длительных колебаний нужны исходные данные за 100 лет и более.

Случайная компонента образуется из-за воздействия на экономический процесс случайных субъективных факторов. Если из исходного временного ряда правильно выделены систематические компоненты, то оставшаяся часть временного ряда и представляет собой случайные или нерегулярные компоненты. Временной ряд, составленный из значений случайной компоненты должен соответствовать ряду гипотез:

Его математическое ожидание должно приблизительно равняться нулю

Значения остаточной компоненты должны быть независимы друг от друга.

Совокупность значений остаточной компоненты должна подчиняться нормальному закону распределения.

Характеристики кривых роста

Удобным средством описания одномерных временных рядов является их выравнивание с помощью тех или иных функций времени (кривых роста). Кривая роста позволяет получить выравненные или теоретические значения уровней динамического ряда. Это те уровни, которые наблюдались бы в случае полного совпадения динамики явления с кривой.

Процедура разработки прогноза с использованием кривых роста включает в себя следующие этапы:

1) выбор одной или нескольких кривых, форма которых соответствует характеру изменения временного ряда;

2) оценка параметров выбранных кривых;

3) проверка адекватности выбранных кривых прогнозируемому процессу и окончательный выбор кривой роста;

4) расчет точечного интервального прогнозов.

В настоящее время в литературе описано несколько десятков кривых роста, многие из которых широко применяются для выравнивания экономических временных рядов.

Кривые роста условно могут быть разделены на три класса в зависимости от того, какой тип динамики развития они хорошо описывают.

К I типу относятся функции, используемые для описания процессов с монотонным характером развития и отсутствием пределов роста. Эти условия справедливы для многих экономических показателей, например, для большинства натуральных показателей промышленного производства.

Ко II классу относятся кривые, описывающие процесс, который имеет предел роста в исследуемом периоде. С такими процессами часто сталкиваются в демографии, при изучении потребностей в товарах и услугах (в расчете на душу населения), при исследовании эффективности использования ресурсов и т.д. Примерами показателей, для которых могут быть указаны пределы роста, являются среднедушевое потребление определенных продуктов питания, расход удобрений на единицу площади ит.п.

Функции, относящиеся ко II классу, называются кривыми насыщения. Если кривые насыщения имеют точки перегиба, то они относятся к III типу кривых роста к S-образным кривым.

Эти кривые описывают как бы два последовательных лавинообразных процесса (когда прирост зависит от уже достигнутого уровня): один с ускорением развития, другой - с замедлением.

S-образные кривые находят применение в демографических исследованиях, в страховых расчетах, при решении задач прогнозирования научно-технического прогресса, при определении спроса на новый вид продукции.

Вопрос о выборе кривой является основным при выравнивании ряда.

Группа кривых роста: Полиномы (многочлены) Экспоненциальные кривые S-образные кривые

Полиномы:

Полиномы первого порядка:

Yt=a_o+a₁t

Ut=Yt-Yt-1=a₁

Скорость постоянная.

Полином второго порядка:

Yt=a_o+a₁t+ a₂t²

Прирост Ut= Yt-Yt-₁= a₁- a₂t+2a₂t

Анализируя формулу для вычисления приростов можно отметить 2 особенности:

- Вычислением прироста полином более высокого порядка можно привести к полиному более низкого порядка.

- В правых частях формул для вычисления приростов отсутствует значение самой функции, т.е. приросты зависят только от времени. С экономической точки зрения это означает следующее: если дальнейшее развитие исследуемого процесса не зависит от уже достигнутого им уровня, то хорошее описание такого процесса можно получить с использованием полинома какого либо порядка.

Экспоненциальные кривые:

Их использование в отличие от полиномов наоборот предполагает, что дальнейшее развитие процесса зависит от уже достигнутого уровня.

Простая экспонента:

Y=ab^t

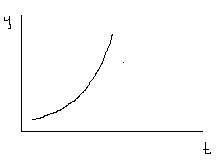
logYt=log a + t log b= a’ + b’t

Для процессов, соответствующих простой экспоненте, отношение прироста к ординате (или к функции) для каждого момента времени постоянно и равно параметру b.

Модифицированная экспонента.

Y=k+ab^t

K – асимптота, или предел насыщения, к которому стремится экспонента.

Для процессов, следующих по модифицированной экспоненте последовательное отношение приростов является постоянной величиной и равно параметру b.

S-образные кривые:

- Кривая Гомпертца

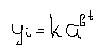
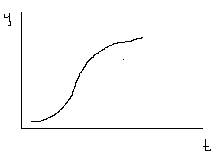
log (Ut/Yt) – линейно изменяется. (логарифм отношения прироста к функции)

- Логистическая кривая

Для логистической крвой изменяется логарифм отношения прироста к квадрату функции.

Все S-образные кривые имеют точку перегиба, до которой приросты положительны, после – отрицательны. Для логистической кривой нижняя и верхняя ветвь ее графического изображения симметричны относительно точки перегиба.

15 Производится с помощью метода наименьших квадратов.

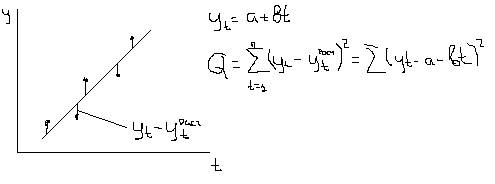
Q необходимо минимизировать.

Для этого берем частные производные по параметру a и b, приравниваем к нулю и вычисляем.

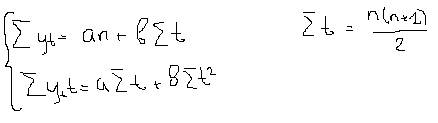
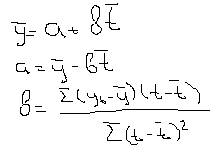
Это не подлинные параметры, а их оценки. Эти оценки обладают тремя свойствами:

1. Несмещенности

2. Состоятельности

3. Эффективности

Несмещенность означает, что математическое ожидание оценок параметра равно их истинному значению.

Состоятельность означает, что дисперсия оценок параметров стремиться к нулю при t стремящемся к бесконечности.

Эффективность означает, что оценки, вычисленные по методу наименьших квадратов имеют минимальную дисперсию по сравнению с оценками, полученными любым другим способом.

Поэтому при вычислении параметров уравнений кривых роста в первую очередь стараются использовать метод наименьших квадратов.

Метод наименьших квадратов можно использовать для вычисления параметров тех функций, в которых функция линейна относительно параметра.

Оценка параметров полинома второго порядка.

Поскольку функция линейна относительно параметра, можно применить метод наименьших квадратов, взяв три производных по трем параметрам и решив систему из трех уравнений.

Вычисление параметров простой экспоненты:

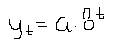
Т.к. свойство линейности относительно параметров не выполняется, то исходные уравнения путем различных преобразований стараются привести к линейному виду. Перевод уравнения из нелинейного в линейное называется линеализацией.

В данном случае процедура линеализации заключается в логарифмировании.

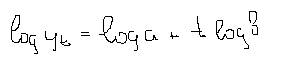
После решения системы уравнений, осуществляется потенцирование (обратный переход).

15Наиболее простой метод – визуальный, опирающийся на графическое изображение временных рядов. Подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса. Если тенденция на графике просматривается недостаточно четко, то проводят преобразование исходного ряда. В литературе описан также метод последовательных разностей (помогает в выборе кривых параболического типа).

Этот метод применяют при выполнении следующих предположений:

1. уровни ряда могут быть представлены в виде суммы трендовой составляющей и случайной компоненты, подчиненной закону нормального распределения с математическим ожиданием, равным нулю и постоянной дисперсией; метод последующих разностей предполагает вычисление первых, вторых и т.д. разностей уровней ряда:

Расчет ведется до тех пор, пока разности не будут примерно равными. Порядок разностей принимается за степень выравнивающего полинома.
Этот прием можно использовать для преобразования временного ряда.
В отдельных случаях используют метод характеристик прироста. Процедура выбора кривых роста с использованием этого метода включает:

1) выравнивание ряда по скользящей средней;

2) определение средних приростов;

3) вычисление производных характеристик прироста

Для многих видов кривых были найдены такие преобразования приростов, которые линейно изменялись относительно t или были постоянны. В связи с этим исследование рядов характеристик приростов часто оказывает существенную помощь при определении законов развития исходных временных рядов.

Данный метод является более универсальным по сравнению с методом последовательных разностей.

Однако, чаще всего на практике к выбору формы кривой подходят исходя из значений критерия, в качестве которого принимают сумму квадратов отклонений фактических значений уровня от расчетных, получаемых выравниванием. Из рассматриваемых кривых предпочтение будет отдано той, которой соответствует минимальное значение критерия, т.к. чем меньше значение критерия, тем ближе к кривой ложатся данные наблюдений.
Используя этот подход, следует иметь в виду ряд моментов. Во-первых, к ряду, состоящему из m точек можно подобрать многочлен степени (m-1), проходящий через все m точек. Кроме того, существует множество многочленов более высоких степеней, также проходящих через все эти точки. Для этих многочленов значение критерия будет равно 0, однако, очевидно, что такая кривая не слишком пригодна как для выделения тенденции, так и для целей прогнозирования.

Также следует учитывать, что за счет роста сложности кривой можно увеличить точность описания тренда в прошлом, однако доверительные интервалы при прогнозировании будут существенно шире, чем у более простых кривых при одинаковом периоде упреждения, например, за счет большего числа параметров.

Таким образом, использование этого подхода должно проходить в два этапа. На первом происходит ограничение приемлемых функций, исходя из содержательного анализа задачи. На втором - осуществляется расчет значений критерия и выбор на его основе наиболее подходящей кривой роста.

В заключение отметим, что нет “жестких” рекомендаций для выбора кривых роста. Особенно осторожно следует подходить к решению этой задачи при использовании полученной функции для экстраполирования найденных закономерностей в будущее. Применение кривых роста должно базироваться на предположении о сохранении выявленной тенденции в прогнозируемом периоде.

Для многих процессов в экономике характерно наличие связи между значениями исследуемого показателя в предпро- гнозном и прогнозном периодах. Зависимость от времени проявляется в данном случае через характеристики внутренней структуры процесса в предшествующем периоде.

Уравнение, выражающее величину переменной yt в момент t через значения этой переменной в моменты (t -\),(t ~2),...,(t-р), называется уравнением авторегрессии. В линейной форме уравнение имеет вид:

Уг = «1^-1 + «2^-2 + • • • + aPyt-P + et> (4-24)

где st - случайная составляющая с нулевым математическим ожиданием и дисперсией сг? .

Применение авторегрессионных моделей основано на предварительном экономическом анализе, когда известно, что изучаемый процесс в значительной степени зависит от его развития в прошлые периоды. В некоторых случаях они используются для нахождения простого преобразования, приводящего к последовательности независимых случайных величин.

Существует другое определение авторегрессионной модели: модель стационарного процесса, выражающего значение показателя в виде линейной комбинации конечного числа предшествующих значений этого показателя и аддитивной случайной составляющей.

В процессе анализа реальных экономических явлений понятие стационарности может быть лишь удобной абстракцией для применения статистических моделей.

Количество уровней, включенных в правую часть уравнения авторегрессии, определяет порядок уравнения.

Для предварительного изучения особенностей автокорреляционного взаимодействия элементов ряда целесообразно проводить графический анализ исходных данных путем нанесения на координатные поля пар значений (У,,У,-МУ{>У{-2\->(У,,У,-Р)- Интервалы времени (t,i -k),k = 1,2,3,...,р, характеризующие удаленность сопоставляемых уровней ряда друг от друга, называются периодом запаздывания. Он показывает, через какой промежуток времени изменение переменной yt_k окажет воздей- ствие на yt. Изучение графических построений для различных к позволяет приближенно оценить направление и силу связи между близлежащими членами ряда.

Для оценки тесноты связи используется коэффициент автокорреляции, определяемый по формуле:

ск

г к=-*-, где

со

2 п-к ^ п

П t=1 п t=l

Определив гк для нескольких интервалов запаздывания в диапазоне 1 < к < п / 4 , можно получить так называемую автокорреляционную функцию, показывающую, как изменяется коэффициент автокорреляции по мере увеличения расстояния между сопоставляемыми уровнями временного ряда.

Автокорреляционная функция характеризуется тенденцией к затуханию колебаний, т.е. уменьшению абсолютной величины коэффициента. Вследствие этого для ее анализа используются такие характеристики, как период колебаний, частота колебаний, амплитуда колебаний, фаза, т.е угловая величина отклонения автокорреляционной функции от нулевого состояния.

Оценка параметров уравнений авторегрессии выполняется методом наименьших квадратов. Прогнозирование на основе авторегрессионной модели представляет многоэтапную процедуру, каждая стадия которой позволяет определить величину показателя на очередной единичный отрезок времени.

В качестве простейшего критерия адекватности уравнения авторегрессии исходному временному ряду может использоваться показатель абсолютного среднего отклонения, определяемый по формуле:

Z к-яI

= . , . (4.25)

n-p-l + l

Сферой применения моделей авторегрессии является моделирование спроса на предметы текущего потребления, изменение складских запасов и другие составляющие логистических процессов.